题意:我们把一个城市考虑为一个图, 街道为边, 路口为点, 路口标记为 0~N-1. 盗贼从一个点开始逃亡, 每一分钟走一条边。不幸的是, 我们并不知道他逃往何处, 只能假设他每分钟都必须沿着一条边走, 不能停留但是可以反复经过。警官想要知道是否存在一个时刻, 盗贼可能出现在城市中的任意路口。
分析:给定一个无向图,从起点开始,单位时间内只能从一个边移动到相邻的点上,问是否存在一个时刻,可能出现在地图上的任意位置。
假设存在这样的时刻,那么图需要满足什么情况?
- 连通:可以使用dfs/bfs/并查集解决
- 不是二分图::可以使用dfs/bfs解决
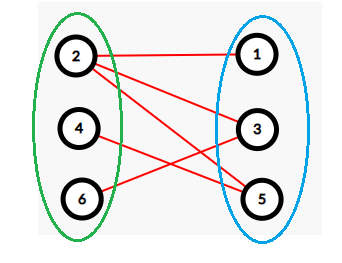
二分图定义:节点由两个集合组成,且两个集合内部没有边的图。
二分图的判定:
由二分图的定义可知,二分图有着这样一个性质:
二分图不存在长度为奇数的环,都是偶环。
因为每一条边都是从一个集合走到另一个集合,只有走偶数次才可能回到同一个集合。
这条性质将被用来判定一个无向图是否是二分图。
我们通常使用染色法判定二分图,将每个顶点染色,并且相邻的顶点染不同颜色,如果存在俩相邻点染上了同一颜色,则与二分图定义不符。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
vector<int> G[N];
int n, m, f[N];
int find(int u) {
return u == f[u] ? u : f[u] = find(f[u]);
}
// 判断连通
bool st[N];
bool bfs(int s) {
memset(st, 0, sizeof(st));
queue<int> q; q.push(s), st[s] = 1;
int tt = 1;
while (q.size()) {
auto u = q.front(); q.pop();
for (auto v : G[u]) {
if (!st[v]) {
q.push(v), st[v] = 1, tt++;
}
}
}
return tt == n;
}
// 判断二分图
int col[N];
bool dfs(int u, int c) {
col[u] = c;
for (auto v : G[u]) {
if (col[v] == c) return 0;
if (!col[v] && !dfs(v, 3 - c)) return 0;
}
return 1;
}
int main() {
int t, s, u, v, cs = 0;
scanf("%d", &t);
while (t--) {
scanf("%d%d%d", &n, &m, &s);
for (int i = 0; i < n; i++) f[i] = i;
while (m--) {
scanf("%d%d", &u, &v);
G[u].push_back(v), G[v].push_back(u);
int fu = find(u), fv = find(v);
if (fu != fv) f[fu] = fv;
}
int tt = 0;
for (int i = 0; i < n; i++)
if (f[i] == i) tt++;
// printf("Case %d: %s\n", ++cs, tt == 1 && !dfs(s, 1) ? "YES" : "NO");
printf("Case %d: %s\n", ++cs, bfs(s) && !dfs(s, 1) ? "YES" : "NO");
for (int i = 0; i < n; i++) G[i].clear();
memset(col, 0, sizeof(col));
}
return 0;
}