526互联

CodeChef Starters 83 Division 1 解题报告

发布时间 2023-04-15 16:18:34作者: DaiRuiChen007

CodeChef Starters 83 Division 1 题解

\(\newcommand \v \mathrm\)

\(\text{By DaiRuiChen007}\)

Contest Link

A. Construct String

Problem Link

题目大意

给定长度为 \(n\) 的字符串 \(S\)，每次操作可以把三个相同的字符变成一个同样的字符（\(\texttt {ccc}\to\texttt c\)）

求若干次操作后可以得到最短的 \(S\)

数据范围：\(n\le 10^6\)

思路分析

容易证明贪心地把 \(S\) 中每三个连续的相同字符都操作直到不能操作位置的策略是最优的

用一个栈模拟这个过程即可

时间复杂度 \(\mathcal O(n)\)

代码呈现

#include<bits/stdc++.h>
using namespace std;
inline void solve() {
	int n; string s,t;
	cin>>n>>s;
	for(int i=0;i<n;++i) {
		int x=t.length();
		if(x<2) t+=s[i];
		else if(t[x-1]==s[i]&&t[x-2]==s[i]) t.pop_back();
		else t+=s[i];
	}
	cout<<t<<"\n";
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int T;
	cin>>T;
	while(T--) solve();
	return 0;
}


B. Order by XOR

Problem Link

题目大意

给三个不同的非负整数数 \(a,b,c\in[0,V]\)，求出某个 \(x\in [0,V]\) 使得 \(a\oplus x<b\oplus x<c\oplus x\)，无解输出 \(-1\)

数据范围：\(V=2^{30}-1\)

思路分析

从高位到低位逐位考虑，对于当前位 \(k\)：

  • \(a_k=b_k=c_k\)：\(x_k=0/1\) 均无影响
  • \(a_k=b_k\ne c_k\)：贪心可以证明取 \(x_k=b_k\) 更优
  • \(a_k\ne b_k=c_k\)：贪心可以证明取 \(x_k=a_k\) 更优
  • \(a_k\ne b_k\ne c_k,a_k=c_k\)：
    • 若之前所有位 \(a\oplus x,b\oplus x,c\oplus x\) 都相等，则无解
    • 若 \(a\oplus x<b\oplus x\) 已被满足，取 \(x_k=b_k\) 即可得到答案
    • 若 \(b\oplus x<c\oplus x\) 已被满足，去 \(x_k=a_k\) 即可得到答案

根据上述分类讨论模拟即可

时间复杂度 \(\mathcal O(\log V)\)

代码呈现

#include<bits/stdc++.h>
using namespace std;
inline void solve() {
	int a,b,c,ans=0;
	scanf("%d%d%d",&a,&b,&c);
	auto dig=[&](int x,int k) { return (x>>k)&1; };
	int opt=0;
	for(int k=30;k>=0;--k) {
		int x=dig(a,k),y=dig(b,k),z=dig(c,k);
		if(x==y&&y==z) continue;
		if(x==y) ans|=y<<k,opt|=1;
		if(y==z) ans|=x<<k,opt|=2;
		if(x==z) {
			if(opt==0) { puts("-1"); return ; }
			if(opt==1) ans|=x<<k,opt|=2;
			if(opt==2) ans|=y<<k,opt|=1;
		}
		if(opt==3) { printf("%d\n",ans); return ; }
	}
	puts("-1");
}
signed main() {
	int T;
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}


C. Rotate to Minimum

Problem Link

题目大意

对于一个长度为 \(n\) 的字符串 \(S\) 可以进行如下两种操作：

  1. 对于某个 \(S_i\) 使 \(S_i\gets S_i+1\)（\(\texttt c\to \texttt d,\texttt z\to \texttt a\)）
  2. 对于某个 \(S_i\) 是 \(S_i\gets S_i-1\)（\(\texttt d\to \texttt c,\texttt a\to \texttt z\)）

操作 1 不超过 \(p\) 次，操作 2 不超过 \(q\) 次，求最终 \(S\) 最小可能的字典序

数据范围：\(n\le 2\times 10^5\)

思路分析

显然先将 \(S\) 的一段前缀中尽可能多的字符复原成 \(\texttt a\)

再求出最长全 \(\texttt a\) 前缀后的步骤是 trivial 的：全 \(\texttt a\) 前缀的下一个字符用 2 操作最小化字典序，剩下的能用操作 1 变成 \(\texttt a\) 就用，否则不用

考虑二分最大的 \(\texttt a\) 的前缀长度 \(len\)，对于前 \(len\) 个位置，我们需要确定用哪种操作复原，并使得两种操作的总次数分别不超过 \(p,q\)

注意到，当 \(S_i\ne \texttt a\) 时，操作 1 的花费越大，操作 2 的花费越小，反之亦然，因此可以证明最优策略一定是取用操作 1 复原代价最小的若干位置，剩下的选用操作 2，因此一遍排序即可完成判定

然后还有一个细节需要简单贪心处理，因为我们要尽可能最小化 \(S_{len+1}\)，因此在 \(S[1\dots len]\) 的复原中，应尽可能多选用操作 1，剩下按上述过程贪心即可

时间复杂度 \(\mathcal O(n\log^2n)\)

代码呈现

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+1;
char str[MAXN];
inline void solve() {
	int n,u,d;
	scanf("%d%d%d%s",&n,&u,&d,str+1);
	int l=1,r=n,res=0;
	while(l<=r) {
		auto check=[&](int x) -> bool {
			vector <pair<int,int>> v;
			for(int i=1;i<=x;++i) v.push_back(make_pair((26-(str[i]-'a'))%26,str[i]-'a'));
			int p=0,q=0;
			sort(v.begin(),v.end());
			for(auto t:v) {
				if(t.first+p<=u) p+=t.first;
				else q+=t.second;
			}
			return p<=u&&q<=d;
		};
		int mid=(l+r)>>1;
		if(check(mid)) res=mid,l=mid+1;
		else r=mid-1;
	}
	vector <pair<int,int>> v;
	for(int i=1;i<=res;++i) {
		v.push_back(make_pair((26-(str[i]-'a'))%26,str[i]-'a'));
		str[i]='a';
	}
	sort(v.begin(),v.end());
	for(auto t:v) {
		if(t.first<=u) u-=t.first;
		else d-=t.second;
	}
	if(res<n) str[res+1]-=d;
	for(int i=res+2;i<=n;++i) {
		int x=(26-(str[i]-'a'))%26;
		if(u>=x) str[i]='a',u-=x;
	}
	printf("%s\n",str+1);
}
signed main() {
	int T;
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}


D. Saber Slays

Problem Link

题目大意

你需要进行若干次“挑战”，设你的能力值为 \(u\)，对手的能力值为 \(v\)，那么每次“挑战”会发生如下 \(3\) 种结果之一：

  • \(u<v\)：你失败
  • \(u=v\)：你胜利，且 \(u\gets u-1\)
  • \(u>v\)：你胜利

给定 \(n\) 个对手，第 \(i\) 个对手的能力值为 \(s_i\)，\(q\) 次询问 \(l,r\)，你需要回答如果你想依次战胜编号为 \(l,l+1,\dots ,r\) 的对手，你的初始能力值至少是多少

数据范围：\(n,q\le 5\times 10^5\)

思路分析

考虑用线段树维护每个区间对应的信息 \((\v{in},\v{out})\)，表示想要战胜这个区间中的所有人，初始能力值至少是 \(\v{in}\)，且最终你的能力值会变成 \(\v{out}\)，一个显然的观察是对于某个区间 \([l,r]\)，其 \(\v{in}\in\{\max[s_l\sim s_r],\max[s_l\sim s_r]+1\}\)

考虑合并左右区间信息 \((L_\v{in},L_\v{out}),(R_\v{in},R_\v{out})\) 的过程

  • 若 \(L_\v{out}>R_\v{in}\)：此时直接从 \(L_\v{in}\) 进入，得到 \(L_\v{out}\) 后在右区间一定有 \(L_\v{out}>R_\max\)，因此最终的结果是 \((L_\v{in},L_\v{out})\)
  • 若 \(L_{\v out}=R_\v{in}\)：此时直接从 \(L_\v{in}\) 进入，得到 \(L_\v{out}=R_\v{in}\) 恰好可以通过右区间并得到 \(R_\v{out}\)，因此最终的结果是 \((L_\v{in},R_\v{out})\)
  • 若 \(L_\v{out}<R_\v{in}\)：
    • 若 \(R_\v{in}>L_\v{in}\)，此时直接用 \(R_\v{in}\) 进入，在左区间一定有 \(L_\max<R_\v{in}\)，可以直接到右区间，因此最终的结果是 \((R_\v{in},R_\v{out})\)
    • 否则说明 \(L_\v{in}=L_\max=(L+R)_{\max}\)，此时 \(L_\v{in}\) 无法通过，选择用 \(L_\v{in}+1\) 进入，最终的结果是 \((L_\v{in}+1,L_\v{in}+1)\)

用线段树维护上述信息的合并即可

时间复杂度 \(\mathcal O((n+q)\log n)\)

代码呈现

#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+1,INF=2e9;
struct Data {
	int in,out;
	Data(): in(INF),out(INF) {}
	Data(int x): in(x),out(x-1) {}
	Data(int _i,int _o): in(_i),out(_o) {}
	inline friend Data operator +(const Data &L,const Data &R) {
		if(L.out>R.in) return Data(L.in,L.out);
		else if(L.out==R.in) return Data(L.in,R.out);
		else {
			if(L.in<R.in) return Data(R.in,R.out);
			else return Data(L.in+1,L.in+1);
		}
	}
};
int n,q,a[MAXN];
class SegmentTree {
	private:
		struct Node {
			Data data;
		} tree[MAXN<<2];
		inline int left(int x) { return x<<1; }
		inline int right(int x) { return x<<1|1; }
		inline void pushup(int pos) {
			tree[pos].data=tree[left(pos)].data+tree[right(pos)].data;
		}
	public:
		inline void Build(int l=1,int r=n,int pos=1) {
			if(l==r) { tree[pos].data=Data(a[l]); return ; }
			int mid=(l+r)>>1;
			Build(l,mid,left(pos));
			Build(mid+1,r,right(pos));
			pushup(pos);
		}
		inline Data Query(int ul,int ur,int l=1,int r=n,int pos=1) {
			if(ul<=l&&r<=ur) return tree[pos].data;
			int mid=(l+r)>>1;
			if(ur<=mid) return Query(ul,ur,l,mid,left(pos));
			if(mid<ul) return Query(ul,ur,mid+1,r,right(pos));
			return Query(ul,ur,l,mid,left(pos))+Query(ul,ur,mid+1,r,right(pos));
		}
}	S;
inline void solve() {
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	S.Build();
	while(q--) {
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",S.Query(l,r).in);
	}
}
signed main() {
	int T;
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}


E. Restoration

Problem Link

题目大意

交互器有一个大小为 \(n\) 的排列 \(p_i\)，每次交互你可以询问一个大小为 \(n\) 的排列，交互器会返回排列 \(r_i=p_{q_i}\) 中所有Local Max（前缀最大值）的位置（即所有满足 \(\forall 1\le j<i\) 均有 \(r_j<r_i\) 的 \(i\)）

你需要在 \(n-1\) 次询问内还原排列 \(p_i\)

数据范围：\(n\le 500\)

思路分析

考虑从排列的 Local Max 入手，注意到最后一个 Local Max 一定是 \(n\)，因此不管我们第一次询问的 \(q\) 是什么，我们总能确定 \(n\) 的位置

接下来考虑 \(n-1\) 的位置，用类似的方法找倒数二个 Local Max，为了保证 \(n-1\) 不被 \(n\) 挡住，我们可以通过选择合适的 \(q\) 使得 \(r_n=n\)，然后找倒数第二个 Local Max 即可，同理可以以一次询问的代价分别确定 \(n-2,n-3,\dots ,1\) 的对应位置

注意到当已经确定 \(2\sim n\) 的位置时，\(1\) 的位置也可以求出，因此可以做到 \(n-1\) 次询问还原 \(p_i\)

时间复杂度 \(\mathcal O(n^2)\)

代码呈现

#include<bits/stdc++.h>
using namespace std;
inline void solve() {
	int n;
	cin>>n;
	vector <int> p(n+1),idx(n+1);
	for(int i=n;i>1;--i) {
		vector <int> q(n+1,0),vis(n+1,0);
		for(int j=i+1;j<=n;++j) q[j]=idx[j],vis[q[j]]=1;
		for(int j=1;j<=i;++j) {
			for(int k=q[j-1]+1;k<=n;++k) if(!vis[k]) { q[j]=k,vis[k]=true; break; }
		}
		cout<<"? ";
		for(int j=1;j<=n;++j) cout<<q[j]<<" ";
		cout<<endl;
		int s; cin>>s; vector <int> v(s);
		for(int j=0;j<s;++j) cin>>v[j];
		for(int j=0;j<s;++j) {
			if(v[j]<=i) idx[i]=q[v[j]];
		}
		p[idx[i]]=i;
	}
	for(int i=1;i<=n;++i) if(!p[i]) p[i]=1;
	cout<<"! ";
	for(int i=1;i<=n;++i) cout<<p[i]<<" ";
	cout<<endl;
	int ans; cin>>ans; 
}
signed main() {
	int T;
	cin>>T;
	while(T--) solve();
	return 0;
}


F. Mex Segments

Problem Link

题目大意

给定一个 \(0\sim n-1\) 的排列 \(a_i\)，\(q\) 次询问，每次询问给定 \(l,r,s,t\)，你需要回答有多少 \(1\le x\le y\le n\) 使得 \(l\le y-x+1\le r\) 且 \(s\le\v{mex}(a_x,a_{x+1},\dots,a_y)\le t\)

数据范围：\(n,q\le 10^6\)

思路分析

考虑当我们强制选择了 \(0\sim k-1\) 号元素，此时对 \(x,y\) 的限制形如 \(x\le u\le v\le y\)，那么我们可以得到有多少区间 \([x,y]\) 满足 \(\v{mex}(a_x,a_{x+1},\dots,a_y)\ge k\)，因此考虑用后缀和把答案拆成 \(\v{mex}(a_x,a_{x+1},\dots,a_y)\ge s\) 和 \(\v{mex}(a_x,a_{x+1},\dots,a_y)\ge t+1\) 两个询问

离线后我们每次加入 \(k\) 所在的位置，更新对应的 \([u,v]\)，然后再对区间长度用前缀和拆分，长度 \(\le x\) 的区间共有 \(\sum_{i=v-u+1}^x \min(u,n-x+1)-\max(v-x+1,1)+1\) 个，分别分类讨论拆开 \(\min\) 和 \(\max\) 即可

时间复杂度 \(\mathcal O(n+q)\)

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct Query {
	int l,r,id,c;
	Query(int _l=0,int _r=0,int _id=0,int _c=0): l(_l),r(_r),id(_id),c(_c) {}
};
inline void solve() {
	int n,q;
	scanf("%lld%lld",&n,&q);
	vector <int> a(n+1),pos(n+1),ans(q+1);
	vector <vector<Query>> Q(n+1);
	for(int i=1;i<=n;++i) scanf("%lld",&a[i]),pos[a[i]]=i;
	auto sum=[&](int l,int r) { return (l+r)*(r-l+1)/2; };
	for(int i=1;i<=q;++i) {
		int l,r,lo,hi;
		scanf("%lld%lld%lld%lld",&l,&r,&lo,&hi);
		if(lo>0) Q[lo-1].push_back(Query(l,r,i,1));
		else ans[i]+=sum(n-r+1,n-l+1);
		if(hi<n) Q[hi].push_back(Query(l,r,i,-1));
	}
	int lb=pos[0],rb=pos[0];
	for(int i=0;i<n;++i) {
		lb=min(lb,pos[i]),rb=max(rb,pos[i]);
		int len=rb-lb+1;
		auto calc=[&](int x) -> int {
			if(x<rb-lb+1) return 0;
			int ans=x-len+1;
			if(x<=n-lb+1) ans+=lb*(x-len+1);
			else ans+=lb*(n-rb+1)+sum(n-x+1,lb-1);
			if(x<=rb) ans-=sum(rb-x+1,lb);
			else ans-=sum(1,lb)+(x-rb);
			return ans;
		};
		for(auto x:Q[i]) {
			ans[x.id]+=x.c*(calc(x.r)-calc(x.l-1));
		}
	}
	for(int i=1;i<=q;++i) printf("%lld\n",ans[i]);
}
signed main() {
	int T;
	scanf("%lld",&T);
	while(T--) solve();
	return 0;
}


G. Beauty Sum

Problem Link

题目大意

给定一棵大小为 \(n\) 的树，点有点权 \(a_i\)，记 \(\v{path}(u,v)\) 为树上 \(u\to v\) 的简单路径所经过的节点集合

求 \(\sum_{1\le u<v\le n}\min\{a_i\mid i\in\v{path}(u,v\}\times\max\{a_i\mid i\in\v{path}(u,v)\}\)，即所有路径 \(u\to v\) 上最大值与最小值乘积的和

数据范围：\(n\le 2\times 10^5\)

思路分析

考虑点分治，设 \(x_i,y_i\) 分别表示节点 \(i\) 到当前分支中心 \(\v{root}\) 路径上的最小值和最大值，那么此时经过 \(\v{root}\) 的路径对答案的贡献就是 \(\sum_{u,v}[\v{subtree}(u)\ne \v{subtree}(v)]\times \min(x_u,x_v)\times\max(y_u,y_v)\)（\(\v{subtree}(u)\) 表示 \(u\) 在 \(\v{root}\) 的哪棵子树中）

但是这个式子实际上是在对三元组 \((\v{subtree}(u),x_u,y_u)\) 求三维偏序，直接求是 \(\mathcal O(n\log^2n)\) 的，加上点分治后复杂度达到 \(\mathcal O(n\log^3n)\)，无法通过此题

考虑我们在点分树统计答案时所用的容斥技巧，将 \(\v{root}\) 对答案的贡献重新表示成 \(\sum_{u,v}\min(x_u,x_v)\times\max(y_u,y_v)-\sum_{u,v}[\v{subtree}(u)= \v{subtree}(v)]\times \min(x_u,x_v)\times\max(y_u,y_v)\)

注意到第二个式子只需要对每个子树中分别求出 \(\sum_{u,v}\min(x_u,x_v)\times\max(y_u,y_v)\) 即可，而这个式子可以看成 \((x_u,y_u)\) 的二维偏序问题，用 CDQ 分治套双指针即可在 \(\mathcal O(n\log n)\) 的时间复杂度内解决（也可以使用平衡树或树状数组维护点的坐标，复杂度相同）

时间复杂度 \(\mathcal O(n\log^2n)\)

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e5+1,MOD=1e9+7;
vector <int> G[MAXN];
int ans=0;
int a[MAXN],siz[MAXN],cur[MAXN];
int mindis[MAXN],maxdis[MAXN];
bool vis[MAXN];
struct Point {
	int x,y;
	Point(int _x=0,int _y=0): x(_x),y(_y) {}
}	P[MAXN];
int pre[MAXN],suf[MAXN];
inline void calc(int p) {
	auto solve=[&](const vector <int> &ver) -> int {
		int n=ver.size(),ans=0;
		for(int i=1;i<=n;++i) P[i]=Point(mindis[ver[i-1]],maxdis[ver[i-1]]);
		sort(P+1,P+n+1,[](Point u,Point v){ return u.x<v.x; });
		auto CDQ=[&](auto self,int l,int r) -> void {
			if(l==r) return ;
			int mid=(l+r)>>1;
			self(self,l,mid),self(self,mid+1,r);
			pre[l]=P[l].x%MOD; //prefix-sum of x
			for(int i=l+1;i<=mid;++i) pre[i]=(pre[i-1]+P[i].x)%MOD; 
			suf[mid]=P[mid].x*P[mid].y%MOD; //suffix-sum of x*y
			for(int i=mid-1;i>=l;--i) suf[i]=(suf[i+1]+P[i].x*P[i].y%MOD)%MOD;
			
			pre[mid+1]=1; //prefix-sum of 1
			for(int i=mid+2;i<=r;++i) pre[i]=(pre[i-1]+1)%MOD;
			suf[r]=P[r].y; //suffix-sum of y
			for(int i=r-1;i>=mid+1;--i) suf[i]=(suf[i+1]+P[i].y)%MOD;
			
			for(int lp=l,rp=mid;lp<=mid;++lp) {
				while(rp<r&&P[rp+1].y<=P[lp].y)  ++rp;
				if(mid+1<=rp) ans=(ans+P[lp].x*P[lp].y%MOD*pre[rp]%MOD)%MOD;
				if(rp+1<=r) ans=(ans+P[lp].x*suf[rp+1]%MOD)%MOD;
			}
			for(int rp=mid+1,lp=l-1;rp<=r;++rp) {
				while(lp<mid&&P[lp+1].y<=P[rp].y) ++lp;
				if(l<=lp) ans=(ans+P[rp].y*pre[lp]%MOD)%MOD;
				if(lp+1<=mid) ans=(ans+suf[lp+1])%MOD;
			}
			inplace_merge(P+l,P+mid+1,P+r+1,[](Point u,Point v){ return u.y<v.y; });
		};
		CDQ(CDQ,1,n);
		return ans;
	};
	mindis[p]=maxdis[p]=a[p];
	vector <int> ver{p};
	for(int v:G[p]) {
		if(vis[v]) continue;
		vector <int> subt;
		auto dfs=[&](auto self,int p,int fa) -> void {
			ver.push_back(p),subt.push_back(p);
			mindis[p]=min(mindis[fa],a[p]);
			maxdis[p]=max(maxdis[fa],a[p]);
			for(int v:G[p]) {
				if(vis[v]||v==fa) continue;
				self(self,v,p);
			}
		};
		dfs(dfs,v,p);
		ans=(ans+MOD-solve(subt))%MOD;
	}
	ans=(ans+solve(ver))%MOD;
}
inline void dfs(int p) {
	calc(p); vis[p]=true;
	for(int v:G[p]) {
		if(vis[v]) continue;
		int tot=siz[v],rt=0;
		auto get=[&](auto self,int p,int fa) -> void {
			cur[p]=0,siz[p]=1;
			for(int v:G[p]) {
				if(vis[v]||v==fa) continue;
				self(self,v,p);
				cur[p]=max(cur[p],siz[v]);
				siz[p]+=siz[v];
			}
			cur[p]=max(cur[p],tot-siz[p]);
			if(!rt||cur[p]<cur[rt]) rt=p;
		};
		get(get,v,p);
		dfs(rt);
	}
}
inline void solve() {
	int n;
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) scanf("%lld",&a[i]),vis[i]=false,G[i].clear();
	ans=0;
	for(int i=1;i<n;++i) {
		int u,v;
		scanf("%lld%lld",&u,&v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	int tot=n,rt=0;
	auto get=[&](auto self,int p,int fa) -> void {
		cur[p]=0,siz[p]=1;
		for(int v:G[p]) {
			if(vis[v]||v==fa) continue;
			self(self,v,p);
			cur[p]=max(cur[p],siz[v]);
			siz[p]+=siz[v];
		}
		cur[p]=max(cur[p],tot-siz[p]);
		if(!rt||cur[p]<cur[rt]) rt=p;
	};
	get(get,1,0);
	dfs(rt);
	printf("%lld\n",(MOD+1)/2*ans%MOD);
}
signed main() {
	int T;
	scanf("%lld",&T);
	while(T--) solve();
	return 0;
}


H. The Faulty Tree

Problem Link

题目大意

给 \(n\) 个权值 \(w_1,w_2,\dots,w_n\)，A 和 B 分别构造一棵二叉树，以 \(1\sim n\) 为叶子并最小化 \(\sum_{i=1}^n w_i\times dep_i\)

其中 A 的二叉树上的每个节点都有 \(\ge 1\) 个儿子是叶子，现在 B 想要使他构造的二叉树的权值严格小于 A 构造的二叉树的权值，求出 A 至少要修改几个 \(w_i\) 的值，并给出方案（无 解输出 \(-1\)）

数据范围： \(n\le 10^6\)

思路分析

注意到 \(n\le 3\) 时两个人构造的树一定同构，因此直接输出

显然 A 会把叶子按权值从小到大，从深到浅排序

考虑在 A 构造的二叉树的基础上进行某种调整操作使得新树的权值更小

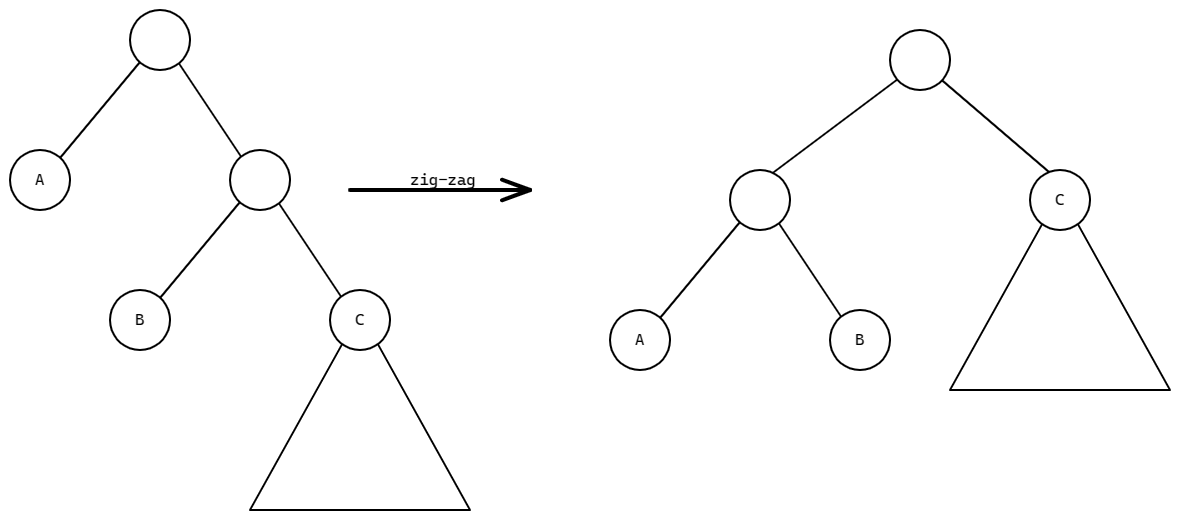
显然考虑对二叉树进行 zig-zag 操作，如下图：

p9pebxU.png

注意 \(A,B\) 是节点的权值，\(C\) 是子树的权值和，那么此时树的权值会加上 \(A-C\)

考虑回到序列上，假设 \(w_i\) 按升序排列，其前缀和记为 \(sum_i\)，那么序列 \(w\) 可以使 B 获胜当且仅当存在一个 \(3< i\le n\) 使得 \(w_i<sum_{i-2}\)，若这样的 \(i\) 已经存在，答案为 \(0\)，可以直接输出，而劣的做法一定是使得 \(w_i=w_{i-1}=w_{i-2}\)，此时 \(sum_{i-2}=sum_{i-3}+w_{i-2}=w_{i}+sum_{i-3}>w_i\)，因此答案至多为 \(2\)

考虑答案为 \(1\) 的情况，显然只有可能最小化 \(w_i\) 或最大化 \(sum_{i-2}\)，第一种情况尝试令 \(w_i\gets w_{i-1}\)，第二种情况尝试另 \(w_1\gets w_{i-1}\)，分别判断即可

容易证明不存在其他的策略

时间复杂度 \(\mathcal O(n\log n)\)

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+1;
int a[MAXN],sum[MAXN],p[MAXN],q[MAXN];
inline void solve() {
	int n;
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) scanf("%lld",&a[i]),p[i]=i;
	sort(p+1,p+n+1,[&](int x,int y){ return a[x]<a[y]; });
	for(int i=1;i<=n;++i) q[p[i]]=i;
	sort(a+1,a+n+1);
	if(n<=3) { puts("NO"); return ; }
	puts("YES");
	for(int i=1;i<=n;++i) sum[i]=sum[i-1]+a[i];
	auto print=[&]() { for(int i=1;i<=n;++i) printf("%lld ",a[q[i]]); puts(""); };
	for(int i=3;i<=n;++i) if(sum[i-2]>a[i]) { print(); return ; }
	for(int i=3;i<=n;++i) if(sum[i-2]>a[i-1]) { a[i]=a[i-1],print(); return ; }
	for(int i=3;i<=n;++i) if(sum[i-2]-a[1]+a[i-1]>a[i]) { a[1]=a[i-1],print(); return ; }
	a[n]=a[n-1]=a[n-2],print();
}
signed main() {
	int T;
	scanf("%lld",&T);
	while(T--) solve();
	return 0;
}