P7916 [CSP-S 2021] 交通规划 sol-最短路+环形dp-526互联

P7916 [CSP-S 2021] 交通规划 sol

Statement

传送门

Solution

好题。

发现 \(k\le 2\) 的分值非常多，于是我们考虑从 \(k=2\) 入手。

颜色相同就不用说了，直接染成同一种颜色就行了。

我们考虑其他情况，

就是颜色不相同的情况，我们一定是找了一条路径把这个图给切开了

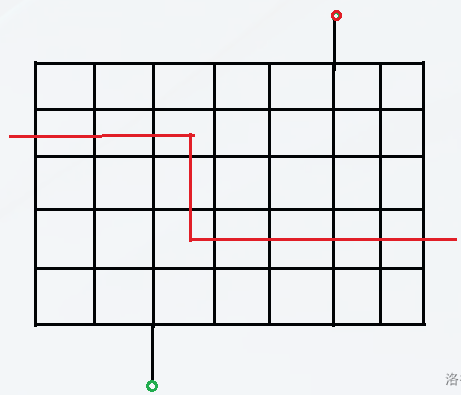
就像这个样子。

于是乎，在求的时候我们把格子变成点建图就可以了。

现在考虑对于其他情况，

可以尝试把平面图转换成最短路或最小割，

不难想到可以用 dinic 跑最大流，

就是你把黑色和白色附加点分别连向 \(S,T\)，

答案就是整个图的最小割，

也就是最大流。

这样可以做到 \(65\) 分，

如果用高级的网络流算法可以直接 AC。

现在考虑正解，

我们把附加点所分成的空白都看成点，

对于有意义（也就是两边颜色不同）的点，我们发现最终答案所构成的路劲一定是从这里面出发的。

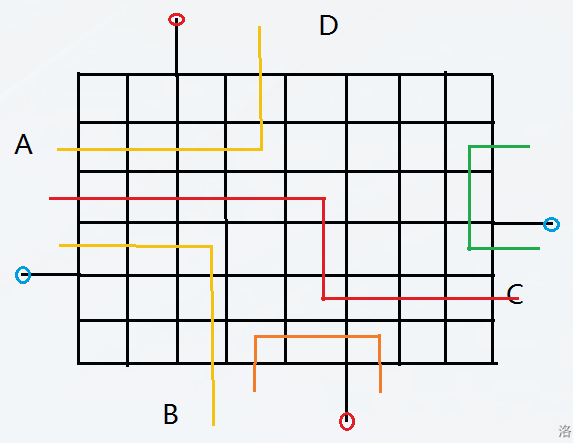
图中就有四个点 \(A,B,C,D\)

而 \(A,C\) 是本质相同的，因为他们都是红在蓝的顺时针方向。

我们在这些点之间跑最短路，

希望得到两两配对的最小的距离即为答案。

为什么是两两配对？

你可以感性理解一下，也可以去题解区理性证明，

其实画图模拟一下也可以知道。

而且我们需要链接两个 本质不同的点，

也就是说肯定不会去连 \(A,C\)，

很明显 \(A-C,B-D\) 一定没有 \(A-D,B-C\) 优，

并且我们也不会去连交叉的两条线，

这也很明显吧。

于是我们就有了基础的思路了。

我们先顺时针处理所有的附加点，遇到两个相邻的颜色相同算一个，于是就可以划分成两个点集 \(S,T\)，对于每一个 \(S\) ，我们都去跑一边 \(dij\)，从而求出了到每一个 \(T\) 的距离。

最后再进行一次环形 dp 算出所有情况的答案就可以了。

建图是有点烦的。

调了一天一夜~

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=505;
const ll inf=1e16;
int head[N*N],tot=1,n,m,T,s[N],t[N],c[N],id[N*N],cnts,cntt,cnt,k,idx=0;
bool vis[N*N];//都要是 N*N，tot是从1开始！！
ll dis[N*N],dp[N][N],g[N][N];
struct node{
  ll x;
  int p,t;
  bool operator <(const node& rhs) const{
    return p<rhs.p;
  }
}a[N];
struct edge{
  int v,nxt;
  ll w;
}e[(N*N)*8];

int read(){
  int x=0,f=1;char ch=getchar();
  while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
  while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

void add(int u,int v,ll w){
  e[++tot]=(edge){v,head[u],w};
  head[u]=tot;
  e[++tot]=(edge){u,head[v],w};
  head[v]=tot;
}

void dij(int st){
  for(int i=0;i<N*N;i++) dis[i]=inf;
  priority_queue<pair<ll,int> > q;
  dis[st]=0;
  q.push(make_pair(0,st));
  memset(vis,false,sizeof(vis));
  while(!q.empty()){
  	int u=q.top().second;q.pop();
  	if(vis[u]) continue;
  	vis[u]=true;
  	for(int i=head[u];i;i=e[i].nxt){
  	  int v=e[i].v;
	  if(dis[v]>dis[u]+e[i].w){
	  	dis[v]=dis[u]+e[i].w;
	  	q.push(make_pair(-dis[v],v));
	  }	
	}
  }
}

int cir(int x){return (x-1)%cnt+1;}
void sol(){
  k=read();
  cnt=0,cnts=0,cntt=0;
  for(int i=1;i<=idx;i++) e[i<<1].w=e[i<<1|1].w=0;
  for(int i=1;i<=k;i++){
  	a[i].x=1ll*read();a[i].p=read();a[i].t=read();
  	e[a[i].p<<1].w=e[a[i].p<<1|1].w=a[i].x;
  }
  sort(a+1,a+k+1);
  if(a[1].t==1&&a[k].t==0) s[++cnts]=a[1].p,c[++cnt]=a[1].p;
  if(a[1].t==0&&a[k].t==1) t[++cntt]=a[1].p,c[++cnt]=a[1].p;
  for(int i=2;i<=k;i++){
  	if(a[i].t==1&&a[i-1].t==0) s[++cnts]=a[i].p,c[++cnt]=a[i].p;
  	if(a[i].t==0&&a[i-1].t==1) t[++cntt]=a[i].p,c[++cnt]=a[i].p; 
  }
  if(cnts==0){puts("0");return;}
  sort(c+1,c+cnt+1);
  for(int i=1;i<=cnt;i++) id[c[i]]=i;
  memset(g,0x7f,sizeof(g));
  memset(dp,0x7f,sizeof(dp));
  for(int i=1;i<=cnts;i++){
  	dij(s[i]);
  	for(int j=1;j<=cntt;j++) g[id[s[i]]][id[t[j]]]=g[id[t[j]]][id[s[i]]]=dis[t[j]];
  }
    //环形dp
  for(int i=1;i<(cnt<<1);i++) dp[i][i+1]=g[cir(i)][cir(i+1)];
  for(int len=4;len<=cnt;len+=2)
    for(int i=1;i<=(cnt<<1)-len+1;i++){
      int j=i+len-1;
      dp[i][j]=dp[i+1][j-1]+g[cir(i)][cir(j)];
      for(int l=i+1;l<j;l+=2)
        dp[i][j]=min(dp[i][j],dp[i][l]+dp[l+1][j]);
	}
  ll ans=inf;
  for(int i=1;i<=cnt;i++) ans=min(ans,dp[i][i+cnt-1]);
  printf("%lld\n",ans);
}

int find(int i,int j){return (i-1)*m+j;}


void wrk(){
  n=read();m=read();T=read();
  idx=(n+m)*2;
  for(int i=1;i<idx;i++) add(i,i+1,0);
  add(idx,1,0);
  for(int i=1;i<n;i++)
    for(int j=1;j<=m;j++){
      ll x;
	  x=1ll*read();
      if(j==1) add(idx+find(i,j),idx-i+1,x);
      else if(j==m) add(idx+find(i,j-1),m+i+1,x);
      else add(idx+find(i,j-1),idx+find(i,j),x);
	}
  for(int i=1;i<=n;i++)
    for(int j=1;j<m;j++){
      ll x=1ll*read();
      if(i==1) add(idx+find(i,j),j+1,x);
      else if(i==n) add(idx+find(i-1,j),2*m+n-j+1,x);//注意是2*m+n!
      else add(idx+find(i-1,j),idx+find(i,j),x);
	}
	 
  while(T--) sol();
}

int main(){
  /*2023.9.23 H_W_Y P7916 [CSP-S 2021] 交通规划 最短路*/ 
  wrk();
  return 0;
}