2020-2021 ACM-ICPC Brazil Subregional Programming Contest-526互联

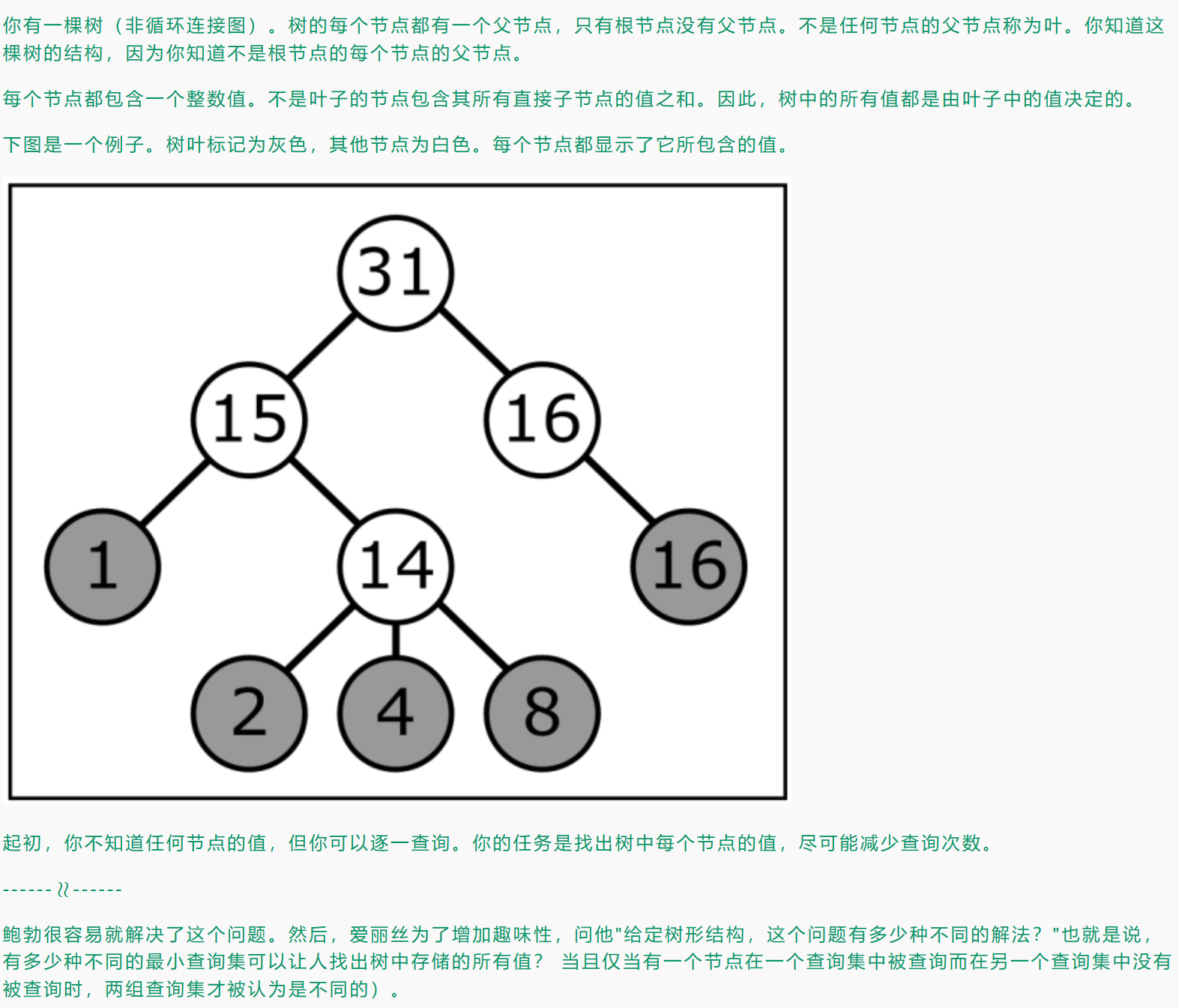
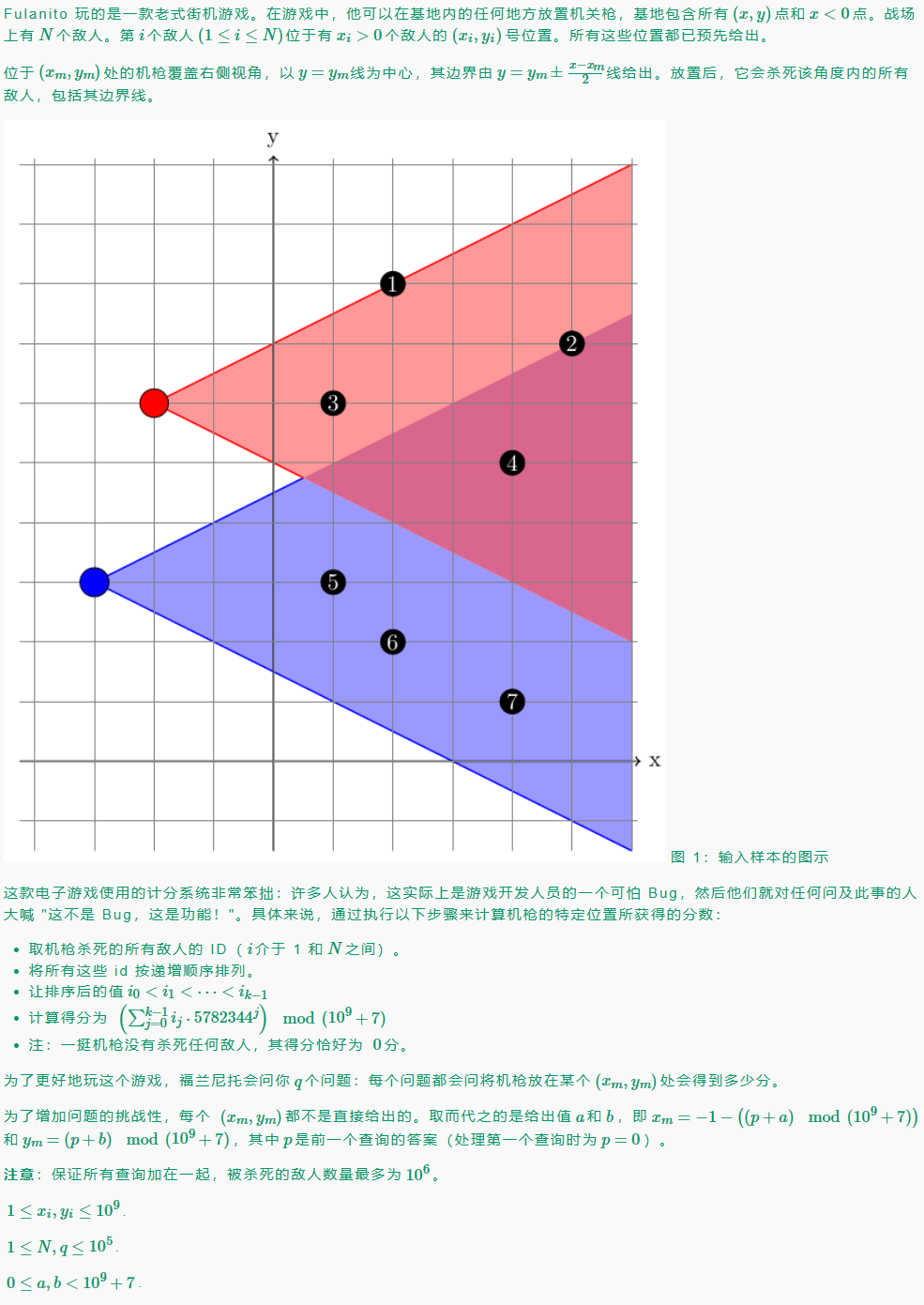
A. Sticker Album

你想要得到$n$张贴纸，每包礼物中等概率出现 $[A,B]$范围内数量的贴纸，求需要买多少包礼物才能至少获得$n$张贴纸的期望次数

$1 \leq n \leq 10^6,0\leq A,B\leq 10^6$

题解：期望DP

我们考虑从后往前进行$dp$

设计状态为$dp[i]$代表手上有$i$张贴纸时，至少获得$n$张贴纸的期望次数

显然初始状态：$dp[n]=dp[n + 1]...dp[∞] = 0$

容易得到状态转移方程：

\[ dp[i] = \sum_{j = i + a}^{j = i+b}(dp[j] + 1) \times \frac{1}{b - a + 1} , A \neq 0 \]

但是该题存在$A = 0$的情况，即自己转移到自己，这是一个经典的问题，我们不妨通过移项来解决该问题

\[ dp[i] =(dp[i]+1)\times \frac{1}{b - a + 1} + \sum_{j = i + a + 1}^{j = i+b}(dp[j] + 1) \times \frac{1}{b - a + 1}, A = 0 \\ dp[i] = \frac{b - a + 1}{b - a} + \sum_{j = i + a + 1}^{j = i+b}(dp[j] \times \frac{1}{b - a}), A = 0 \]

const int N = 2e6 + 10, M = 4e5 + 10;

int n, a, b;
double dp[N];
// dp[i] 代表手上有 i 张牌时，拿牌到 n 张牌的期望次数
// dp[n-∞] = 0

void solve()
{
    cin >> n >> a >> b;
    double sum = 0;
    if (a == 0)
    {
        for (int i = n - 1; i >= 0; --i)
        {
            sum += dp[i + a + 1];
            dp[i] += 1.0 / (b - a) * sum + 1.0 * (b - a + 1) / (b - a);
            sum -= dp[i + b];
        }
    }
    else
    {
        for (int i = n - 1; i >= 0; --i)
        {
            sum += dp[i + a];
            dp[i] += 1.0 / (b - a + 1) * sum + 1;
            sum -= dp[i + b];
        }
    }
    cout << fixed << setprecision(5) << dp[0] << endl;
}

E. Party Company

题解

考虑离线，由于对于一条链来说年龄单调，考虑将询问的左端点$L$挂在距离查询点最远的且年龄不超过$R$的节点上

因为单调，所以可以通过树上倍增来实现离线查询

然后在$dfs$的过程中回答询问，最朴素的想法是每次将节点的询问下放

实际上我们可以通过权值树状数组记录每个左端点的次数，对于某个节点$u$来说，它的答案为树状数组中所有比它小的左端点的个数

int n, q, w[N], fa[N][20], ans[N], c[N];
vector<int> g[N], vec[N];

int lowbit(int x) { return x & -x; }
void add(int x, int val)
{
    while (x < N)
    {
        c[x] += val;
        x += lowbit(x);
    }
}
int get_sum(int x)
{
    int res = 0;
    while (x > 0)
    {
        res += c[x];
        x -= lowbit(x);
    }
    return res;
}

void dfs1(int u, int par)
{
    if (u == 1)
        fa[u][0] = 1;
    else
        fa[u][0] = par;
    for (int i = 1; i <= 18; ++i)
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
    vector<int> tmp;
    for (auto v : g[u])
    {
        if (v == par)
            continue;
        tmp.push_back(v);
        dfs1(v, u);
    }
}

void dfs2(int u, int par)
{
    for (auto l : vec[u])
        add(l, 1);
    ans[u] = get_sum(w[u]);
    for (auto v : g[u])
    {
        if (v == par)
            continue;
        dfs2(v, u);
    }
    for (auto l : vec[u])
        add(l, -1);
}

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; ++i)
    {
        int u;
        cin >> w[i] >> u;
        if (i == 1)
            continue;
        g[u].push_back(i);
        g[i].push_back(u);
    }
    dfs1(1, 0);
    for (int i = 1; i <= q; ++i)
    {
        int u, l, r;
        cin >> u >> l >> r;
        for (int j = 18; j >= 0; --j)
        {
            if (w[fa[u][j]] <= r)
                u = fa[u][j];
        }
        vec[u].push_back(l);
    }
    dfs2(1, 0);
    for (int i = 1; i <= n; ++i)
        cout << ans[i] << "\n "[i < n];
}

H. SBC's Hangar

给定$n,k$，给定每个商品的重量$w[i]$，要求从$n$个商品中挑选$k$个商品，使得重量范围在$[L,R]$内的方案数

$1 \leq n,k \leq 50$

题解：数位$DP$

考虑到$n \leq 50$

考虑将所有商品排序后进行状态压缩，状态$i$代表$n$个商品选择的二进制状态

然后求出第一个大于等于$L$的二进制$l$，最大的小于等于$R$的二进制$r$

然后现在将问题转化为：在二进制$[l,r]$的范围内存在多少个二进制中的$1$的个数为$k$

考虑差分后数位$dp$即可

int n, k, a[N], L, R, dp[N][N][2][2], num[N];

int dfs(int pos, int sum, bool lead, bool limit)
{
    if (pos == 0)
        return (sum == k ? 1 : 0);
    if (dp[pos][sum][lead][limit] != -1)
        return dp[pos][sum][lead][limit];
    int res = 0;
    int up = (limit ? num[pos] : 1);
    for (int i = 0; i <= up; ++i)
    {
        if (i == 0 && lead)
            res += dfs(pos - 1, sum, true, limit && i == up);
        else if (i == 0)
            res += dfs(pos - 1, sum, false, limit && i == up);
        else
            res += dfs(pos - 1, sum + 1, false, limit && i == up);
    }
    return dp[pos][sum][lead][limit] = res;
}

int cal(int x)
{
    int len = 0;
    while (x)
    {
        num[++len] = x % 2;
        x /= 2;
    }
    memset(dp, -1, sizeof dp);
    return dfs(len, 0, true, true);
}

int check(int mid)
{
    int res = 0;
    for (int i = 0; i < n; ++i)
    {
        if (mid >> i & 1)
            res += a[i];
    }
    return res;
}

void solve()
{
    cin >> n >> k;
    for (int i = 0; i < n; ++i)
        cin >> a[i];
    sort(a, a + n);
    cin >> L >> R;
    int l = 0, r = (1ll << n) - 1;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (check(mid) >= L)
            r = mid - 1;
        else
            l = mid + 1;
    }
    int x = l;
    l = 0, r = (1ll << n) - 1;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (check(mid) <= R)
            l = mid + 1;
        else
            r = mid - 1;
    }
    int y = r;
    cout << cal(y) - cal(x - 1) << endl;
}

I. Interactivity

题解：树形$DP$

因为每颗子树中最多只能有一个叶子节点的值未知

所以考虑设计状态$dp[u][0/1]$代表以$u$为根的子树中，$0$代表所有叶子节点的值都已知，$1$代表还有$1$个叶子节点的值未知

考虑状态转移：

\[ dp[u][1] = \sum_{v_1 \in u的子树} dp[v_1][1] \times \prod_{v_2 \in u \and v_2\neq v_1} dp[v_2][0]\\ dp[u][0] = \prod dp[v][0] + dp[u][1] \]
对于$dp[u][0]$为什么可以从$dp[u][1]$转移过来，原因是如果有$1$个叶子节点的值位置，我可以通过查询$u$节点的值使得所有叶子节点的值已知，所以允许有$1$个叶子节点未知

$tips$：在$dp[u][1]$转移的过程中，会出现需要在一个序列中刨除一个数的问题，这里直接乘逆元会出错，对于这个经典的问题，我们考虑预处理前后缀即可

int n, dp[N][2];
vector<int> g[N];
// dp[u][0] : 以u为根的子树中叶已知所有叶子节点的值的方案数
// dp[u][1] : 以u为根的子树中仍存在1个叶子节点的值未知的方案数

void dfs(int u)
{
    if ((int)g[u].size() == 0)
    {
        dp[u][0] = dp[u][1] = 1;
        return;
    }
    for (auto v : g[u])
        dfs(v);
    vector<int> pre((int)g[u].size() + 10, 1), suf((int)g[u].size() + 10, 1);
    for (int i = 0; i < (int)g[u].size(); ++i)
    {
        int v = g[u][i];
        pre[i] = (i == 0 ? dp[v][0] : pre[i - 1] * dp[v][0] % mod);
    }
    for (int i = (int)g[u].size() - 1; i >= 0; --i)
    {
        int v = g[u][i];
        suf[i] = (i == (int)g[u].size() - 1 ? dp[v][0] : suf[i + 1] * dp[v][0] % mod);
    }
    for (int i = 0; i < (int)g[u].size(); ++i)
    {
        int v = g[u][i];
        if (i == 0)
            dp[u][1] = (dp[u][1] + dp[v][1] * suf[i + 1] % mod) % mod;
        else if (i == (int)g[u].size() - 1)
            dp[u][1] = (dp[u][1] + dp[v][1] * pre[i - 1] % mod) % mod;
        else
            dp[u][1] = (dp[u][1] + dp[v][1] * pre[i - 1] % mod * suf[i + 1] % mod) % mod;
    }
    dp[u][0] = (dp[u][0] + dp[u][1]) % mod;
    dp[u][0] = (dp[u][0] + suf[0]) % mod;
}

void solve()
{
    cin >> n;
    for (int i = 2, u; i <= n; ++i)
    {
        cin >> u;
        g[u].push_back(i);
    }
    dfs(1);
    cout << dp[1][0] << endl;
}

K. Between Us

给定$P$个人和$F$对关系，每对关系代表$u$和$v$是朋友，现在要求将所有的人最多分成两组，使得每个人在同一组中的朋友数量为奇数，询问是否有解

题解：高斯消元解异或方程组

假设分成的组的类别为$0， 1$

令$a[i]$为$i$的组别，即$a[i]=0/1$

如果$u$的朋友数量为奇数：

如果$u$在$0$中，那么他会有奇数个朋友也在$0$中，偶数个朋友会在$1$中

如果$u$在$1$中，那么他会有奇数个朋友也在$1$中，偶数个朋友会在$0$中

容易发现：对于$u$来说，其所有朋友分组的异或和等于$a[u]$，即$a[u] \oplus a[i] \oplus a[j]...a[k] = 0$

如果$u$的朋友数量为偶数：

如果$u$在$0$中，那么他会有奇数个朋友也在$0$中，奇数个朋友会在$1$中

如果$u$在$1$中，那么他会有奇数个朋友也在$1$中，奇数个朋友会在$0$中

容易发现：对于$u$来说，其所有朋友分组的异或和等于$1$，即$ a[i] \oplus a[j]...a[k] = 1$

列出$P$个异或方程组后高斯消元即可

int n, m, deg[N];
vector<int> g[N];

bitset<N> a[N];
int ans[N], Free[N], cnt; // 自由变量
int Gauss(int equ, int var)
{
    int row, col, MaxRow;
    col = 0;
    for (row = 0; row < equ && col < var; row++, col++)
    {
        MaxRow = row;
        for (int i = row + 1; i < equ; i++)
            if (abs(a[i][col]) > abs(a[MaxRow][col]))
                MaxRow = i;
        if (MaxRow != row)
            swap(a[row], a[MaxRow]);
        if (a[row][col] == 0)
        {
            row--;
            Free[++cnt] = col;
            continue;
        }
        for (int i = row + 1; i < equ; i++)
        {
            if (a[i][col])
                a[i] ^= a[row];
        }
    }
    for (int i = row; i < equ; i++)
        if (a[i][col])
            return -1; // 无解
    if (row < var)
        return var - row; // 无穷解
    for (int i = var - 1; i >= 0; i--)
    {
        ans[i] = a[i][var];
        for (int j = i + 1; j < var; j++)
            if (a[i][j])
                ans[i] ^= (a[i][j] && ans[j]);
    }
    return 0; // 唯一解
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= m; ++i)
    {
        int u, v;
        cin >> u >> v;
        --u, --v;
        g[u].push_back(v);
        g[v].push_back(u);
        ++deg[u], ++deg[v];
    }
    // n * (n + 1) 的增广矩阵
    for (int i = 0; i < n; ++i)
    {
        if (!deg[i])
        {
            cout << "N" << endl;
            return;
        }
        for (auto v : g[i])
            a[i].set(v);
        if (deg[i] & 1)
            a[i].set(i);
        else
            a[i].set(n);
    }
    int res = Gauss(n, n);
    if (res == -1)
        cout << "N" << endl;
    else
        cout << "Y" << endl;
}

M. Machine Gun

题解：二维偏序

考虑将所有敌人也通过两条射线投影到$y$轴上，那么会在$y$轴上形成$n$段区间$[l_i,r_i]$

那么对于每个询问，我们也将其投影在$y$轴上的区间$[L,R]$求出，然后就是求与该区间相交的所有区间的敌人编号

我们考虑什么情况是相交的：$r_i \geq L \and l_i \leq R$

显然是一个二位偏序问题，考虑将条件转化到二维平面上，横坐标为$l$，纵坐标为$r$

那么每个敌人的区间就是平面上一点，我所要求的就是一个向上无限延伸的矩形中的点的编号

因为我们要的是一个前缀中所有纵坐标大于等于$L$的点的编号，所以我们考虑树状数组，对每个位置$l$开一个$vector$，以二元组形式存放该位置上所有点的纵坐标和编号

那么对于一次查询来说，我只需要查询树状数组前$logR$个$vector$，然后在每个$vector$里面二分即可

因为保证所有被查询到的敌人不超过$1e6$，所以二分之后可以暴力将所有符合要求的敌人取出来

int n, q;
vector<int> vec;
array<int, 3> seg[N];
vector<array<int, 2>> c[N];

int lowbit(int x) { return x & -x; }
void add(int x, array<int, 2> val)
{
    while (x < N)
    {
        c[x].push_back(val);
        x += lowbit(x);
    }
}
vector<int> query(int x, int y)
{
    vector<int> res;
    while (x > 0)
    {
        int p = lower_bound(all(c[x]), array<int, 2>{y, 0}) - c[x].begin();
        for (int i = p; i < (int)c[x].size(); ++i)
        {
            if (c[x][i][0] >= y)
                res.push_back(c[x][i][1]);
        }
        x -= lowbit(x);
    }
    return res;
}

int find(int x) { return lower_bound(all(vec), x) - vec.begin() + 1; }

void solve()
{
    cin >> n >> q;
    for (int i = 1; i <= n; ++i)
    {
        int x, y;
        cin >> x >> y;
        int l = 2 * y - x, r = 2 * y + x;
        seg[i] = {r, l, i};
        vec.push_back(l);
    }
    sort(all(vec));
    vec.erase(unique(all(vec)), vec.end());
    sort(seg + 1, seg + n + 1);
    for (int i = 1; i <= n; ++i)
    {
        auto [r, l, id] = seg[i];
        l = find(l);
        add(l, array<int, 2>{r, id});
    }
    int ans = 0;
    while (q--)
    {
        int a, b;
        cin >> a >> b;
        int x = (-1 - ((ans + a) % mod)), y = (ans + b) % mod;
        int l = 2 * y + x, r = 2 * y - x;
        r = upper_bound(all(vec), r) - vec.begin();
        vector<int> vt = query(r, l);
        sort(all(vt));
        ans = 0;
        int pow = 1;
        for (int i = 0; i < (int)vt.size(); ++i)
        {
            ans = (ans + vt[i] * pow % mod) % mod;
            pow = pow * 5782344 % mod;
        }
        cout << ans << endl;
    }
}

N. Number Multiplication

题解

直接上科技：大数质因子分解

对每个数质因子分解后排序就好了

mt19937_64 rnd(time(0));
ll mx_fac;
// vector<int> fac;
map<int, int> mp;

ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }

ll qpow(ll a, ll b, ll p)
{ // 快速幂
    ll res = 1;
    while (b)
    {
        if (b & 1)
            res = (__int128)res * a % p;
        a = (__int128)a * a % p;
        b >>= 1;
    }
    return res;
}

bool Miller_Rabin(ll p)
{ // 判断素数
    if (p < 2)
        return 0;
    if (p == 2)
        return 1;
    if (p == 3)
        return 1;
    ll d = p - 1, r = 0;
    while (!(d & 1))
        ++r, d >>= 1; // 将d处理为奇数
    for (ll k = 0; k < 10; ++k)
    {
        ll a = rnd() % (p - 2) + 2;
        ll x = qpow(a, d, p);
        if (x == 1 || x == p - 1)
            continue;
        for (int i = 0; i < r - 1; ++i)
        {
            x = (__int128)x * x % p;
            if (x == p - 1)
                break;
        }
        if (x != p - 1)
            return 0;
    }
    return 1;
}

ll Pollard_Rho(ll x)
{
    ll s = 0, t = 0;
    ll c = (ll)rnd() % (x - 1) + 1;
    int step = 0, goal = 1;
    ll val = 1;
    for (goal = 1;; goal *= 2, s = t, val = 1)
    { // 倍增优化
        for (step = 1; step <= goal; ++step)
        {
            t = ((__int128)t * t + c) % x;
            val = (__int128)val * abs(t - s) % x;
            if ((step % 127) == 0)
            {
                ll d = gcd(val, x);
                if (d > 1)
                    return d;
            }
        }
        ll d = gcd(val, x);
        if (d > 1)
            return d;
    }
}

void divide_fac(ll x)
{
    if (x < 2)
        return;
    if (Miller_Rabin(x))
    {                            // 如果x为质数
        mx_fac = max(mx_fac, x); // 更新答案
        // fac.push_back(x);
        mp[x]++;
        return;
    }
    ll p = x;
    while (p >= x)
        p = Pollard_Rho(x);
    // 不用求质因子幂次时使用
    while ((x % p) == 0)
        x /= p;
    divide_fac(x), divide_fac(p); // 继续向下分解x和p
    // divide_fac(x / p), divide_fac(p);
}

int m, n, k;

void solve()
{
    cin >> m >> n >> k;
    for (int i = 1; i <= n; ++i)
    {
        int x;
        cin >> x;
        divide_fac(x);
    }
    for (auto [x, y] : mp)
        cout << x << " ";
    cout << endl;
}