20世纪70年代中期,在医学领域出现了一种神奇装置,名为“计算机辅助 X 射线断层成像仪”(简称CAT或CT),它能够在不损伤病人的情况下,提供人体从头到脚各部位的断层X射线图像。利用CT,医生可以轻而易举地观察到人体内部哪怕是极其微小的病变和病灶分布,能够及早采取正确的治疗措施,从而拯救无数患者的生命。
这个神奇装置是如何发明的呢?这就要从科马克接受的一次任务说起。
1955年,还是开普敦大学物理学讲师的科马克接到一项任务,要为南非一家医院的放射科监测肿瘤患者接受放射性同位素治疗的剂量。接受治疗的患者体内的同位素剂量及其分布会受到严格的控制。这是因为如果同位素剂量太小,将达不到理想的疗效;剂量太大,则会危害患者的健康。同时,同位素的浓度应在肿瘤组织内较高,在健康组织内尽可能低。
科马克想,是否可以通过体外测量同位素发出的射线,来确定其在体内的浓度分布,以帮助医师确定最佳治疗方法?他很快发现这其实是一个数学问题,如果这个问题解决了,很多问题都会迎刃而解。1963年,他发表了名为“函数的直线积分表示及其放射学应用”的开创性论文,通过自己的努力解决了这个数学问题。
这篇论文中包括研制CT的完整理论,而且也提到了三个实际应用:①确定二维区域内 X 射线吸收率的变化;②确定物质中正电子湮灭的非均匀分布;③确定恒定成分物质中的密度变化。
其实,早在1917年,奥地利数学家拉东就发表过一篇论文,文中提出一种变换方法,即对于一个定义在一定区域上的函数f,如何从该函数在以不同角度穿过该区域的直线上的积分值,来求得其分布解的变换方法。这个方法后来被称为“拉东变换”。科马克的工作其实就是重新发现“拉东变换”,并把它用于放射医学。
人体内部不同的组织具有不同的X射线吸收率。所以,如果能够知道人体内X射线吸收率的分布,就可以重建体内组织的图像了,这正是CT所要做的。从数学的角度来看,一根直线上的X射线平均吸收率就相当于在该直线上对于吸收率函数的积分值。因此,如果能根据函数在直线上的积分值来求出函数在各点的值,那么,就可以实现CT的功能了。这正是科马克在1963年的那篇论文中所完成的工作。
图像重建
由已知弦图求解CT图像可利用的算法:
直接矩阵求解法(Direct matrix inversion)
迭代法( iterative)
傅里叶重建法(Fourier reconstruction)
反投影法(Back-projection)
滤波反投影法(Filtered back projection)
1、Radon变换揭示了函数和投影之间的关系。
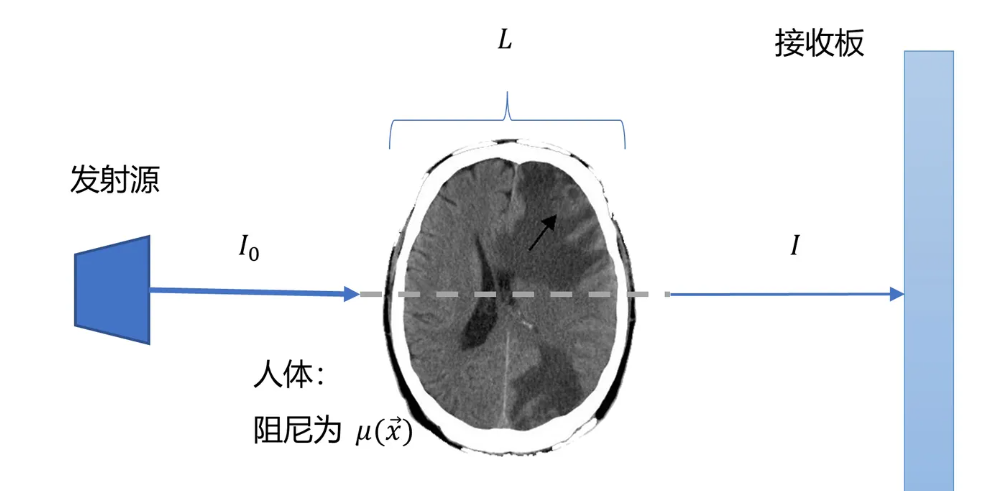
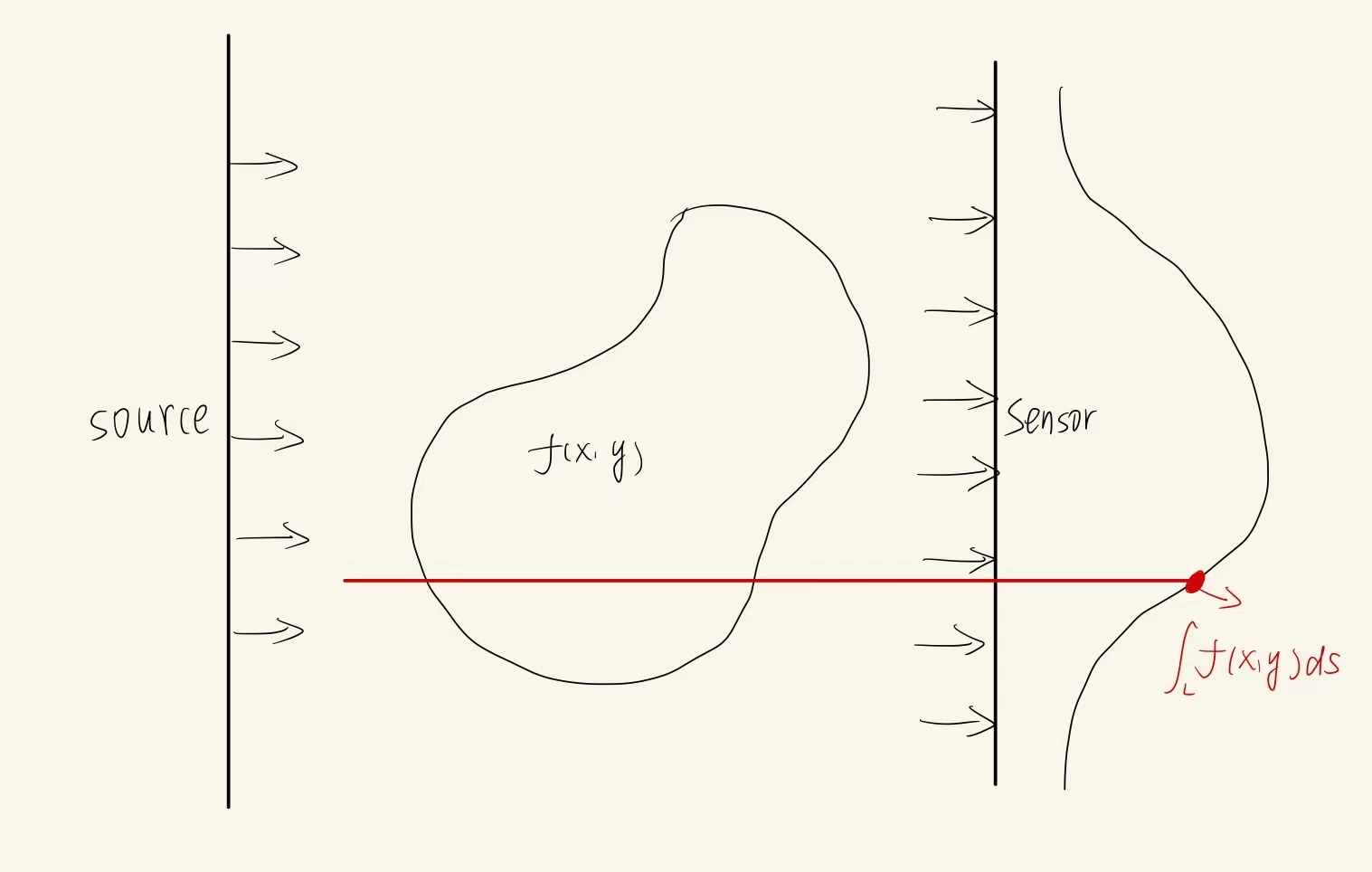
中间圆环是我们想要求的物体,左边是发射源能够发射一种射线,右边为感应器能够感应到射线的强弱,假设物体上每一点对射线的衰减程度为函数f(x,y) ,也可以称f(x,y)为密度函数,根据射线穿过物体的衰减程度可以得到物体在该方向上每一点的衰弱强度(intensity),如上图所示,相当于每个方向上都可以测量出该物体的“厚度”,我们的目的就是,根据不同方向上的物体的“厚度”求出物体上每一点的衰减程度.
如上图所示,转换为数学表达可以表示为一种线积分,直线 L 穿过 f(x,y),所对应的强度(intensity)就是函数f(x,y)在直线 L上的线积分
![]()
我们的目标是根据不同的线 L求出 f(x,y)的表达式,但定义里面包含f(x,y)的积分,想要求 f(x,y)的具体形式就要把该积分去掉,前人就想到了用傅立叶变换
前面的描述中说的是“在某一个方向上的每一个点的”衰减程度 → 某一个方向上的每一个点都可以表示为一条直线 L,那么我们需要用该方向来定义直线L,
先来看看 L的定义:
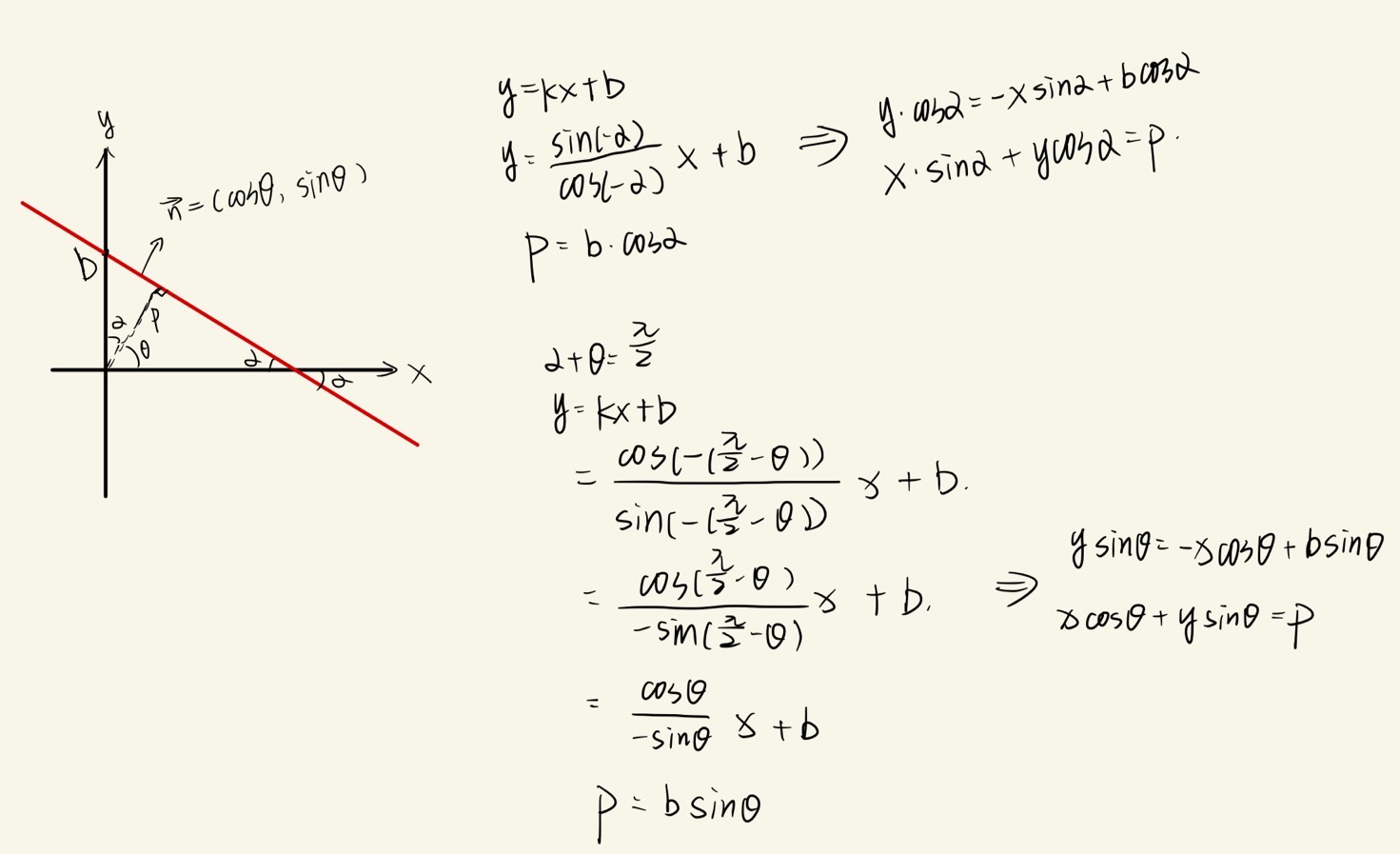
如上图所示,我们设直线方程为 y = kx + b ,直线 L远离原点的法线方向为n→=(cos(θ),sin(θ)),原点到直线的距离为 P ,则如上图公式所示,直线 L可表示为:
![]()
可以看到 θ 即为上图所说的方向, P 为该方向上的每一点放射源,则根据 (θ,P) 可以定义 拉东变换
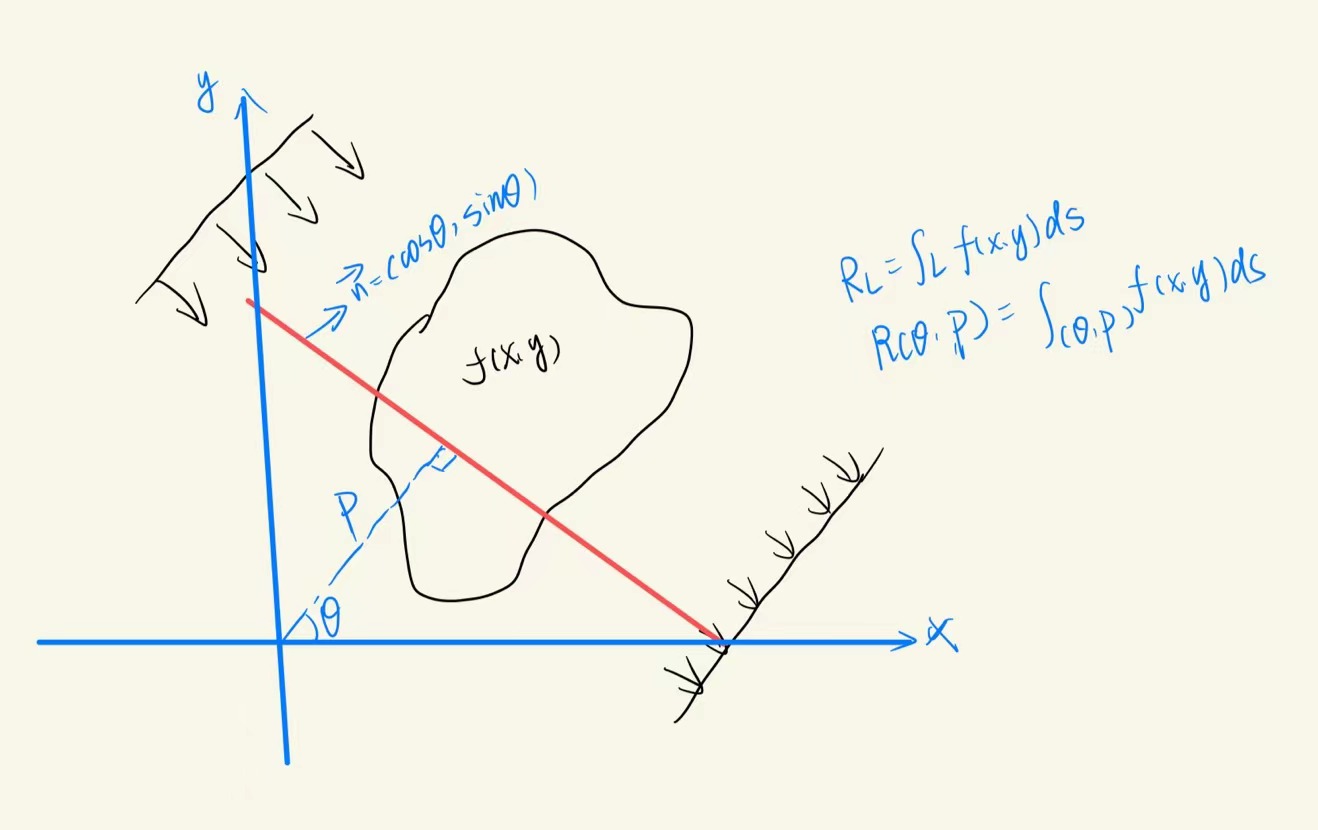

如果我们希望获得这个切片的全貌,我们可能需要从多个角度进行多次扫描,通过一维构建二维,在这里我们可以把对应的和制作成一个二维坐标系来绘图,叫做Sinogram:
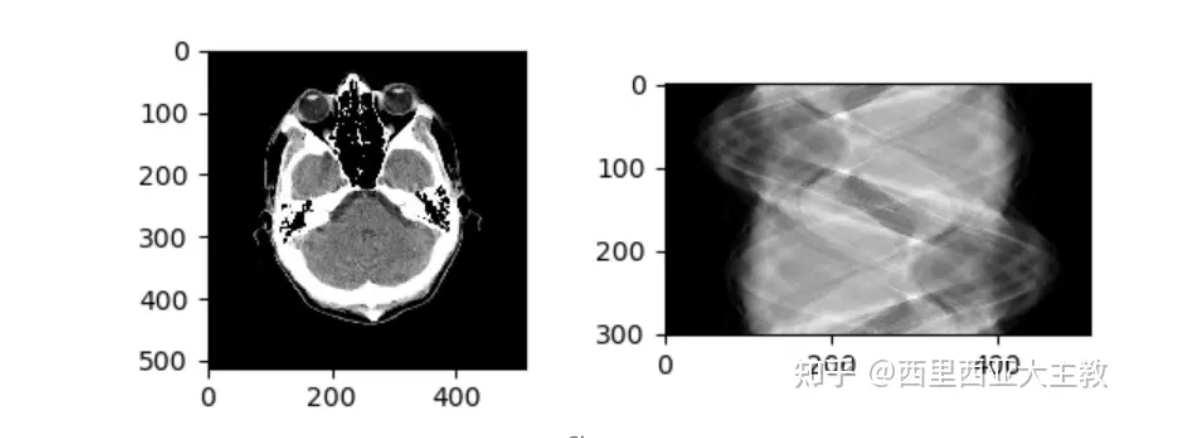
右图为Sinogram图,纵坐标为度数(360度等间距划分为300个间隔),横坐标自然是线到原点的距离。也就是说我们通过300次扫描(绕着切片一周)获得了Sinogram。从左边切片到有右边切片的过程我们叫做前向投影Forward Project。
2. 傅里叶切片定理 Fourier Slice Theorem
我们通过不同角度的投射得到了Sinogram。但是请注意,医疗实践中我们对于上图中的左图的信息是一无所知的,我们仅仅获得了右边的Sinogram(也就是说左边是空白)。那么我们如何通过Sinogram获得左边的图呢?
在此假设大家都明白傅里叶变换及其逆变换(如果不清楚的可以寻找相关资料,此为一信号处理方面十分重要的应用),即将时空域的信号转为频率域信号以及将频率域信号复转为时空域信号。傅里叶切片定理规定了如下几个要素:

我们知道我们希望求出f(x,y),那么这个f(x,y)根据某种投影(如拉东变换)再进行一维傅里叶变换,等价于这个f(x,y)的二维傅里叶变换的切片。
在这里解释切片:我们将原函数f(x,y)进行二维傅里叶变换后得到频率域坐标系(可以当作将原来的XY坐标系转移到某种UV坐标系),其切片为按照参数方程在该空间上选定的值,即(该θ角度可以理解成拉东变换的投影角度
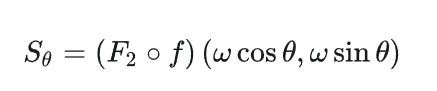

为了获取 f(x,y) ,基于我们已经知道的Sinogram(对应上图的 P θ) ,我们可以得到多角度的切片,根据这些切片重新组合较为完整的(实际上我们不可能也不需要填充整个二维傅里叶空间,只需要有限测量的几个投影即可)二维傅里叶空间,再将其进行逆变换获得到f(x,y)
傅立叶变换
在积分形式下得出函数的表达式第一想到的就是傅立叶变换,因为傅立叶变换及其性质里面就有把积分约掉的方法,这里用到的是傅立叶变换的卷积性质,为了能说清楚,自己也清楚一下
卷积:
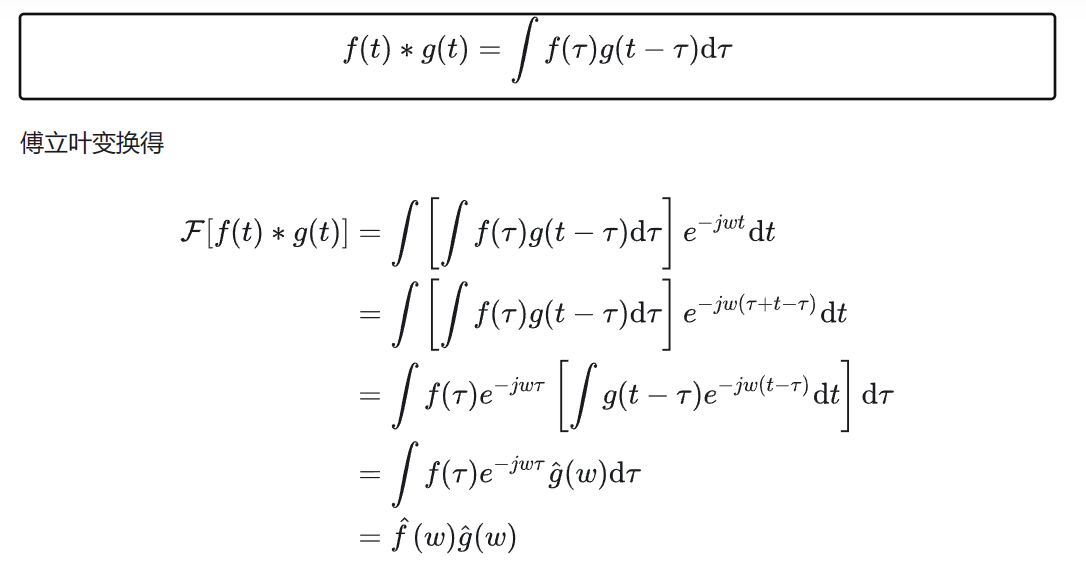


CT成像:在医学图像成像时,是通过x射线穿过人体来实现的,射线穿过人体后会衰减,然后被仪器测量到,也就是说我们已经知道了拉东变换的结果,需要通过这个结果还原出射线穿过的人体剖面,即拉东逆变换。
其余还有反投影,滤波反投影方法等,反投影算法出现星状伪影的现象,用滤波反投影运用了卷积,弥补了反投影算法的缺陷............