一道笛卡尔树的经典题。
我们用样例解释:
5
2 3 1 2 4
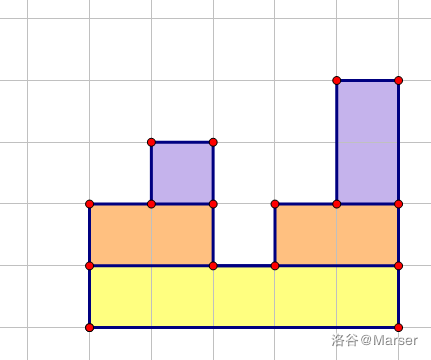
我们可以建一棵笛卡尔树使\(h_i\)满足小根堆性质,\(i\)满足二叉树性质
这棵笛卡尔树使这个直方图分成若5个矩阵,笛卡尔树上的每一节点代表一个矩阵,矩阵\(x\)的长就是以\(x\)点为根的子树大小\(siz_x\),高度就是\(h_x-h_{fa_x}\),这道题就转化成了树形DP问题了。
令\(f_{i,j}\)表示以\(i\)为根的子树放了\(j\)个相同的数的合法方案数
令\(g_{i,j}\)表示只在\(i\)的儿子所在的子树中放\(j\)个相同的数的合法方案数
则有:
解释:笛卡尔树的每个节点最多只有两个儿子,所以用算\(g_{i,j}\)时左儿子乘右儿子就可以了。
\(g_{i,p}\)就是从节点\(i\)的儿子中放\(p\)个相同的数的方案数
\(C_{siz_i-p}^{j-p}\)因为从节点\(i\)的儿子中选了\(p\)个相同的数,而每个相同的数不能同列,所以这\(p\)个数必然使用了\(p\)行,所以要从剩下\(siz_i-p\)行中选出\(j-p\)行用来放相同的数
\(C_{h_i-h_{fa_i}}^{j-p}\)因为不管选哪一列都不会跟它的儿子在同一行,所以可以从\({h_i-h_{fa_i}}\)选\({j-p}\)列放相同的数(不必管是否会在同一列,那是\(C_{siz_i-p}^{j-p}\)考虑的事)
\(A_{j-p}^{j-p}\)因为选出了\(j-p\)行\(j-p\)列,我们在选出的第\(1\)行可以选择将数放在\(j-p\)列中的任意一列,而选出的第二行可以选择将数放在\(j-p-1\)列中的任意一列,以此类推,有\(A_{j-p}^{j-p}\)中方案
计算答案:
输出\(f_{rt,k}\),其中\(rt\)时树根,\(k\)是要放的相同的数的个数
时间复杂度:
\(O(nk^2)\)