首先我们先考虑只询问 \(1\) 节点的情况。
那么这时候我们是一个以 \(1\) 节点为根的有根树。
这时候我们要选择 \(k\) 条路径,使得所有点到这 \(k\) 条路径其中之一的最短距离的和最小。
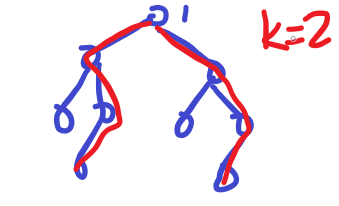
对于 \(k=2\) 我们就可以这样选。
但是直接选路径实际上不太好考虑,我们可以拆贡献,转化一下,变成每条边的贡献。
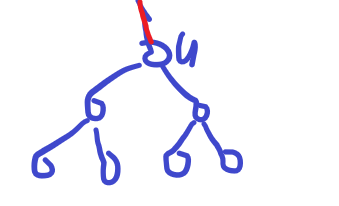
我们考虑 \(u\) 与他父亲相连的边的贡献是多少,如果选了他父亲这条边,那么贡献就是 \(0\) ,如果没选的话,那么贡献就是 \(u\) 子树中的 \(w\) 的和。(不存在子树里有边选了,而 \(u\) 与他父亲的边没选的情况)
这时候我们的问题就转化成了,从图中选 \(k\) 条可重路径出来,使得至少被一条路径包含的边的权值和最大,这样我们用总数减去这个最大就可以得到最小的答案。
这时候如何处理呢。
考虑贪心,假如我们只能选一条路径,我们肯定是选最大的,假如是红色这条。
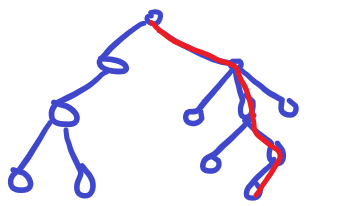
而加入我们能选两条路径,我们第一条仍然是选择最大的,因为如果存在一种方案不选这个最大的路径,那么一定可以将一条路径调整成最大的这条,不劣。而如果存在一条路径选最大,另一条选了其他的,那么我们第一条选最大,也一定是不劣的。
所以我们最大的一定要选。
所以这样我们就可以把原树剖成若干条链,每条链的权值和就是这条路径所能获得的权值和。
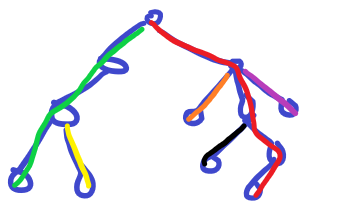
具体长成这样。
所以我们就要维护前 \(k\) 大的链的权值和,然后加起来就是我们的答案了。
我们可以维护两个 \(multiset\) ,其中一个存的是前 \(k\) 大的,另一个存的是剩下的。
那么我们处理一次的时间复杂度是 \(O(n\log n)\)
如果对于所有点都这样处理的话,那么实际上总时间复杂度是 \(O(n^2\log n)\)
考虑进一步优化。
我们考虑换根 \(dp\) 。
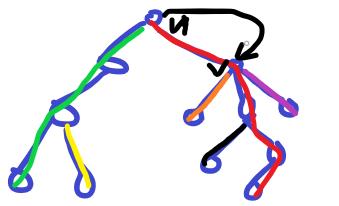
假如从 \(u\) 走到 \(v\)
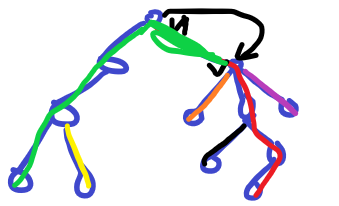
那么实际上就只有 \(O(1)\) 条边是被改变的,一个是原本包含 \(u\sim v\) 这条边的链的权值减少了,一个是从 \(u\) 进来的最长的边增加了 \(u\sim v\) 这条边的权值(不过这条边的权值和原本是不一样的,再算一下就好了)
所以我们只用修改两条边的权值就行了。
然后用我们上面所说的 \(multiset\) 维护前 \(k\) 大即可。
时间复杂度 \(O(n\log n)\)
`#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int MAXN=2e5+10;
int n,k;
int a[MAXN];
vector
void add(int f,int t) {
e[f].push_back(t);
}
LL sz[MAXN],co[MAXN],Fa[MAXN],maxn[MAXN],cost[MAXN],fr[MAXN],total;
//co 链的最大值
//Fa 是否是链的顶端
//maxn 最大链的方向
//cost 其他点到他的距离
//fr 可以减去的最大距离
LL ans[MAXN];
void dfs(int u,int fa) {
sz[u]=a[u];
for(auto t:e[u]) {
if(t==fa) continue;
dfs(t,u);
sz[u]+=sz[t];
if(co[t]>co[maxn[u]]) maxn[u]=t;
cost[u]+=cost[t]+sz[t];
}
Fa[maxn[u]]=u;
co[u]=(u!=1?sz[u]:0)+co[maxn[u]];
}
multiset
LL sum=0;
void update(LL x) {
if(s1.size()<k) {
s1.insert(x);
sum+=x;
}
else s2.insert(x);
LL l1=s1.size(),l2=s2.size();
while(l1&&l2) {
auto it=s1.begin(),itt=s2.end();
--itt;
LL x=it,y=itt;
if(x<y) {
s1.erase(it);
s2.erase(itt);
sum+=y-x;
s1.insert(y);
s2.insert(x);
}
else break;
}
}
LL res;
void dele(LL x) {
if(s1.count(x)) {
auto it=s1.lower_bound(x);
s1.erase(it);
sum-=x;
while(s1.size()&&s2.size()) {
int l1=s1.size(),l2=s2.size();
if(l1<k) {
if(!l2) return ;
auto it=s2.end();
--it;
LL x=*it;
sum+=x;
s1.insert(x);
s2.erase(it);
}
else break;
}
}
else {
auto it=s2.lower_bound(x);
s2.erase(it);
}
}
LL mx,ind[MAXN],tot;
bool vis[MAXN];
void zx(LL x,LL y) {
dele(x);
update(y);
}
void dfs1(int u,int fa,LL FAFA,bool sf_l) {
fr[u]=sum;
int mx=0;
if(sf_l) {
for(auto t:e[u]) {
if(tfa) continue;
if(co[t]>co[mx]) mx=t;
}
FAFA=co[mx];
}
for(auto t:e[u]) {
if(tfa||vis[t]) continue;
cost[t]=cost[u]+(total-sz[t])-sz[t];
zx(co[t],co[t]-sz[t]);
LL ls=FAFA,lss;
lss=ls+(total-sz[t]);
zx(ls,lss);
dfs1(t,u,lss,0);
zx(co[t]-sz[t],co[t]);
zx(lss,ls);
res=0;
}
}
int main () {
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]);
total+=a[i];
}
for(int i=1;i<n;++i) {
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dfs(1,0);
co[1]=0;
for(int i=1;i<=n;++i) {
if(!Fa[i]) {
update(co[i]);
}
}
int x=1;
while(x) {
vis[x]=1;
ind[++tot]=x;
x=maxn[x];
}
update(0);
for(int i=1;i<=tot;++i) { res=ind[i];
zx(co[ind[i]],co[maxn[ind[i]]]);
dfs1(ind[i],0,0,1);
if(i<tot) {
int j=ind[i];
co[j]=0;
for(auto t:e[j]) {
if(t==ind[i+1]) continue;
co[j]=max(co[j],co[t]);
}
zx(co[j],co[j]+total-sz[ind[i+1]]);
co[j]=co[j]+total-sz[ind[i+1]];
}
cost[ind[i+1]]=cost[ind[i]]+(total-sz[ind[i+1]])-sz[ind[i+1]];
}
for(int i=1;i<=n;++i) printf("%lld\n",cost[i]-fr[i]);
return 0;
}`