[CTS2023] 另一个欧拉数问题解析-526互联

题目大意

对于正整数 \(\alpha\), 考虑下述长为 \(\alpha n\) 的序列 \(a\):

对于每个 \(k=1,\dots, n\), 序列 \(a\) 中出现了恰好 \(\alpha\) 个 \(k\).
对于 \(i < j\) 满足 \(a_i = a_j\), 那么对任意 \(i < k < j\), 有 \(a_k \geq a_i\).

我们称满足上述要求的序列是一个 \(n\) 阶的 \(\alpha\)-排列. 现在输入一个 \(n_0\) 阶 \(\alpha\)-排列 \(P\). 又给定 \(n, m\), 请你计算有多少 \(n\) 阶 \(\alpha\)-排列包含子序列 \(P\), 并且满足:

总共有 \(m\) 个下标 \(i\) 满足 \(a_i > a_{i+1}\).

只需计算出这样的序列总数对 \(998244353\) 取模的结果.

解法概要

不难注意到, 对于输入的序列 \(P\), 我们只关心它具有多少个下标满足 \(a_i > a_{i+1}\), 记为 \(m_0\).

考虑将所有值为 \(n\) 的数插到序列中, 根据要求, 它们此时必须是相邻的, 分类讨论所插入的位置是否对 \(m\) 有所贡献, 得到递推式

\[F_{n,m} = (\alpha(n-1) + 1 - m)F_{n-1,m-1} + (m+1)F_{n-1,m}. \]

初始条件是 \(F_{n_0,m_0}=1\).

通过某些方法研究 \(\alpha=1\) 的情况, 发现答案的一行可以表为

\[(1-x)^{n+1}\left(\sum_{k=0}^\infty (k+1)^{n-n_0} \binom{k-m_0 + n_0}{n_0} x^k\right). \]

这个形式看起来具有美丽的结构. 考虑我们的递推系统, 在 \(\alpha=1\) 的情况下是

\[E_{n,m} = (n-m)E_{n-1,m-1} + (m+1)E_{n-1,m}. \]

如果我们填下了第 \(n_0\) 行, 如何计算出递推得到的 \(n\) 行? 根据前述答案的线性性, 我们应该这么做:

\[{\color{red}\frac{E_{n+1}}{(1-x)^{n+1}}}=\left(\frac{d}{dx}x\right)^{n-n_0}{\color{red}\left(\frac{E_{n_0}(x)}{(1-x)^{n_0+1}}\right)}. \]

类似地, 我们会发现对于一般的 \(\alpha\), 令 \(G_n(x) = xF_n(x) / (1-x)^{\alpha n + 1}\) 时, 我们将第 \(n\) 行到第 \(n+1\) 行的递推进行了变换

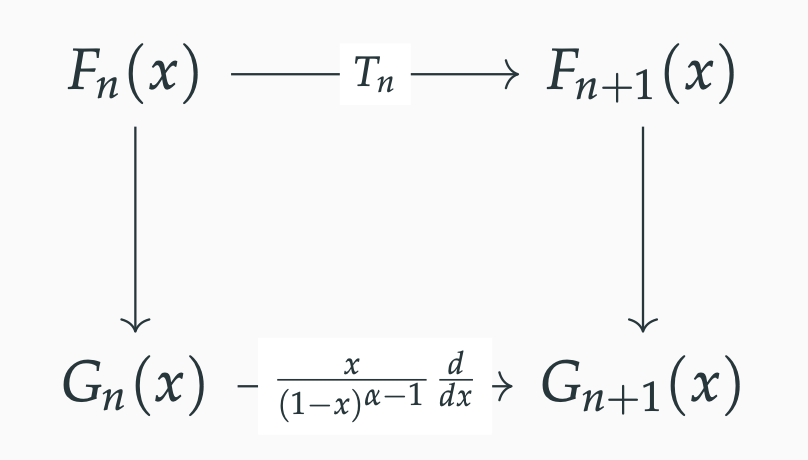
注意下面的变换是和 \(\boldsymbol{n}\) 无关的.

比较

\[E_{n} = xE_{n-1}', \quad G_n = \frac{x}{(1-x)^{\alpha-1}}G'_{n-1}. \]

我们不喜欢后者, 但喜欢前者, 因为前者的变换做 \(k\) 次, 只需要个快速幂.

所以要让后者变成前者. 直接设 \(G_n = H_n \circ y(x)\), 我们希望 \(H_n(y) = yH_{n-1}'(y)\). 方程会回应我们的希望, \(y\) 只需要是

\[\frac{x}{(1-x)^{\alpha-1}}y' \]

的解.

\(y\) 的复合逆是好求的 (但常数上是大头), 因此我们可以容易地算出 \(H_{n_0}(y)\) 的关于 \(y\) 的系数. 然后算出 \(H_{n}(y)\), 然后 Lagrange 反演公式计算 \(F_n(x)\) 的某一项的系数. 时间复杂度 \(O(n\log n)\).

若干注记

Remark 1 我们已经初步掌握了含参递推系统的一些基本的 trick, 第一步是消去参数, 第二步是把固定的线性变换做对角化.

See Also 1 比如这些 trick 立刻可以用来给嘘月做一个计算的解法...

多余的话

本来这题被毙了啊, 但是由于某些原因另一位清华大学李姓长发毒瘤出题人被 ban 了, 所以要换一个题上...
这可能是我最不讲武德的一次出题... 大家笑一笑就好...

526互联

[CTS2023] 另一个欧拉数问题 解析

题目大意

解法概要

若干注记

多余的话

[CTS2023] 另一个欧拉数问题解析