图论杂项
目录
拓朴排序
遍历(常应用于缩点后)
首先,对于遍历拓朴排序,很简单,bfs每次进入入度为0的点进来做,然后所有他连的点入度-1(相当于删除这个点)。
递归/dp等的遍历(剪枝)
这一点是我要详细介绍的。
首先,肯定可以知道的是,这个图肯定是可以dfs的。
具体的做法和树上dfs差不多,而且还不用考虑返祖(有向无环,我从根开始只能不断往下,不能往回)。
但是他和树形结构不同,因为他可能存在儿子节点汇聚的情况,从而使时间复杂度恶化。
但是,很有可能超时,考虑这样一个图
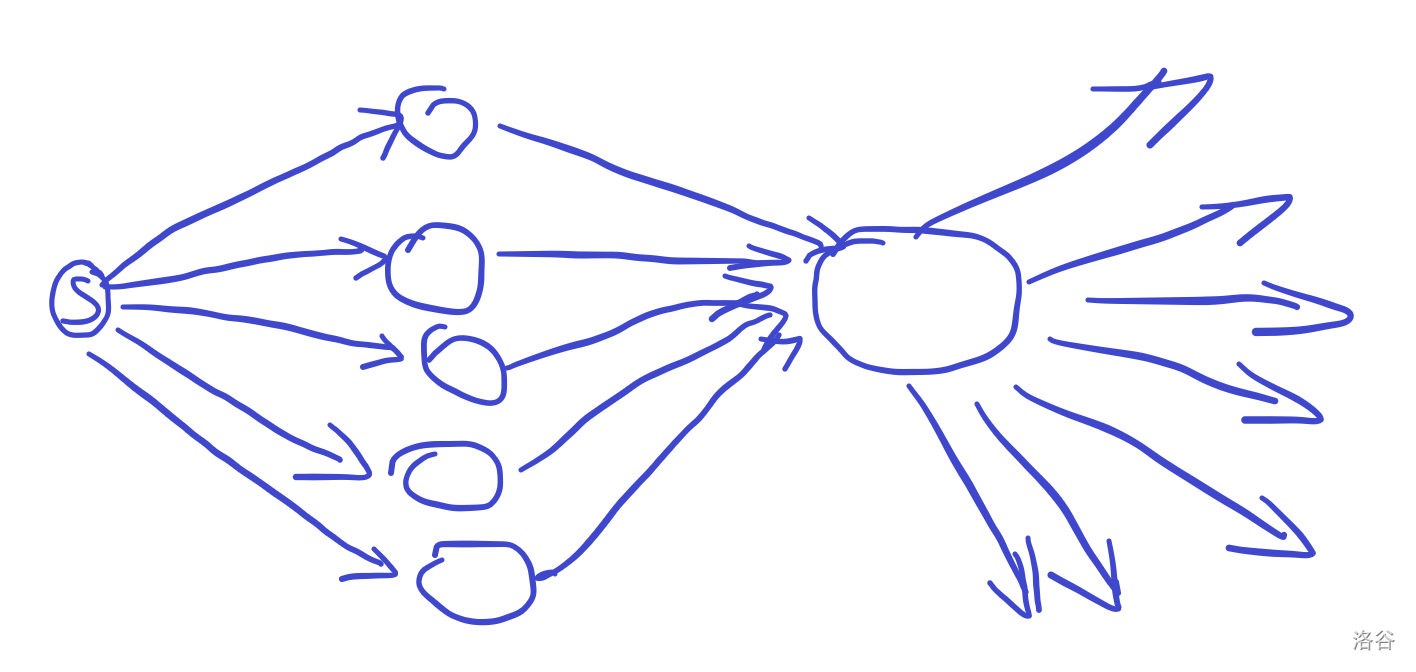
这样跑dfs的话会重复跑一个点。
所以说,类似记忆化搜索,如果统计完一个点,第二次遇到时立即return。
例题:[NOIP2009 提高组] 最优贸易
https://www.luogu.com.cn/problem/P1073
注:这是我自己想出来的优化做法,做这道题你还是要先知道点双边双
然后呢,这道题还有两次dfs,原因是你必须走到n点。
至于记忆化搜索看什么,看你想统计什么即可
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
/*
[NOIP2009 提高组] 最优贸易
因为走边不需要花费,所以一个环内随便走。但是走过单向边又不在一个分块内就不能回来了
缩点,形成DAG
然后就是买卖问题了
但是有个很jb烦的问题,他必须要走完所有的点
https://www.luogu.com.cn/discuss/364763
没筛除只有20分
我可以反着来一次找?
*/
const int N=100005;
int buy[N];
vector<int>mp[N];
vector<int>bcc[N];
vector<int>bccmp[N];
vector<int>revbc[N];
int dfn[N],low[N],s[N],col[N];
int inbc[N],buybc[N],sellbc[N];//缩点后入度,缩点后该点购入最小值和售出最大值
int top,cnt,t;
bool vis[N],should[N];
int maxsell[N];
void tarjan(int x,int fa){
t++;
top++;
s[top]=x;
dfn[x]=low[x]=t;
vis[x]=1;
for(int i=0;i<mp[x].size();i++){
int to=mp[x][i];
if(!dfn[to]){
tarjan(to,x);
low[x]=min(low[x],low[to]);
}
else if(vis[to]){
low[x]=min(low[x],dfn[to]);
}
}
if(low[x]==dfn[x]){
cnt++;
while(s[top+1]!=x){
bcc[cnt].push_back(s[top]);
buybc[cnt]=0x3f3f3f3f;//初始化
vis[s[top]]=0;
col[s[top]]=cnt;
top--;
}
}
}
int ans=0;
int n,m;
void predfs(int x){
if(should[x]==0){
should[x]=1;
}
else{
return;//剪枝,说明后面的能到的肯定已经全部ok了
}
for(int i=0;i<revbc[x].size();i++){
int to=revbc[x][i];
predfs(to);
}
}
int dfs(int x){//返回最大卖出值 ,关键在于怎么找必须要到达n的路径,其他的要筛除
if(should[x]==0){//不在路径上
return -1;//我让你售出都亏,你就不会选走这里了吧
}
if(maxsell[x]!=-1){
return maxsell[x];
}
int ret=sellbc[x];
ans=max(sellbc[x]-buybc[x],ans);
for(int i=0;i<bccmp[x].size();i++){
int to=bccmp[x][i];
if(should[to]==0){
continue;
}
int cost=buybc[x];
ans=max(ans,dfs(to)-cost);
ret=max(ret,dfs(to));
}
if(bccmp[x].size()==0){
return maxsell[x]=sellbc[x];
}
return maxsell[x]=ret;
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++){
maxsell[i]=-1;
scanf("%lld",&buy[i]);
}
for(int i=1;i<=m;i++){
int a,b,op;
scanf("%lld%lld%lld",&a,&b,&op);
if(op==1){
mp[a].push_back(b);
}
else{
mp[a].push_back(b);
mp[b].push_back(a);
}
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
top=0;
tarjan(i,i);
}
}
for(int x=1;x<=n;x++){
for(int i=0;i<mp[x].size();i++){//实际意义是便利所有的边
int bc=col[x];
int to=mp[x][i];
int tobc=col[to];
buybc[bc]=min(buybc[bc],buy[x]);
buybc[tobc]=min(buybc[tobc],buy[to]);
sellbc[bc]=max(sellbc[bc],buy[x]);
sellbc[tobc]=max(sellbc[tobc],buy[to]);
if(bc==tobc){
continue;
}
else{
inbc[tobc]++;
bccmp[bc].push_back(tobc);
revbc[tobc].push_back(bc);
}
}
}
int st=col[1];
int ed=col[n];
predfs(ed);//从n往回走确定正确的点对
dfs(st);
printf("%lld",ans);
}
应用问题(怎么翻译出拓朴排序)
例题:
CodeForces 730E
「BZOJ3355 Usaco2004 Jan」有序奶牛
主要是找到有向和无环两个条件,然后抽象意义建图,然后遍历即可。
甚至第一道题找到性质可以不用建图
欧拉回路
定义:
如果图G中的一个路径包括每个边恰好一次,则该路径称为欧拉路径(Euler path)。
如果一个回路是欧拉路径,则称为欧拉回路(Euler circuit)
例题:[省选联考 2020 B 卷] 丁香之路
https://www.luogu.com.cn/problem/P6628
主要在于题目的分析
仔细看题目:每一条路都开了花,换句话说,要走完这个图
然后刚开始题意理解错了,他是两两点间都可以走,不过m条边必须要走
然后思路就比较清晰了:
首先每个终点跑一个欧拉路径感觉不太行,超市肯定的
那么,我要是起点和终点连上一条边,就可以形成一个欧拉回路。
那么,为了让这个欧拉回路最短,我肯定连尽量近的点。心地把度数为奇数的点和它的下一个点相连;
建完边后可能不连通
那么我们把已有的连通块用并查集缩点,然后求最小生成树,
让图连通的最小代价就是最小生成树大小的两倍。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
/*
仔细看题目:每一条路都开了花,换句话说,要走完这个图
然后刚开始题意理解错了,他是两两点间都可以走,不过m条边必须要走
然后思路就比较清晰了:
首先每个终点跑一个欧拉路径感觉不太行,超市肯定的
那么,我要是起点和终点连上一条边,就可以形成一个欧拉回路。
那么,为了让这个欧拉回路最短,我肯定连尽量近的点。心地把度数为奇数的点和它的下一个点相连;
建完边后可能不连通
那么我们把已有的连通块用并查集缩点,然后求最小生成树,
让图连通的最小代价就是最小生成树大小的两倍。
甚至不用最小生成树45分......
*/
const int N=2505;
struct edge{
int x,y,w;
}e[N];
int n,m,s,cnt,ans,k,B[N*N];
int deg[N],fa[N],pf[N],b[N<<1];
int find(int x){
if(fa[x]==x){
return x;
}
else return fa[x]=find(fa[x]);
}
void he(int x,int y){
x=find(x);y=find(y);
if(x==y){
return;
}
fa[x]=y;
return;
}
bool cmp(edge x,edge y){
return x.w < y.w;
}
void krus(){
for(int i=1;i<=k-1;i++){
int x=find(e[i].x),y=find(e[i].y);
if(x==y)continue;
fa[x]=y;ans+=e[i].w*2;
}
}
signed main(){
scanf("%lld%lld%lld",&n,&m,&s);
int sum=0;
for(int i=1;i<=n;i++){
fa[i]=i;
}
for(int i=1,x,y;i<=m;i++){
scanf("%lld%lld",&x,&y);
he(x,y);
deg[x]++;
deg[y]++;
B[++cnt]=x;B[++cnt]=y;
sum+=abs(x-y);//最少话费先加了再说
}
B[++cnt]=s;
sort(B+1,B+1+cnt);
cnt=unique(B+1,B+1+cnt)-B-1;
for(int i=1;i<=n;i++){
pf[i]=find(i);
}
deg[s]++;
m=0;
for(int ed=1;ed<=n;ed++){
deg[ed]++;
ans=sum;
int last=0;
for(int i=1;i<=cnt;i++){
b[i]=B[i];
}
k=cnt;
b[++k]=ed;
sort(b+1,b+1+k);
k=unique(b+1,b+1+k)-b-1;
for(int i=1;i<=n;i++){
fa[i]=pf[i];
}
for(int i=1;i<=n;i++){
if(deg[i]%2==1){
if(last){
for(int j=last;j<i;j++){
he(i,j);
}
ans+=i-last;//欧拉路连了一个边
last=0;//保证为偶数deg就跑
}
else last=i;
}
}
for(int i=1;i<=k-1;i++){
e[i]=(edge){b[i],b[i+1],b[i+1]-b[i]};
}
sort(e+1,e+k-1+1,cmp);
krus();
printf("%lld ",ans);
deg[ed]--;//注意,这里要--保证不对下一次出现错误
}
return 0;
}
树上hash
树上哈希,即给树一个映射值,常用于判断两个数是不是同构的
同构含义:
若将某个点作为根,从根开始遍历,则其它的点都有一个前驱,这个树就成为有根树。
对于两个树T1和T2,如果能够把树T1的所有点重新标号,使得树T1和树T2完全相
同,那么这两个树是同构的。
树上hash做法
相当于给每个树的结点进行了转化,假设这个转化为h(x)。
只要这个h(x)是充分必要的,那么就可以作为hash的一个路径
hash的常用方式:
https://www.dotcpp.com/course/1056
这里再补充个:(亦或)
const ull mask=rand();
vector<int>mp[55];
ull shift(ull x) {
x ^= mask;
x ^= x << 13;
x ^= x >> 7;
x ^= x << 17;
x ^= mask;
return x;
}
map<ull, int> trees;
void gethash(int x){
sub[x]=1;
for(int i=0;i<mp[x].size();i++){
int to=mp[x][i];
gethash(to);
sub[x]+=shift(sub[to]);
}
}
void getroot(int x){
for(int i=0;i<mp[x].size();i++){
int to=mp[x][i];
rt[to]=sub[to]+shift(rt[x] - shift(sub[to]));
getroot(to);
}
}