526互联

【算法设计与分析】(一)序言：最大子数组、归纳法正确性证明、渐进记号。苏大计科院研一期末复习笔记

发布时间 2024-01-07 13:22:12作者: hotaru蛍

 

写在前面

 

首先，本人很菜。

 

其次，本文只也许够应付考试，个人使用。而且其实就是ppt内容只是我自己喜欢这样整理。虽然全力理解内容且认真书写但也可能存在错误，如有发现麻烦指正，谢谢?

 

最后，因为不知道考试怎么考，本人的复习方式是照着目录讲一遍自己的理解+写伪代码（如果来的及会再做一个综合纯享版），再做一下上课讲过的例题和作业(印象里只有主定理、FFT、网络流上课练习+分治和动规两次作业)。

 

文章持续更新中，链接在此：算法设计与分析 - 随笔分类 - hotaru蛍 - 博客园 (cnblogs.com)，或许考前能发完也可能发不完。

 

祝我们好运?

 

 

序言

（一）问题引入：最大子数组

问题定义：给定n个整数组成的数组a[1...n]，求其所有元素的和最大的子数组。（连续） 
如果数组元素都为负，定义最大和为0。

  1. 穷举

    1. 　计算所有的子数组的和找最大

    2. 　优化：求和的过程有重复可以复用

  2. 归纳法

  1. 归纳法思路
    1. 　基本情况：问题足够小可以直接求解
    2.     归纳步骤：建立小问题和大问题之间的关系（递归关系）
  2. 本问题应用归纳
    1. 　考虑问题划分：可以讲数组分为两个部分，问题就变成了求左半最大、右半最大、跨分界线最大的三部分之中的最大。
      　可以将原问题表示成：OPT(a[1...n])=max(OPT(left),OPT(right),S(Cross)) 
          需要注意S(Cross)并不是子问题。
    2.    考虑如何划分：
      1.   均匀划分：取 m= (1+n)/2 向下取整
        1. 　考虑  Cross：a[ i , j ]
          a[ i ... m ]总是以a[m]结尾的最大子数组
          a[ m+1 ... j ]总是以a[m+1]开头的最大子数组
          故计算方法就分别从a[m]和a[m+1]开始向两侧扫描

           

      2.   不均匀划分：分成a[1 2 ... n-1 ]和a[n],优化：不需从头计算L(1, n)

         

  3. 递归关系(动规)

                

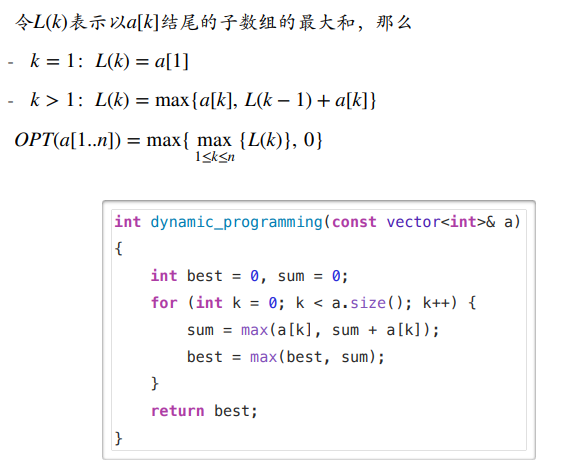
　　　4. 最大子数组方案总结

算法 算法描述 关键代码 时间复杂度 计算
brute_force 列举所有的子数组作比较 O(n^3)  
brute_force_opt 在循环过程中可以基于上一次结果计算做简单的优化 O(n^2)  
divide_and_conquer

归纳法①均匀划分：将数组分为两半，问题转化为求解OPT(a[1...n])=max(OPT(left),OPT(right),S(Cross)) ，其中S(Cross)通过分别向中心左右扫描得到。

 O(n log n) T(n) = 2T(n/2) + O(n) ⇒ T(n) = O(n log n)
divde_and_conquer_imba

归纳法②不均匀划分：将数组分成一个数和剩下的数，求解式同上，

 O(n^2) T(n) = T(n − 1) + O(n) ⇒ T(n) = O(n^2)
divde_and_conquer_imba_opt

不需从头计算L(1, n)其中S(Cross)通过可通过递归求解：基本情况是a[0]，其他时候返回max(L[n-1]+a[n] , a[n]) 

 

 O(n) T(n) = T(n − 1) + O(1) ⇒ T(n) = O(n)
dynamic_programming 重新定义问题：L(k)表示以a[k]结尾的子数组的最大和，基本情况为L(1)=a[1]，其他情况L(k) = max{ a[k] , L(k-1)+a[k] } O(n)  

（二）动规算法正确性证明

对于基于归纳的算法，可以用数学归纳法证明正确性。

  1. 假设对于某个整数k算法能够正确计算 ①L(k) ②best
  2. 基本情况：k=1，算法执行完毕后L(1)=a[1]，best=max{a[1],0}显然正确
  3. 归纳证明对于正整数k+1算法能够正确计算①L(k+1) ②best
    1. 令以a[k+1]结尾的最大子数组是a[ i ... k+1],i<=k+1.
    2. 若i<k+1，那么a[i...k]一定是以a[k]结尾的最大子数组，解为L(k)
    3. 故max{ a[k+1] , L(k)+a[k+1] }能够正确求解L(k+1)
    4. 得证算法能够对于正整数k+1算法能够正确计算①L(k+1) ②best
  4. 证毕。

（三）渐进记号

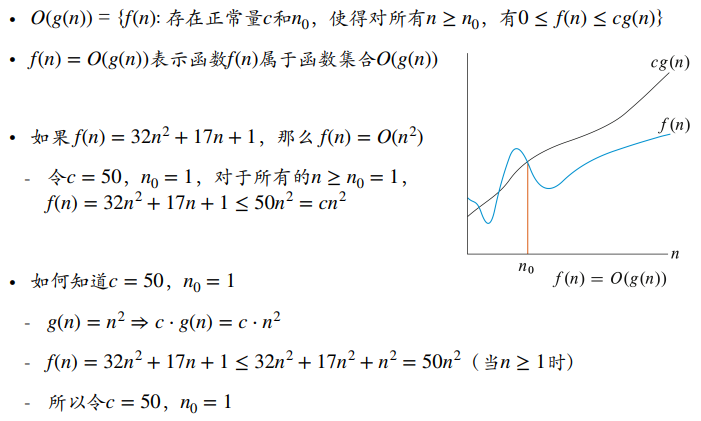
　　1. O记号 fn在下

  • 例： f(n)=32n^2+17n+1

  2. Ω记号 fn在上

  • 例 f(n)=2n^3-7n+1

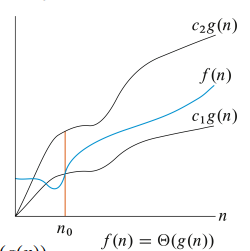
  3. Θ记号 fn在中

  • 例 f(n)=32n^2+17n+1

4. 等式中的渐进记号