前言

这一次思维训练，我感觉到了巨佬们的强大，也感受到了我与巨佬们的差距。

A	B	C	D	E	F
√	√	√	√	✖	√

A

Problem

给定一个长度为 $n$ 的序列 $a(a_i\in\{0,1\})$。$0$ 为空，$1$ 为非空。

现在有一种操作：将 $i$ 上的 $1$ 与 $i + 2$ 或 $i-2$ 上的 $0$ 互换，但 $i+1$，$i-1$ 必须为 $1$。

求序列可能达到的状态数。

Solve

显然，两个连续的 $1$ 是可以捆绑在一起计算的，偶数个连续的 $1$ 可以看作若干个两个连续的 $1$ .

这样只要考虑”落单的”奇数个 $1$ 就行了。

对于一个落单的 $1$，它可能会在某个时刻被两个连续的 $1$ 推着走，像这样：

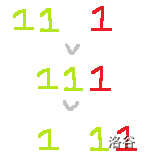
红色的 $1$ 为之前落单的 $1$。

但是这样就会变被很复杂。

换一种思路，不是 $11$ 推着 $1$ 走，而是 $1$ 与 $11$ 互换了位置。这样，落单的 $1$ 的贡献完全取决与 $11$ 的贡献。换句话说，把落单的 $1$ 连着位置一起去掉与原答案等效。

所以只要统计捆绑起来的 $11$ 在对应位置上的排列组合就行了。

设两个连续的 $1$ 的个数为 $x$，落单的 $1$ 的个数为 $y$，序列长度为 $n$，则答案为 $C_{n-x-y}^{x}$.

Code

#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 998244353

using namespace std;

inline int read() {
  rint x=0,f=1;char ch=getchar();
  while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
  while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
  return x*f;
}

void print(int x){
  if(x<0){putchar('-');x=-x;}
  if(x>9){print(x/10);putchar(x%10+'0');}
  else putchar(x+'0');
  return;
}

const int N = 2e5 + 10;

int inv[N], fac[N], n;

char a[N]; 

int qpow(int a, int b) {
  int res = 1;
  while(b) {
    if(b & 1) res = (res % mod * a % mod) % mod;
    a = (a % mod * a % mod) % mod, b >>= 1; 
  }
  return res;
}

int C(int m, int n) {
  return fac[n] * inv[m] % mod * inv[n-m] % mod;
}

void solve() {
  scanf("%d%s", &n, a + 1);
  int num1 = 0, num2 = 0, i = 1;
  for (; i <= n; i++) {
    if(a[i] == '1' && a[i+1] == '1') num1++, i++;
    else if(a[i] == '0') num2++;
  }
  cout << C(num1, num1 + num2) << '\n';
  return ;
} 

signed main() {
  fac[0] = inv[0] = fac[1] = inv[1] = 1;
  For(i,2,N-10) {
    fac[i] = (fac[i-1] % mod * i % mod) % mod;
    inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
  }
  For(i,2,N-10) {
    inv[i] = inv[i-1] * inv[i] % mod; 
  }
  int Q = read();
  while(Q--) {
    solve(); 
  } 
  return 0;
}

时间复杂度 $O(n)$（如果没有线性求逆元，那么时间复杂度为 $O(n\log n)$）。

B

Problem

给定一个 $0\dots L$ 的数轴，有 $n$ 个奶牛在数轴上，位置为 $x_i$，速度为 $d_i\in\{1,-1\}$，体重为 $w_i\in[1,10^3]$。

有两种事件：

奶牛 $i$ 移动到了 $0$ 或 $L$ 点，则停止运动，并做 $w_i$ 的体重贡献；
当奶牛 $i$ 和奶牛 $j$ 占据了相同点，则互换速度。奶牛可能在一个非整数点相遇；

令 $T$ 等于停止移动的奶牛（由于到达两个牛棚之一）的重量之和至少等于所有奶牛的重量之和的一半的最早时刻。请求出在时刻 $0\dots T$ 之间发生的奶牛相遇次数。

Solve

考虑将问题化简：两个奶牛相遇时，对穿并且互换体重。这样与原问题等价，但更好处理。

考虑一个奶牛 $i$ 到达终点时的重量贡献。由于速度一定，不会出现奶牛追及问题。这样在进行多轮体重互换后，对奶牛 $i$ 的体重有影响的奶牛只有一个。

假设这个奶牛的为 $j$，则奶牛 $j$ 的方向与奶牛 $i$ 的方向相反（这是必然的）。此时奶牛 $i$ 到达终点使的贡献为 $w_{j-d}$，其中 $d$ 为 $[i+1,j]$ 中与奶牛 $i$ 方向相同的奶牛数量。（不会证明，手玩出来是这样）。

计算出每一个奶牛到牛棚的距离，由于奶牛的运动方向恒定，所以对于每一个奶牛都有唯一的终点。然后对于每一个先到终点的奶牛，计算该奶牛的贡献。这里是 $O(n\log n)$ 的（因为可以用优先队列优化模拟过程，每一次取的奶牛肯定是最先到的，即离终点距离最短的。每一次从优先队列里取出离终点距离最短的奶牛计算）。

这样就可以计算出 $T$，然后在枚举所有奶牛，对于方向为左的奶牛，去寻找其他的方向为右的奶牛对冲。如果能冲到，则计数器加一。

总时间复杂度 $O(n\log n)$.

Code

#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;

using namespace std;

inline int read() {
  rint x=0,f=1;char ch=getchar();
  while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
  while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
  return x*f;
}

void print(int x){
  if(x<0){putchar('-');x=-x;}
  if(x>9){print(x/10);putchar(x%10+'0');}
  else putchar(x+'0');
  return;
}

const int N = 1e5 + 10;

struct Node {
  int w, x, d;
} a[N];

struct node {
  int id, x, d;
  bool operator < (const node &a) const {
    return a.x < x;
  } 
};

int n, l, now, s1[N], s2[N], laL, laR, Q[N], ans, sum, T;

priority_queue<node> q;

bool cmp(Node x, Node y) {
  return x.x < y.x;
}

signed main() {
  n = read(), l = read();
  For(i,1,n) a[i] = (Node) {read(), read(), read()};
  sort(a + 1, a + n + 1, cmp);
  For(i,1,n) {
    q.push((node){i, (a[i].d == 1 ? l - a[i].x : a[i].x), a[i].d});
    s1[i] = s1[i-1] + (a[i].d == 1), s2[i] = s2[i-1] + (a[i].d == -1);
    sum += a[i].w;
  }
  FOR(i,n,1) {
    if(a[i].d == 1) laL = i;
  }
  For(i,1,n) {
    if(a[i].d == -1) laR = i;
  }
  while(!q.empty()) {
    int id = q.top().id, x = q.top().x, d = q.top().d;
    q.pop();
    int dis = (d == 1 ? s1[laR] - s1[id] : s2[id-1] - s2[laL-1]);
    T = x;
    if(d == 1) {
      now += a[laR - dis].w;
    } else {
      now += a[laL + dis].w;
    }
    if(now * 2 >= sum) break;
  }
  int h = 1, t = 0;
  For(i,1,n) {
    if(a[i].d == 1) Q[++t] = i;
    else {
      while(h <= t && a[i].x - a[Q[h]].x > 2 * T) h++;
      ans += t - h + 1;
    }
  }
  cout << ans << '\n';
  return 0;
}

C

Problem

有一个 $n$ 个节点的树，现在可以将树改造，删去一条边，再加上一条边，问有多少个节点可能成为数树的重心（即其子数大小都不大于节点总数的一半）。

Solve

一眼换根 $dp$。

每一次我的操作肯定是想要树更胖，即根节点更有可能成为重心。

考虑求出这棵树改哪个子树上的边能使其更胖。

首先这棵子树一定要合法，并且它的大小要最大。

注意 $dp$ 的时候要算父辈节点的子树（因为是以不同的树为根而言）。

然后考虑换根 $dp$，最后判断边加边以后能否使其成为重心。

当然还有一个细节，定义以 $u$ 为根，儿子为 $v$，当最胖的子树就为子树 $v$ 本身时，断边加边操作无效，则需启用次大子树操作。所以维护 $dp$ 的最大次大值即可。

Code

#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007

using namespace std;

inline int read() {
  rint x=0,f=1;char ch=getchar();
  while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
  while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
  return x*f;
}

void print(int x){
  if(x<0){putchar('-');x=-x;}
  if(x>9){print(x/10);putchar(x%10+'0');}
  else putchar(x+'0');
  return;
}

const int N = 1e6 + 10;

struct Node {
  int v, nx;
} e[N << 1];

int n, h[N], tot, siz[N], Max[N][2], rt, cut[N], ans[N];

void add(int u, int v) {
  e[++tot].v = v, e[tot].nx = h[u], h[u] = tot;
}

void dfs1(int x, int fa) {
  siz[x] = 1;
  bool f = 1;
  for (int i = h[x]; i; i = e[i].nx) {
    int y = e[i].v;
    if(y == fa) continue;
    dfs1(y, x);
    siz[x] += siz[y];
    if(siz[y] > n / 2) f = 0;
  } 
  if(n - siz[x] > n / 2) f = 0;
  if(f) rt = x;
}

void dfs2(int x, int fa) {
  siz[x] = 1;
  for (int i = h[x]; i; i = e[i].nx) {
    int y = e[i].v;
    if(y == fa) continue;
    dfs2(y, x);
    siz[x] += siz[y];
    if(siz[y] > n / 2) continue;
    if(siz[y] > Max[x][0]) Max[x][1] = Max[x][0], Max[x][0] = siz[y];
    else if(siz[y] > Max[x][1]) Max[x][1] = siz[y];   
  }
}

void dfs3(int x, int fa, int maxn) {
  cut[x] = maxn;
  for (int i = h[x]; i; i = e[i].nx) {
    int y = e[i].v;
    if(y == fa) continue;
    if(n - siz[x] <= n / 2) maxn = max(maxn, n - siz[x]);
    if(Max[x][0] == siz[y]) dfs3(y, x, max(maxn, Max[x][1]));
    else dfs3(y, x, max(maxn, Max[x][0]));
  } 
  if(n - siz[x] - cut[x] <= n / 2 || x == rt) ans[x] = 1;
}

signed main() {
  n = read();
  For(i,1,n-1) {
    int u = read(), v = read();
    add(u, v); add(v, u);
  }
  dfs1(1, 0);
  dfs2(rt, 0);
  dfs3(rt, 0, 0);
  For(i,1,n) cout << ans[i] << ' ';
  return 0;
}

D

Problem

给定一张有向简单图，给定邻接矩阵，求长度为 $k$ 的路径条数，答案对 $10^9+7$ 取模。

Solve

不会啊~

Code

不会啊~

E

Problem

对于一个长度为 $len$ 的序列，它的答案定义为最小划分的组数（以使得每个组中的数两两乘积为平方数）。

给你一个长度为 $n(1\leq n \leq 5000)$ 的数组 $a_i(-10^8 \leq a_i \leq 10^8)$。对于其所有的子串，第 $k$ 个输出的数是答案为 $k$ 的子串的数量。

Solve

可以证明，$ab=n^2,cb=m^2$，则 $ac=k^2(a,b,c,n,m,k\in\mathbb{Z^{*}})$。

证明：

\[\begin{aligned} \because &a = p_{1}^{A_1}p_{2}^{A_2}p_{3}^{A_3}\dots p_{x}^{A_k}\\ &b=p_{1}^{B_1}p_{2}^{B_2}p_{3}^{B_3}\dots p_{x}^{B_k}\\ &c=p_{1}^{C_1}p_{2}^{C_2}p_{3}^{C_3}\dots p_{x}^{C_k}\\ \\ \therefore &A_1 + B_1\equiv0\pmod{2}\\ &A_2 + B_2\equiv0\pmod{2}\\ &A_3 + B_3\equiv0\pmod{2}\\ &\dots\\ &A_k + B_k\equiv0\pmod{2}\\ \\ \therefore &C_1 + B_1\equiv0\pmod{2}\\ &C_2 + B_2\equiv0\pmod{2}\\ &C_3 + B_3\equiv0\pmod{2}\\ &\dots\\ &C_k + B_k\equiv0\pmod{2}\\ \\ \therefore &A_1 + C_1\equiv0\pmod{2}\\ &A_2 + C_2\equiv0\pmod{2}\\ &A_3 + C_3\equiv0\pmod{2}\\ &\dots\\ &A_k + C_k\equiv0\pmod{2}\\ \end{aligned} \]

所以 $ab=n^2,cb=m^2$，则 $ac=k^2(a,b,c,n,m,k\in\mathbb{Z^{*}})$。

有了这一个结论，直接暴力将 $a_i\times a_j$ 插入并查集，然后暴力枚举每一个区间，统计区间内集合数。

记得开 long long。

Code

#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007

using namespace std;

inline int read() {
  rint x=0,f=1;char ch=getchar();
  while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
  while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
  return x*f;
}

void print(int x){
  if(x<0){putchar('-');x=-x;}
  if(x>9){print(x/10);putchar(x%10+'0');}
  else putchar(x+'0');
  return;
}

const int N = 5e3 + 10;

int n, x[N], f[N], num[N], ans[N];

int find(int x) {
  return (x == f[x] ? x : f[x] = find(f[x]));
}

void merge(int x, int y) {
  f[find(x)] = find(y);
}

signed main() {
  n = read();
  For(i,1,n) x[i] = read(), f[i] = i;
  For(i,1,n) {
    For(j,i+1,n) {
      if(x[i] * x[j] > 0) {
        int tmp = sqrt(x[i] * x[j]);
        if(tmp * tmp == x[i] * x[j]) {
          merge(i, j); 
        }
      }
    }
  }
  int tot = 0;
  For(i,1,n) {
    tot = 0;
    memset(num, 0, sizeof num);
    For(j,i,n) {
      if(!x[j]) ans[max(1ll, tot)]++;
      else {
        if(!num[find(j)]) {
          num[find(j)] = 1; tot++;
        }
        ans[tot]++; 
      }
    }
  }
  For(i,1,n) cout << ans[i] << ' '; 
  return 0;
}

F

Problem

给定一个正整数序列 $a$，计算有多少个正整数数列 $b$ ，满足：

$1 \le b_i \le a_i,i\in[1,n]$；
$b_i\not= b_{i+1},i\in[1,n)$；

答案对 $998244353$ 取模。

Solve

显然，在决策第 $i$ 项时，前 $i-1$ 项不会受到影响，无后效性，考虑 $dp$。

设 $dp_{i,j}$ 表示前 $i$ 项，第 $i$ 项为 $j$ 的合法方案数。

递推式为：

\[dp_{i,j} = \sum\limits_{1\le k\le a_{i-1},k\not=j}^{}dp_{i-1,k} \]

答案为 $ \sum\limits_{k\in[1,a_n]} dp_{i,k}$。

发现 $i$ 那一维可以滚动数组。（滚动数组用完一维就要清空一维）（不给递推式了）

但是时空双炸，然后就推进不下去了。

换一种思路，考虑容斥，称满足 $b_i=b_{i+1}(i\le i<n)$ 的 $i$ 为关键点。则答案为关键点为 $0$ 的 $\{b_n\}$ 的数量，假设有 $i$ 个关键点时的 $\{b_n\}$ 数量为 $r_i$，则有：

\[r_n=\sum\limits_{i=0}^{n-1}(-1)^{i}r_i \]

发现对于长度为 $n$ 的 $\{b_n\}$，至少有 $k$ 个关键点的一组 $\{b_n\}$ 其实是将整个数组分成了连续 $n-k$ 段，每段的 $b_i$ 一定相同，再次考虑 $dp$。

设 $f_{i,0/1}$ 表示在 $b_1,\dots b_i$ 这一段排列，分成连续的偶数段或奇数段的方案数，每段的 $b_i$ 一定相同。

则有：

\[f_{i,0/1}=\sum\limits_{j=1}^{i}f_{j-1,0/1}(\min\limits_{k=j}^ia_k) \]

这里的 $\min\limits_{k=j}^ia_k$ 的含义为 $b_j,\dots,b_i$ 这些数只能是同一个数，所以是取最小值。

转移时间复杂度为 $O(n^2)$ ，不过可以使用单调栈优化。

找到从 $i$ 向左看第一个小于 $a_i$ 的数 $a_x$，则有：

\[f_{i,0/1}=f_{x,0/1}+a_i\sum\limits_{j=x+1}^{i}f_{j-1,0/1} \]

因为 $a_x$ 为从 $i$ 向左看第一个比 $a_i$ 小的数，所以有 $\min\limits_{k=j}^ia_k$ 与 $\min\limits_{k=j}^xa_k$ 相等，所以这些 $j$ 的贡献等价于 $f_{x,0/1}$。

由于 $a_{x+1},a_{x+1},\dots,a_{i-1}$ 都比 $a_i$ 大，所以对于任意的 $j(j\in[x+1,i])$，都有 $\min\limits_{k=j}^ia_k=a_i$，这些 $j$ 的答案贡献之和为 $a_i\sum\limits_{j=x+1}^{i}f_{j-1,0/1}$。

这些操作可以通过单调栈来实现。

边界：$f_{0,0}=1,f_{0,1}=0$。时间复杂度 $O(n)$。

Code

#include <bits/stdc++.h>
#define int long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 998244353

using namespace std;

inline int read() {
  rint x=0,f=1;char ch=getchar();
  while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
  while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
  return x*f;
}

void print(int x){
  if(x<0){putchar('-');x=-x;}
  if(x>9){print(x/10);putchar(x%10+'0');}
  else putchar(x+'0');
  return;
}

const int N = 2e5 + 10;

int n, a[N], stk[N], f[N][2], s[N][2], top;

signed main() {
  n = read();
  For(i,1,n) a[i] = read();
  f[0][0] = s[0][0] = 1;
  For(i,1,n) {
    while(top && a[stk[top]] >= a[i]) top--;
    f[i][0] = ((top == 0 ? 0 : f[stk[top]][0]) % mod + (s[i-1][1] - (top == 0 ? 0 : s[stk[top]-1][1]) + mod) * a[i]) % mod;
    f[i][1] = ((top == 0 ? 0 : f[stk[top]][1]) % mod + (s[i-1][0] - (top == 0 ? 0 : s[stk[top]-1][0]) + mod) * a[i]) % mod;
    s[i][0] = (s[i-1][0] + f[i][0]) % mod;
    s[i][1] = (s[i-1][1] + f[i][1]) % mod;
    stk[++top] = i;
  }
  cout << ((n & 1 ? mod - 1 : 1) * (f[n][0] - f[n][1] + mod) % mod) % mod; 
  return 0;
}