为什么使用PCA

从过拟合说起

在数据量小、数据维度高，模型较为复杂时，很容易产生过拟合。训练误差小而泛化误差较大被称为过拟合，而我们所追求的是泛化误差较小，为了解决过拟合问题，一般有以下的解决方案，一是最直接有效的方法，增加数据量，但是增加数据量成本一般较高，二是进行正则化，规范参数空间防止过拟合，三是进行降维。

解决过拟合问题的方法
- 增加数据量/数据扩增
- 正则化，如在损失函数中加入L1范数和L2范数
- 降维
  - 特征选择：过滤法、包装法和嵌入法
  - 线性降维：LDA、PCA
  - 非线性降维：流形

维度灾难

维度灾难，一般指在涉及到向量的计算的问题中，随着维数的增加，计算量呈指数倍增长的一种现象。在机器学习中，当数据的维度增加时，对于数据的需求量将会几何式增长。

下面尝试从几何的角度去理解维度灾难。在二维空间中，有一个边长为1的正方形，正方形有一个内切圆，相似的，在三维空间中，有一个边长为1的正方体，正方体有一个内接球，以此类推，超立方体和超球体的体积在各个维度中如下表所示

维度	超立方体体积	超球体体积
2	1	$k_2\pi(0.5)^2$
3	1	$k_3\pi(0.5)^3$
4	1	$k_4\pi(0.5)^4$
……	……	……
n	1	$k_n\pi(0.5)^n$

其中$k_i，i = 1，2，……，n$为常数，当n趋向于无穷时，超球体的体积将会趋近于0，也就是说，在高维空间中，超球体的内部是“空的”，大部分数据都分布在超球体和超立方体之间的“边边角角”中，这也就造成了数据样本的稀疏性，同时也会导致样本的空间分布不均匀，进而导致难以进行分类。从几何的角度我们会发现，很多我们在低维空间中的直觉在高维空间中是不work的。因此，面对特别高维的数据时，如果数据量不够大，我们会需要进行降维。

模型定义

PCA的两种推导

可以将PCA模型总结为“一个中心，两个基本点”

一个中心：原始特征空间的重构。PCA的核心是对特征空间进行重构，将原本相关的特征转化为互相正交。
两个基本点
- 最大投影方差：样本点在所求超平面上的投影尽可能分开
- 最小重构距离：样本点到所求超平面的距离都足够近

基于两种性质，能够得到主成分分析的两种等价推导。

数据准备

对于数据集$\{x_i,i=1,2...n\}$，$x_i$为p维向量，定义矩阵

\[X = (x_1,x_2,...,x_n)^T \]

定义样本均值矩阵

\[\begin{aligned} \bar{x}&=\frac{1}{n}\sum x_i\\ &=\frac{1}{n}\begin{pmatrix}x_1&x_2&...&x_n\end{pmatrix}\begin{pmatrix}1&1&...&1\end{pmatrix}^T\\ &=\frac{1}{n}X^T1_n \end{aligned} \]

其中$1_n=\begin{pmatrix}1&1&...&1\end{pmatrix}^T$

定义样本协方差矩阵

\[\begin{aligned} S=& \frac{1}{n}(x_i-\bar{x})(x_i-\bar{x})^T\\ &= \frac{1}{n} \begin{pmatrix} x_1-\bar{x}&x_2-\bar{x}&...&x_n-\bar{x} \end{pmatrix} \begin{pmatrix} x_1-\bar{x}&x_2-\bar{x}&...&x_n-\bar{x} \end{pmatrix}^T \end{aligned} \]

其中

\[\begin{aligned} &\begin{pmatrix} x_1-\bar{x}&x_2-\bar{x}&...&x_n-\bar{x} \end{pmatrix}\\ &=\begin{pmatrix} x_1&x_2&...&x_n \end{pmatrix}- \begin{pmatrix} \bar{x}&\bar{x}&...&\bar{x} \end{pmatrix} \\ &=X^T-\bar{x}\begin{pmatrix}1&1&...&1\end{pmatrix}\\ &= X^T-\frac{1}{n}X^T1_n1_n^T\\ &=X^T(I_n-\frac{1}{n}1_n1_n^T) \end{aligned} \]

则可知

\[\begin{aligned} S &= \frac{1}{n}X^T(I_n-\frac{1}{n}1_n1_n^T)(I_n-\frac{1}{n}1_n1_n^T)^TX\\ &=\frac{1}{n}X^TH_nH_n^TX \end{aligned} \]

其中$H_n = I_n-\frac{1}{n}1_n1_n^T$被称为中心矩阵，有如下性质

\[\begin{aligned} H_n = H_n^T\\ H_n^2=H_n \end{aligned} \]

则$$S = \frac{1}{n}X^TH_nX$$

最大投影方差

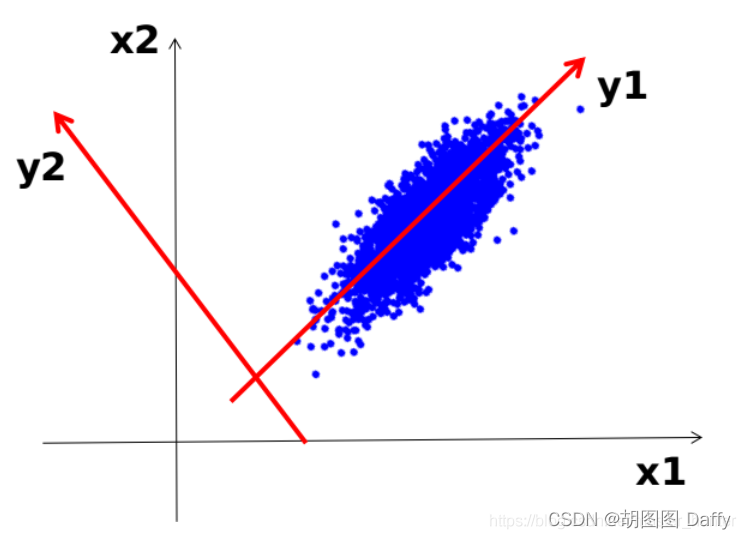
请添加图片描述
从最大投影方差角度去考虑，也即是说样本点在超平面上的投影应当尽可能分开，则应当使投影后样本方差最大化。如图，样本点投影到y_1方向后样本会较为分散，y_1方向就是我们所需要寻找的“主成分”。
记$w$为我们所要求的主成分方向，由于我们不需要考虑其长度，故可以先规定$w^Tw=1$，则中心化后的样本点$x_i$在$w$上的投影为$(x_i-\bar{x})^Tw$，则投影点的样本协方差矩阵为

\[\begin{aligned} J &= \frac{1}{n}\sum_{i=1}^{n}{[(x_i-\bar{x})^Tw]^2}\\ &=\frac{1}{n}\sum_{i=1}^{n}w^T(x_i-\bar{x})(x_i-\bar{x})^Tw\\ &=\frac{1}{n}w^T(\sum_{i=1}^{n}(x_i-\bar{x})(x_i-\bar{x})^T)w\\ &=\frac{1}{n}w^TSw \end{aligned} \]

则问题转化为求

\[\begin{aligned} &\hat{w} = \mathop{\mathrm{argmax}}\limits_{w}{w^TSw}\\ &\text{ s.t. } w^Tw = 1 \end{aligned} \]

使用拉格朗日乘子法求解该问题

\[\begin{aligned} L(w,\lambda) = w^TSw + \lambda (1-w^Tw)\\ \frac{\partial L}{\partial w}= 2Sw-2\lambda w=0\\ Sw = \lambda w \end{aligned} \]

观察最后得到的式子后我们不难发现，所求的$w$实际上就是样本协方差矩阵的特征向量，而$\lambda$则是对应的特征值而对该式子左右各左乘一个$w^T$后式子变成了

\[\begin{aligned} w^TSw& = \lambda w^Tw\\ J&=\lambda \end{aligned} \]

也即是说对于越大的特征值对应的特征向量，投影点样本协方差就越大，则可以根据特征值进行排序，确定主成分的顺位，保留排位靠前的主成分，进而实现降维。

最小重构距离

为表达方便，下面直接使用已经中心化后的数据，也即$\sum x_i=0$（我太懒了），记$W = \begin{pmatrix}w_1&w_2&...&w_d\end{pmatrix}$，其中$w_i$为重构特征空间后的坐标轴向量，且$w_i^Tw_i = 1$则对于每一个样本点，可以使用新坐标系进行重构，也即$x_i = \sum_{k=1}^{d}{(x_i^Tw_k)w_k}$，舍弃一些特征，只取$p$个特征则可得$\hat{x_i} = \sum_{k=1}^{p}{(x_i^Tw_k)w_k}$，则重构距离可以表示为

\[\begin{aligned} J &= \sum_{i = 1}^n\left \| x_i-\hat{x_i})\right \|^2 \\ &=\sum_{i = 1}^n\left \|\sum_{k=1}^{d}{(x_i^Tw_k)w_k}-\sum_{k=1}^{p}{(x_i^Tw_k)w_k}\right \|^2\\ &=\sum_{i = 1}^n\left \|\sum_{k=p+1}^{d}{(x_i^Tw_k)w_k}\right \|^2\\ \end{aligned} \]

对于$\left \|\sum_{k=p+1}^{d}{(x_i^Tw_k)w_k}\right \|$，该式子可视为在以$w_{p+1},w_{p+1},...,w_{d}$为基向量的坐标系中求向量$\begin{pmatrix}x_i^Tw_{p+1}&x_i^Tw_{p+2}&...&x_i^Tw_{n}\end{pmatrix}$的模长，则式子可改写为

\[\begin{aligned} J &= \sum_{i = 1}^n\sum_{k=p+1}^{d}(x_i^Tw_k)^2\\ &=\sum_{k=p+1}^{d}\sum_{i = 1}^nw_k^Tx_ix_i^Tw\\ &=n\sum_{k=p+1}^{d}w_k^TSw \end{aligned} \]

同样使用拉格朗日乘子法进行求解，将会得到与最大投影方差角度一样的结果

小结

PCA仅仅只需要保留$W^*$(大小排位靠前的特征值所对应的特征向量组成的矩阵)与样本均值向量（用于中心化），即可通过简单的矩阵减法和乘法将新样本投影到低维空间中去，尽管因舍弃了某些特征，导致低维空间与高维空间必然有所不同，会舍弃掉一部分信息，但是这是必要的，一方面，舍弃这部分信息后将使得样本信息密度增大，另一方面，数据受到噪音影响是，最小的特征值所对应的特征向量往往与噪音有关，将他们舍弃能够一定程度上起到去噪的效果。