blog。NOIP2023 T3,特殊性质题。
什么是特殊性质题?就是题目给出了你极其神秘的性质,从而引导你想出正解。
本篇题解将从部分分的角度,一步步讲述部分分与正解的关系。这样看的话,本题会变得十分简单。
\(\text{Task }1\sim7\),\(O(Tnm)\)
首先转换题意。\(\forall(f_i-g_i)(f_j-g_j)>0\),本质上就是满足两者中的一个:
- 所有 \(1\le i\le 10^{100}\) 都有 \(f_i<g_i\)。
- 所有 \(1\le i\le 10^{100}\) 都有 \(f_i>g_i\)。
这两件事情本质相同,我们只考虑第一件事情(\(\forall f_i<g_i\)),第二件事情就是将 \(f,g\) 对调一下再处理。
你想一想拓展的本质。其实就是有两个指针 \(X_i\) 与 \(Y_j\),每次如果有 \(X_i<Y_j\),那么可以做:
- \((i,j)\to(i+1,j)\),表示 \(f\) 的下一位是 \(X_{i+1}\),\(g\) 的下一位仍然是 \(Y_j\)。
- \((i,j)\to(i,j+1)\),表示 \(f\) 的下一位仍然是 \(X_{i}\),\(g\) 的下一位是 \(Y_{j+1}\)。
- \((i,j)\to(i+1,j+1)\),表示 \(f\) 的下一位是 \(X_{i+1}\),\(g\) 的下一位是 \(Y_{j+1}\)。
于是考虑 DP。\(dp_{i,j}\) 表示 \(X\) 匹配到第 \(i\) 位,\(Y\) 匹配到第 \(j\) 位,是否可行。转移即:
答案即 \(dp_{n,m}\)。这一部分的代码如下,时间复杂度 \(O(Tnm)\)。
#include <iostream>
#include <cstdio>
#include <cassert>
using namespace std;
const int N = 5e5 + 5;
bool dp[2005][2005];
bool chk(int x[], int y[], int n, int m) //是否可以构造出 fi<gi
{
if (x[1] <= y[1] || x[n] <= y[m]) return false;
for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) dp[i][j] = false;
dp[1][1] = true;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (x[i] > y[j]) dp[i][j] |= (dp[i - 1][j - 1] | dp[i - 1][j] | dp[i][j - 1]);
return dp[n][m];
}
int x[N], y[N], ttx[N], tty[N];
int main()
{
int n, m, q;
scanf("%*d%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i++) scanf("%d", &x[i]);
for (int i = 1; i <= m; i++) scanf("%d", &y[i]);
putchar(chk(x, y, n, m) || chk(y, x, m, n) ? '1' : '0');
while (q--)
{
for (int i = 1; i <= n; i++) ttx[i] = x[i];
for (int i = 1; i <= m; i++) tty[i] = y[i];
int cx, cy;
scanf("%d%d", &cx, &cy);
while (cx--) {int p, v; scanf("%d%d", &p, &v); ttx[p] = v;}
while (cy--) {int p, v; scanf("%d%d", &p, &v); tty[p] = v;}
putchar(chk(ttx, tty, n, m) || chk(tty, ttx, m, n) ? '1' : '0');
}
return 0;
}
\(\text{Task }8\sim14\),\(O(T(n+m))\) 特殊性质
考虑上面那个做法是在干啥。
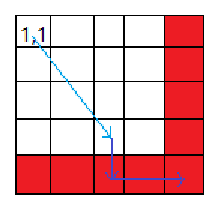
令 \(A_{i,j}=[X_i<Y_j]\),从 \((1,1)\) 开始,每次可以向右、下、右下的 \(A_{i,j}=1\) 的点走一步,问能否走到 \((n,m)\)。
首先,如果 \(X_{\min}\ge Y_{\min}\),说明 \(Y_{\min}\) 的那一列的全部 \(A_{i,j}\) 都是 \(0\)。显然路被堵死了,走不到捏。
同理,\(Y_{\max}\le X_{\max}\) 也是走不到。
考虑完这些小情况后,根据这个特殊性质,必然有:
- 对于 \(1\le i\le m\),都有 \(A_{n,i}=1\)。
- 对于 \(1\le i\le n\),都有 \(A_{i,m}=1\)。
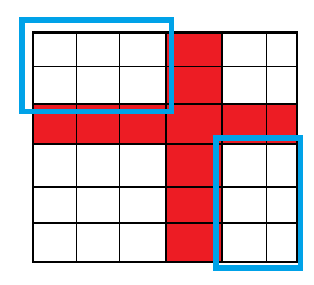
这说明,只要我们能走到第 \((n-1)\) 行或者第 \((m-1)\) 列,就一定能顺着这条通路到达 \((n,m)\)。看起来像下面这样:
以此类推,找到 \(1\sim(n-1)\) 的最小值,如果有 \(X_\min<Y_\min\),说明:对于 \(1\le i\le m-1\),都有 \(A_{xmin,i}=1\)。
这说明,只要我们能走到第 \(xmin\) 行或者第 \((m-1)\) 列,就一定能顺着这条通路到达第 \(n\) 行或者第 \(m\) 列,然后再到达 \((n,m)\)。
同样地,列也可以类似地操作。
可以理解为,现在有一个边框,你只要到达了边框就能走到 \((n,m)\) 了。那么每次缩小整个边框地大小,必然是不会更劣的。
于是你一直缩小边框,如果中途无法缩小(\(X_\min\ge Y_\min\) 且 \(Y_\max\le X_\max\)),不可行;否则,如果边框到达了 \((1,1)\),那么就是可行。
实现方面可以采用递归,维护前缀最小值 / 最大值的位置即可。时间复杂度 \(O(T(n+m))\)。
bool check(int x, int y)
{
if (x == 1 || y == 1) return true;
Node X = preX[x - 1], Y = preY[y - 1];
if (f[X.min] < g[Y.min]) return check(X.min, y);
if (g[Y.max] > f[X.max]) return check(x, Y.max);
return false;
}
正解
特殊性质的提示性非常强。你可以找到 \(X\) 的最小值与 \(Y\) 的最大值的位置。