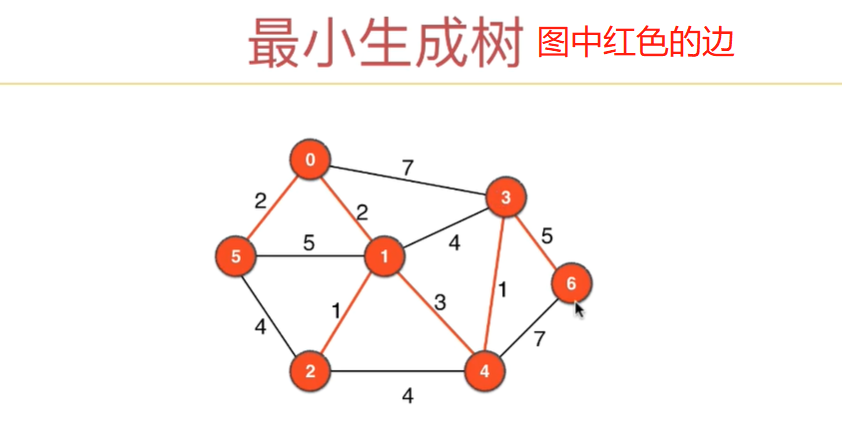
无向有权图之最小生成树问题
前10章我们讲解地都是无向无权图,本章我们将讲解无向有权图,以及无向有权图的经典问题:最小生成树问题(MST:Minimum Spanning Tree)
1~2 无向有权图的实现
主要是用TreeMap代替了无向无权图的TreeSet
本节用到的图
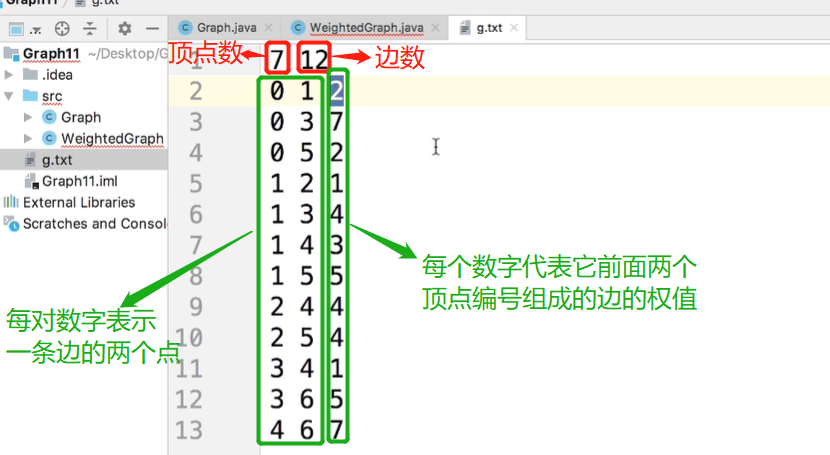
上面的graph.txt对应的图如下:
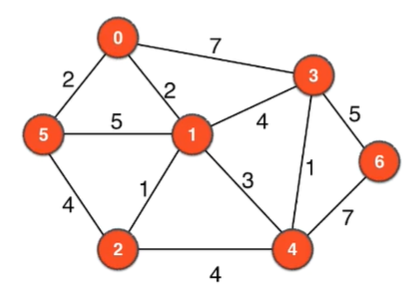
最终的代码
3 最小生成树和Kruskal算法
什么是生成树
用n-1条边把含有n个顶点的图连接起来就形成了图的生成树,一个图一般都有很多个不同的生成树

的两个生成树如下:
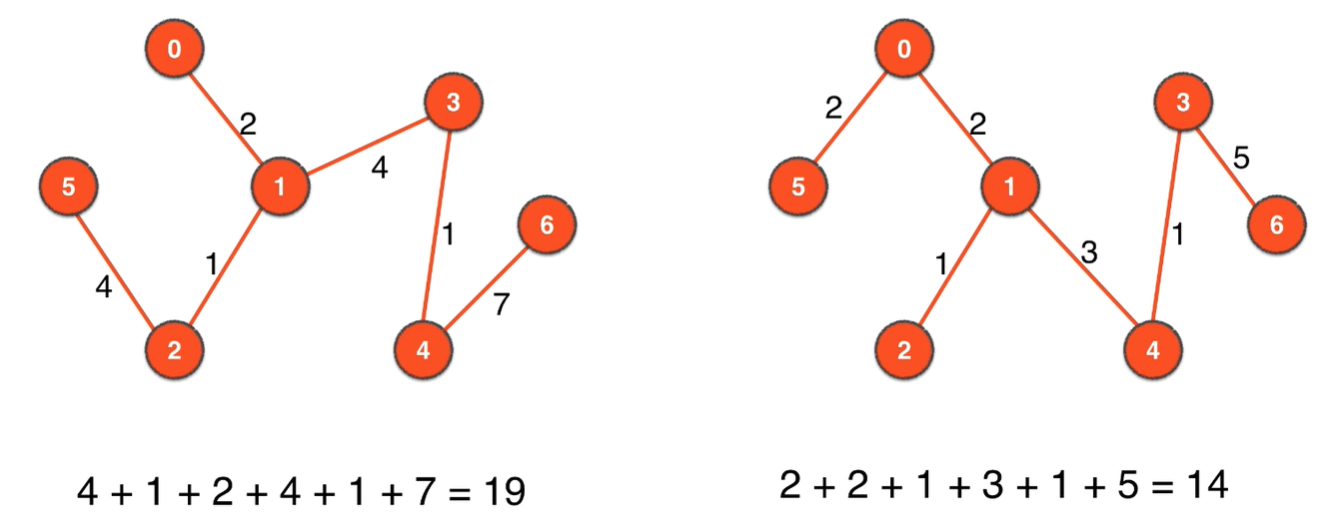
什么是最小生成树
在有权图中,不同的n-1条边形成的不同生成树其权总和一般也就不同,权值总和最小的就叫最小生成树
最小生成树的用途
- 布线设计
- 网络设计
- 电路设计
- 保证图联通且费用最低
求最小生成树的思想
把所有的边进行排序,基于贪心思想使用权值小的边,一旦选到的边使得图中有环就舍弃这条边,如此下去一直到选够n-1条边,这n-1条边组成的生成树就是最小生成树
上面的过程就是求最小生成树的Kruskal算法
4 Kruskal算法正确性的理论保证:切分定理
切分
把图中的顶点分为两部分,就称为一个
切分
如下面几个图都不同的颜色均组成一个切分
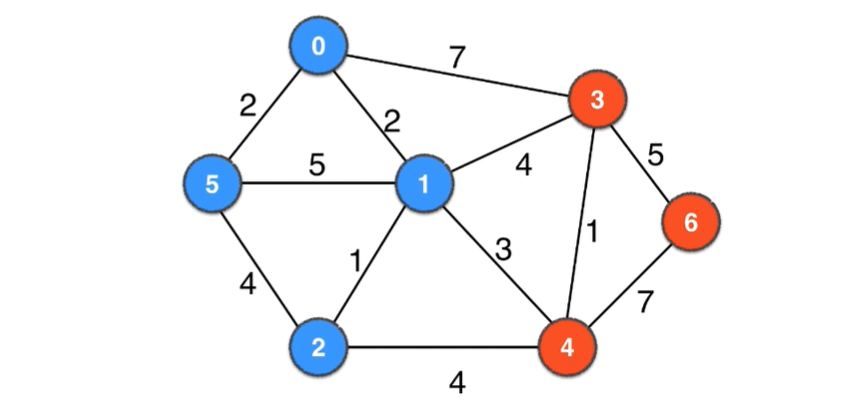
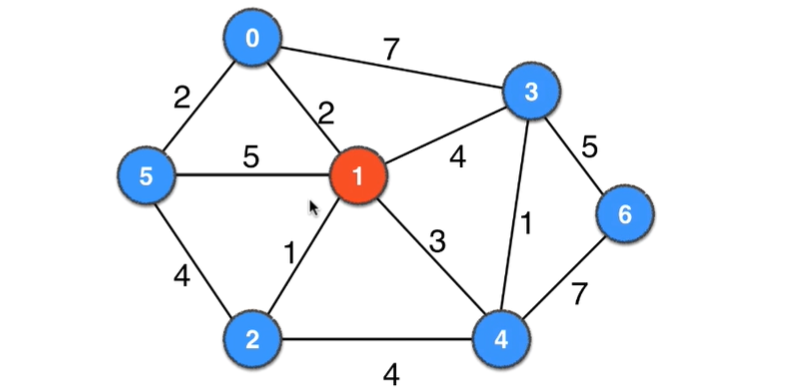
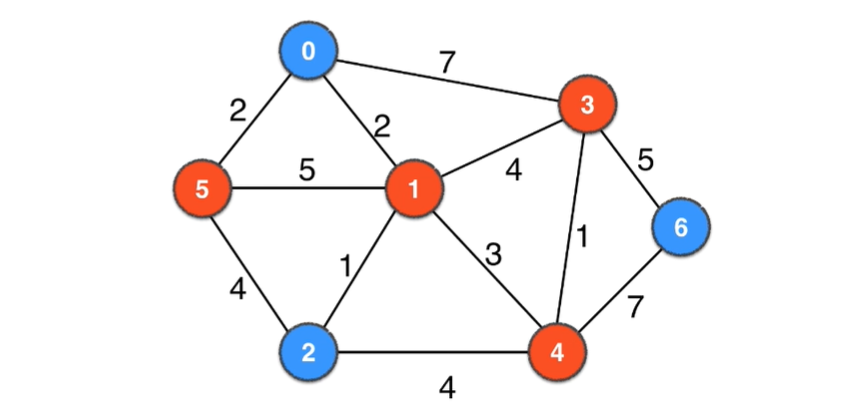
横切边
如果一个边的两个端点,属于
切分不同的两边,则这个边被称为横切边
下面是图的一种切分的横切边
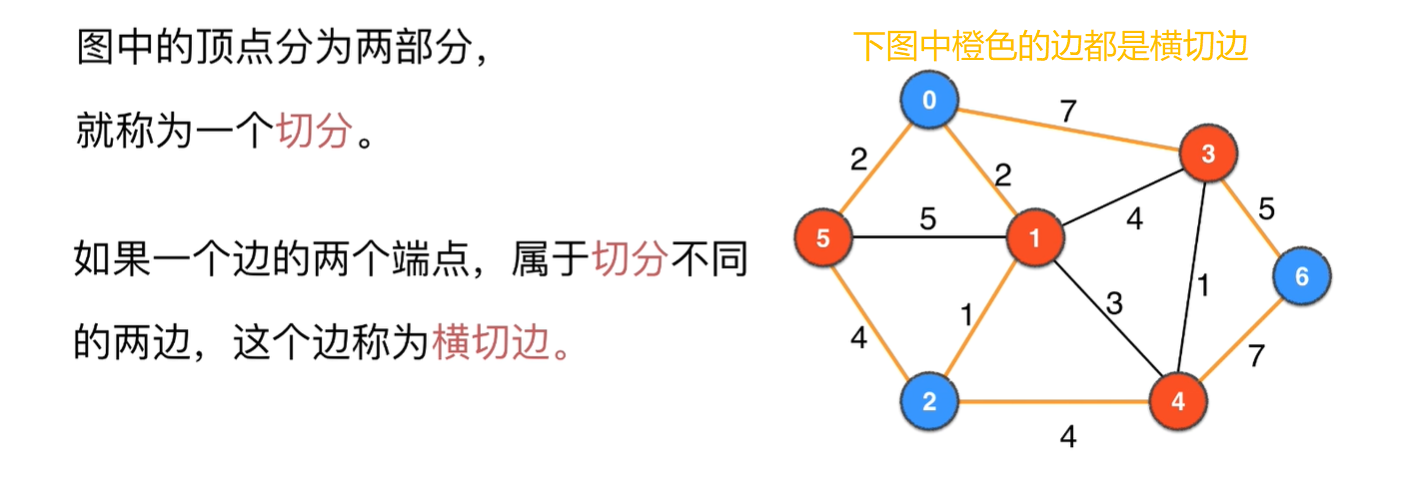
下面是图的另一个切分的横切边:
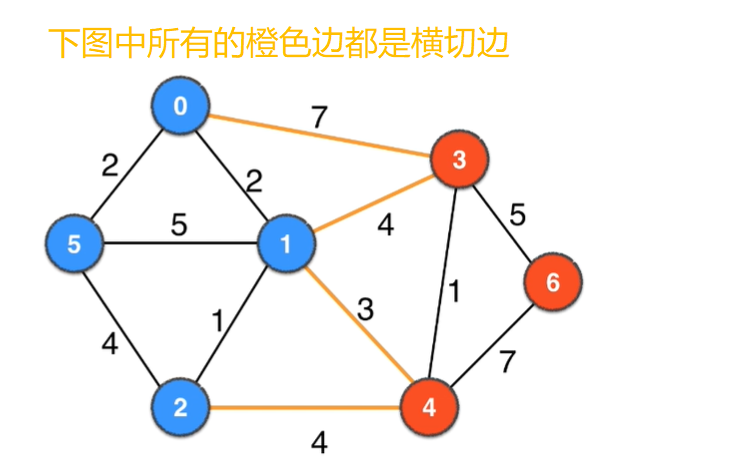
切分定理
横切边中的最短边,一定属于最小生成树
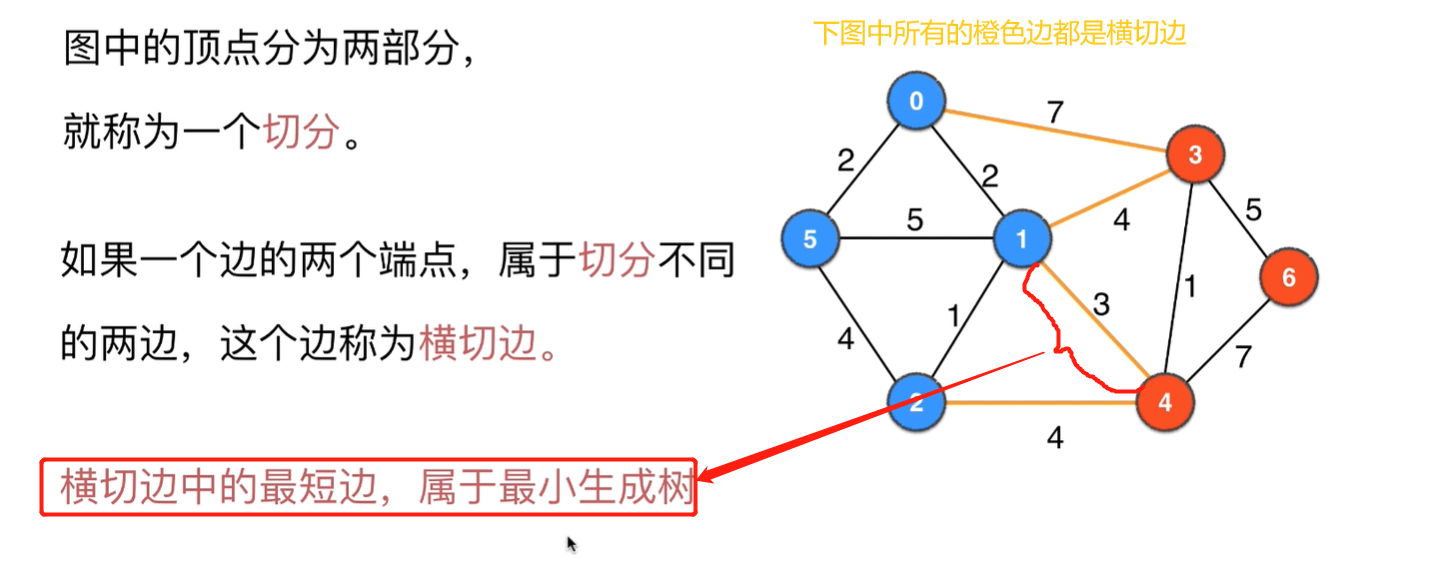
反证法证明:如下图,a、b、c是蓝红切分的所有横切边,红蓝里面的顶点和边加上a组成了最小生成树,a是a、b、c中权值最小的,假设a不是最小生成树的一条边,那么b、c中的一条可以代替a称为最小生成树的一部分(必须从横切边中选取一条才能使得蓝红两部分是联通地),但是b、c中任何一条加入,新的生成树的权值综合肯定大于替换a之前的,所以得证a一定是最小生成树的一条边
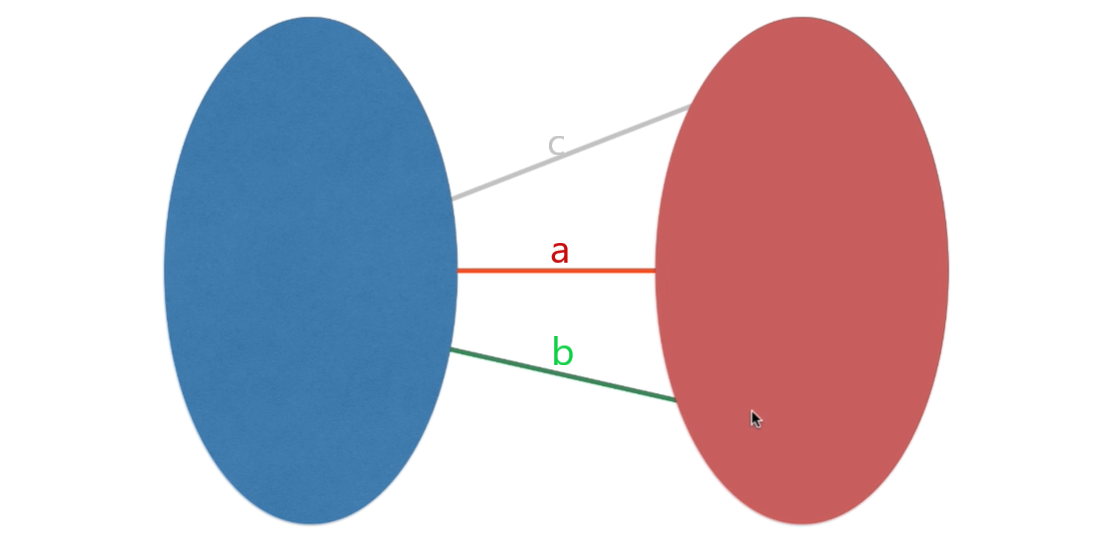
具体的例子可以见下图:
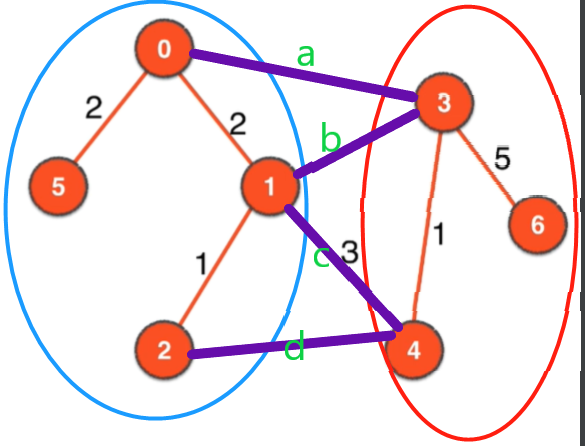
Kruskal算法与切分定理的关系
Kruskal算法每次选择一个最短边,如果这个边没有形成环:相当于是对一个切分,选择了最短横切边
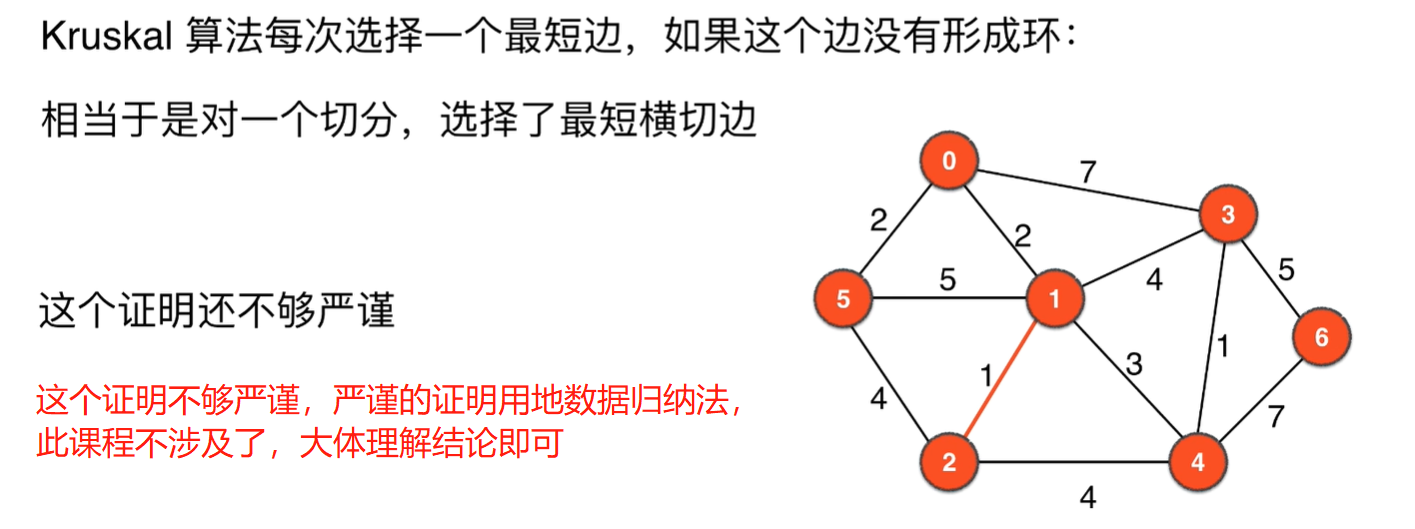
5~6 Kruskal算法实现
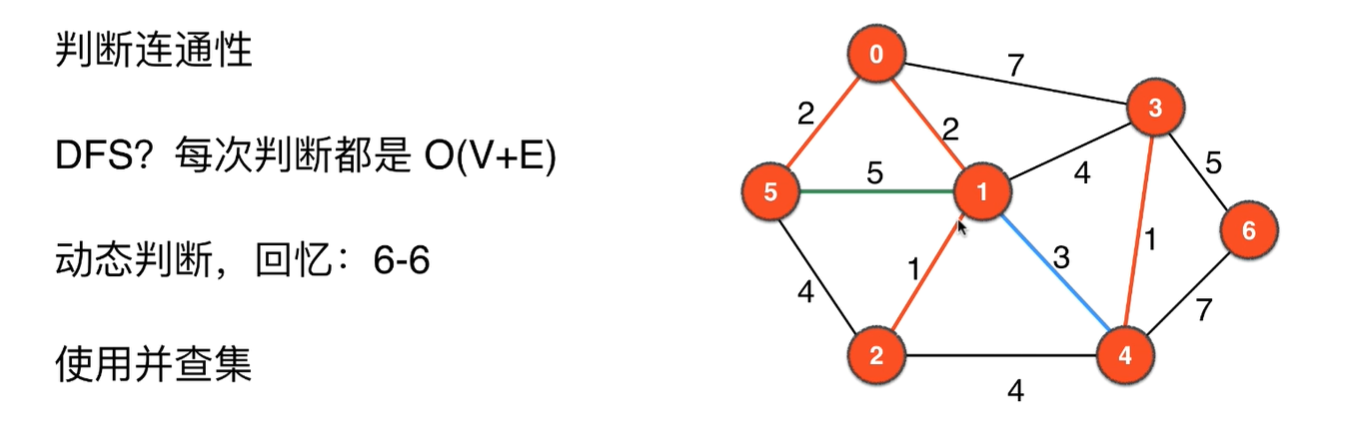
如何快算判断已有的边中是否有环
- DFS 每次判断的事件复杂度都是O(V+E),而且对动态变化的图性能不高
- 使用并查集:事件复杂度是O(E),而且支持动态变化的图很好。
所以我们使用并查集来实现已有边中是否有环的快速判断,思想如下:
之前已经加入地边都放到到一个并查集中,一个联通分量内的两个点在并查集中是true,如果我们要加入地边的两个端点在并查集中为true,那么这条边加入一定会生成环。
简而言之,kruskal算法新加入的边的两个顶点在并查集中必须为false,否则不能加入
并查集相关的只是可以参考
Kruskal算法实现
测试图如下:
Kruskal求最小生成的时间复杂度是O(ElogE)级别的
时间开销主要是在
Collections.sort(edges);上
7~9 Prim算法
回顾切分定理

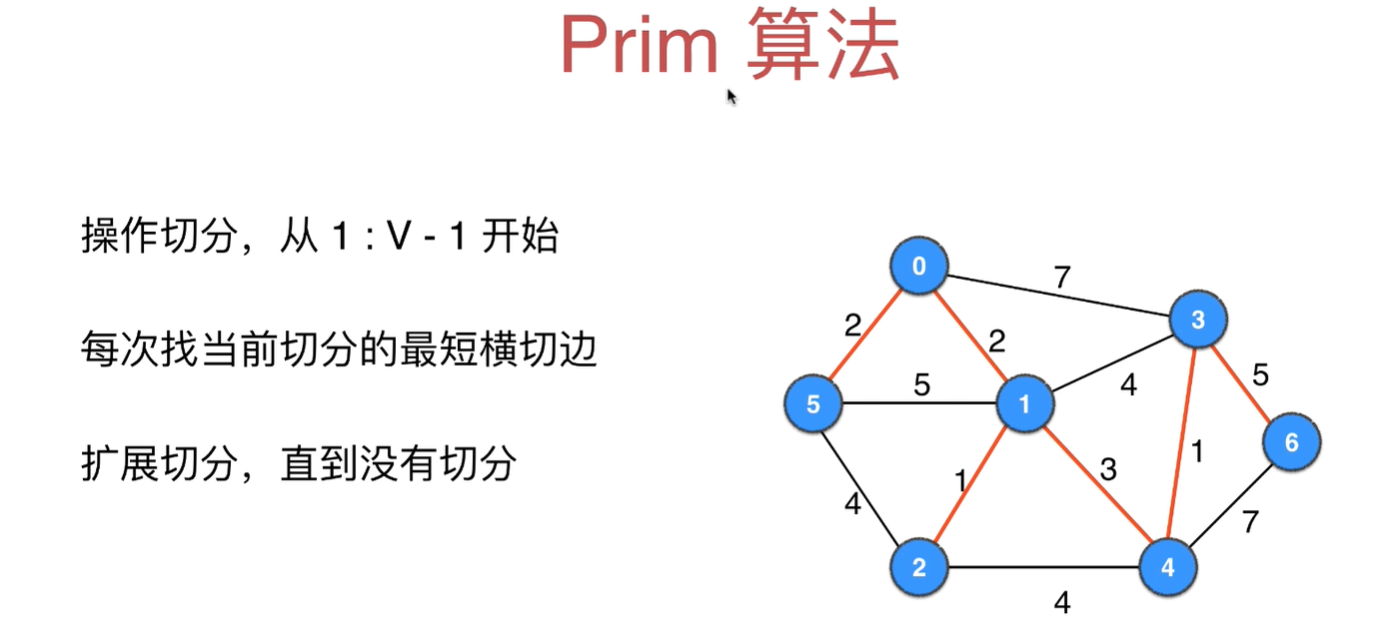
Prim算法的原理和过程模拟
按照顶点个数从(1, v-1)、(2, v-2)、.....不断划分切分,对每种切分都找最短横切边,最后横切边加入到mst列表中,就形成了最小生成树
详细过程模拟如下(@Todo):
Prim算法的事件复杂度:O(VE)
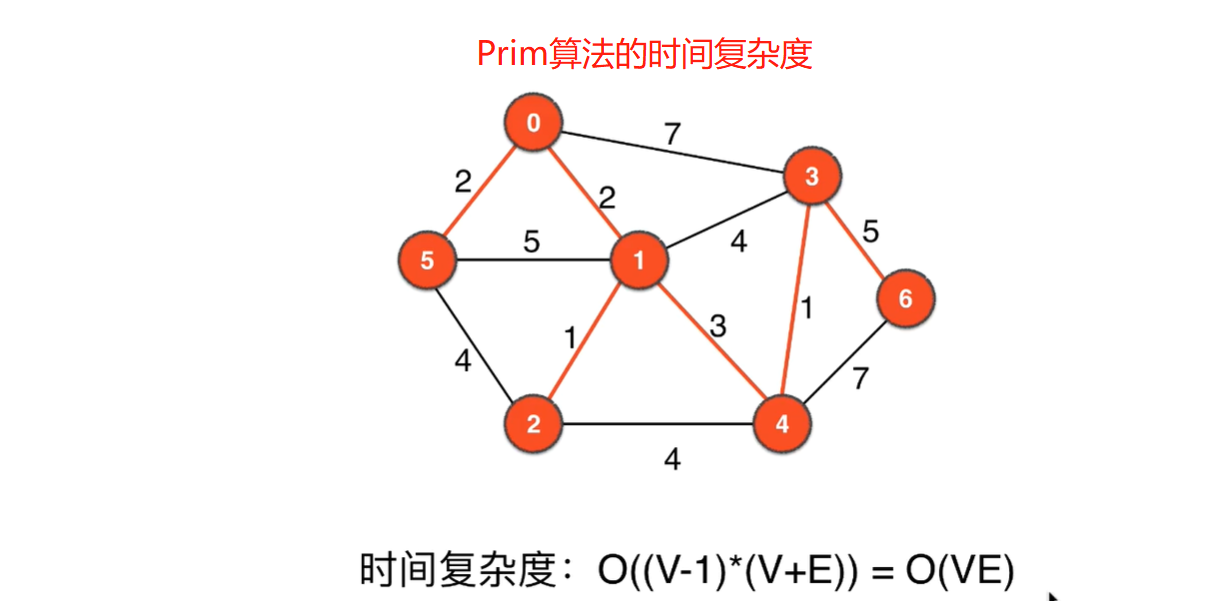
Prim算法优化
基于优先队列(最小堆)快速找到最小的横切边。优化后的算法时间复杂度和Kruskal一样是
O(ElogE)
10 本章总结
知识点
- 带权图
- 最小生成树问题
- 切分定理
- Kruskal求最小生成树
- Prim求最小生成树
Kruskal和Prim算法的代码实现关键

更多最小生成树的算法