题意描述
马塞尔和瓦勒里乌(Valeriu)所在的疯狂城市由 \(n\) 栋建筑和 \(n\) 条双向道路组成。
马塞尔和瓦勒里乌(Valeriu)分别从 \(a\) 号和 \(b\) 号建筑开始。马塞尔想赶上瓦勒里乌(换句话说,与他在同一栋楼里或在同一条路上相遇)。
在每次移动过程中,他们都会选择前往当前建筑的邻近建筑或留在同一建筑中。由于瓦勒里乌(Valeriu)对马塞尔(Marcel)非常了解,因此瓦勒里乌(Valeriu)可以预测马塞尔(Marcel)下次搬家时会去哪里。瓦勒里乌(Valeriu)可以利用这些信息进行移动。他们同时开始和结束移动。
可以保证任何一对建筑物之间都有路径相连,而且任何一对建筑物之间最多只有一条路。
假设两位棋手都以最优方式下棋,请回答瓦勒里乌(Valeriu)是否有无限期逃离马塞尔(Marcel)的策略。
具体思路
我们知道树是 \(n-1\) 条边的,因此再多加一条边,即 \(n\) 条边的话就会出现环。
设逃离抓捕的人为 \(s\),抓捕的人为 \(t\)。
根据样例 \(1\),我们发现,如果 \(s\) 在环上,那么 \(t\) 将永远无法抓到 \(s\)。
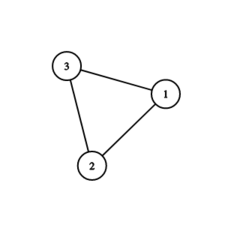
那么思路就很显然了。我们就是要尽量让 \(s\) 快一点跑到环上。这不就是最短路?
当然如果 \(s\) 一开始就在环上,那么就直接输出 YES 就好了。
我一开始的思路是先跑一遍 \(Tarjan\) 求出边双连通分量,即环。然后缩点,比较 \(s\) 和 \(t\) 到环的距离.
设 \(dist(x)\) 表示点 \(x\) 到环的距离。
若 \(dist(s) \ge dist(t)\),那么就是让 \(t\) 先到环上,那么输出 NO。
但是这种思路是有问题的。
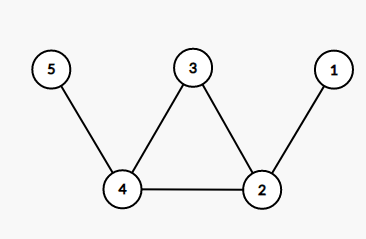
如果 \(s\) 是 \(1\),\(t\) 是 \(5\),那么这两个点到环上的距离都是 \(1\) ,理应输出 NO,但是我们发现,\(s\) 跑到 \(2\) 后,由于他们没有重合,因此 \(t\) 将永远抓不到 \(s\)。
于是思路就变成了对 \(s\) 找到环上最近的点,然后找 \(t\) 到该点的距离,然后比较一下即可。
你可能会问 \(s\) 不会与环上多个点相连吗?显然是不会的,因为你要是和两个点相连,那么就有两个环了,那么总边数就不是 \(n\) 了。
设 \(s\) 到环上最近的点为 \(x\)。
至于找 \(t\) 到 \(x\) 的距离,由于题面的 \(n\) 是 \(2e5\),\(O(Tn\log n)\) 感觉过不去,于是我用 \(dfs\) 的方式来找 \(t\) 到 \(x\) 的距离。这样时间复杂度就是 \(O(Tn)\) 的,感觉可过。
然后就又发现问题了。
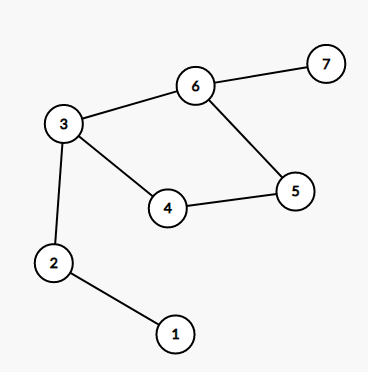
\(s\) 是 \(1\),\(t\) 是 \(7\),那么 \(s\) 到环上最近点 \(x\) 就是 \(3\)。你以为 \(t\) 到 \(3\) 的路径是 \(7-6-3\) 吗?不是!因为你是一个环,所以跑 \(dfs\) 的话有可能路径是 \(7-6-5-4-3\),这个时候你算出来的 \(t\) 到 \(x\) 的距离就会变长,答案也就错了。
因此只能用最短路了。用 spfa 显然是复杂度爆炸,于是采用 dijkstra 来看看能不能水过。最后过啦!
时间复杂度:\(O(Tn \log n)\)。
注意:
样例中有一组 \(s\) 和 \(t\) 重合的样例,直接输出 NO。记得一开始就要判掉。
Code
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
const int N=411000;
struct edge{int x,y,pre;}a[N];
int last[N],alen;
void ins(int x,int y){
a[++alen]=edge{x,y,last[x]};
last[x]=alen;
}
int dfn[N],low[N],id;
int bridge[N];
int cnt,c[N];
void tarjan(int x,int in_edge){
dfn[x]=low[x]=++id;
for(int k=last[x];k;k=a[k].pre){
int y=a[k].y;
if(!dfn[y]){
tarjan(y,k);
low[x]=min(low[x],low[y]);
if(dfn[x]<low[y]){
bridge[k]=bridge[k^1]=1;
}
}
else if(k!=(in_edge^1)){
low[x]=min(low[x],dfn[y]);
}
}
}
int bk;
void dfs(int x,int siz){
c[x]=cnt;
if(siz>1)bk=cnt;
for(int k=last[x];k;k=a[k].pre){
int y=a[k].y;
if(c[y]||bridge[k])continue;
dfs(y,siz+1);
}
}
int v[N];
int dis_st,dis_ed,flag,d;
void dfs_st(int x,int dep){
if(c[x]==bk){
dis_st=dep;
d=x;
flag=1;
return;
}
v[x]=1;
for(int k=last[x];k;k=a[k].pre){
int y=a[k].y;
if(v[y])continue;
dfs_st(y,dep+1);
if(flag)return;
}
}
int dis[N],vis[N];
void dijkstra(int st){
memset(dis,0x3f,sizeof(dis));dis[st]=0;
memset(vis,0,sizeof(vis));vis[st]=1;
priority_queue<PII,vector<PII>,greater<PII>>Q;
Q.push({0,st});
while(!Q.empty()){
int x=Q.top().second;Q.pop();
for(int k=last[x];k;k=a[k].pre){
int y=a[k].y;
if(dis[y]>dis[x]+1){
dis[y]=dis[x]+1;
if(!vis[y]){
vis[y]=1;
Q.push({dis[y],y});
}
}
}
vis[x]=0;
}
}
int main(){
int t;scanf("%d",&t);
while(t--){
int n,st,ed;scanf("%d%d%d",&n,&ed,&st);
alen=1;memset(last,0,sizeof(last));
id=0;
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
dis_st=0,dis_ed=0;
cnt=0;d=0;bk=0;
memset(c,0,sizeof(c));
memset(bridge,0,sizeof(bridge));
for(int i=1;i<=n;i++){
int x,y;scanf("%d%d",&x,&y);
ins(x,y);ins(y,x);
}
if(st==ed){puts("NO");continue;}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i,0);
}
for(int i=1;i<=n;i++){
if(!c[i]){
cnt++;
dfs(i,1);
}
}
memset(v,0,sizeof(v));
flag=0;dfs_st(st,0);
dijkstra(ed);
if(dis_st>=dis[d])puts("NO");
else puts("YES");
}
return 0;
}