评价:无思维场,纯码力场,给我这种无码力选手区分了 -200pts
Fact:因为有补题环节所以打得很激进写了 4 题正解然后开始调 T2,3,4 最后只有 T2,3 过了样例。快结束的时候还给自己都 hack 了。最后喜提暴力分。好处是补题改改就过了()
B - Luogu P4334
省略解法。借这个题讨论一下 e-DCC 和 v-DCC 的联系和区分。有很多定义,下面这个常用:
不存在割边 / 割点的极大连通子图分别定义为 e-DCC 和 v-DCC
基于此容易证明:
Lemma 1: e-DCC 内部任意两点间存在至少两条路径,满足不经过重复边。
Lemma 2: v-DCC 内部任意两点间存在至少两条路径,满足除端点外不经过重复点。
观察到性质 2 严格于 1,因此点双连通图一定是边双连通图(不一定是分量,因为更严格的约束可能导致不满足极大性)。考虑下面的图
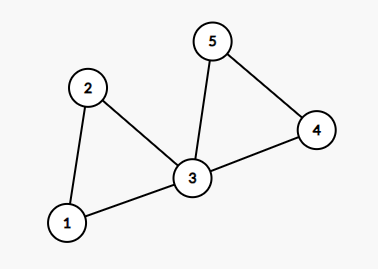
存在两个 v-DCC,一个 e-DCC。
因此我们发现解决无向图连通性问题更通用的方法是基于点双:圆方树。实际上割边也一定出现在圆方树上,以一个大小为 \(2\) 的 v-DCC(一个度数为 \(2\) 的方点)形式存在。
所以这个题我们只需要建立一棵圆方树,不需要再进行 e-DCC 缩点。
C - Luogu P5786
注意到若每个点都有出度,因为这个图是 DAG 且只有一个点出度为 \(0\),所以一定能在反图拓扑序上遍历到所有点,也就是满足题目要求。
所以不用管原图形态,只要每个点都有出度就行了。在此基础上最小化入度最多的节点入度(根除外)。
二分答案之后的判定问题涉及到 出入度问题,想都不用想直接拆点二分图网络流(?
然后这个题更难的其实是字典序最小的要求。因为网络流上直接贪心是保证不了这个性质的,因为有反悔操作。
但是 \(n\le 50\),所以我们在得到 \(ans\) 后,整个流图固定下来。直接在 外层贪心,设贪心到 \(i\),前面的字典序最小的父亲已经固定了,枚举 \(i\) 的父亲也固定下来。这些固定操作,只需要不建出 \([1,i]\) 的出边,然后减少其父亲的剩余容量,对 \([i,n]\) 出发的点正常跑网络流判定。
从小到大枚举父亲,可行后直接跳到下一个 \(i\)。
但是上面那是一个即便在二分图上也跑到了 \(O(n^2m\sqrt{n})=O(n^{4.5})\) 的做法不是很好。还可以优化很多。
实际上不需要二分,因为 \(n\) 比较小。
那么我们就可以依次加边跑网络流,这部分少了一个 \(\log\)。
输出方案部分,观察到操作相当于依次删边或者减少容量(也等价于删边)。退流即可。
D
假设字符集大小为 \(4\)。给定 \(n\) 个字符串二元组 \((a_i,b_i)\),满足 \(|a_i|=|b_i|\)。定义对长度为 \(k\) 的字符串 \(S\) 的操作为:交换相邻元素;或者若 \(\exists i\),满足 \(S\) 有子串 \(b_i\),则可以将这个子串换成 \(c_i\)。求最少所需颜色数,使得对所有 \(4^k\) 个可能的 \(S\) 染色,任意 \(S\) 任意次操作后不能达到与其同色的任何串。
观察到任意次交换相邻元素等价于任意重排序列。因此只关心 \(4\) 种字符各自的出现次数。
这样的 \((a,b,c,d)\) 状态数很少,只有不到 \(10^4\)。一个状态内部的所有 \(\binom{k}{a}\binom{k-a}{b}\binom{k-a-b}{c}\) 种串必须分别赋予不同的颜色。
然后直接联想到图论问题。根据第二种操作连边,缩点。一个 SCC 内部的颜色数是所有其中状态的颜色数求和,设为这个点的权值。
进而在一个 DAG 上跑,有一个结论:答案为该 DAG 上带权最长路长度。
直接证明很困难,因为路径可以在多处相交。考虑数学归纳法:按照拓扑序依次考虑每个 \(x\),假设只考虑能到达 \([1,x]\) 的点构成的子图满足结论。
那么对于新的点,其入边对应端点若互相不可到达,则显然正确;否则设 \(y\) 可以到达 \(z\),则 \(ans_z\ge ans_y\) ,因为可到达其的子图包含了 \(x\) 的对应子图。因此我们直接舍弃 \(y\)。