526互联

题解 P3225 [HNOI2012] 矿场搭建

发布时间 2023-04-28 21:16:22作者: cmd_pig

解析

传送门

一道简单的tarjan题

题意：在无向图中找一些点，这些点组成的的点集记为\(V\) ，使得去掉任意一个点，剩下的每一个点都可以到达\(V\)中任意一个点，求点集\(V\)的大小的最小值及其方案数。

去掉一个点，很自然的联想到割点，那么考虑一下割点在不在备选集合中。

1234

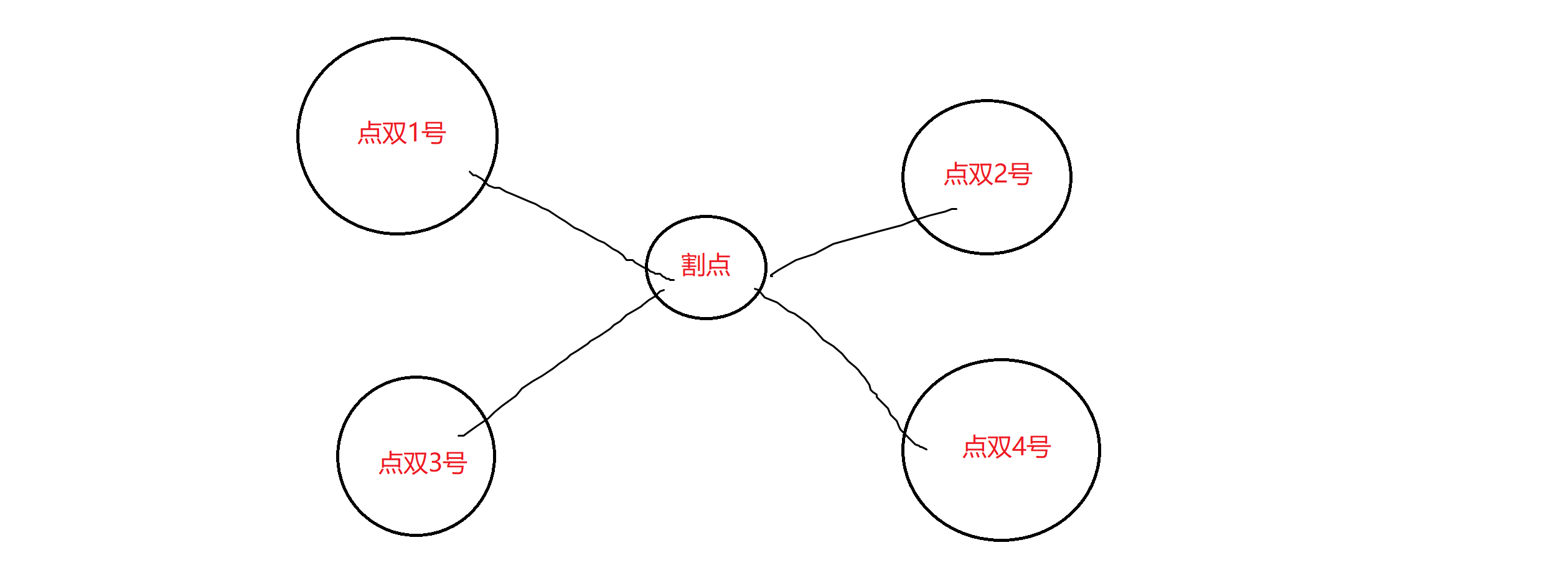
如图，显然可以看出，在割点上设立出口是劣的，因此我们永远不会在割点上设立出口。

既然不在割点上设立出口，那我们就把目光投向点双。

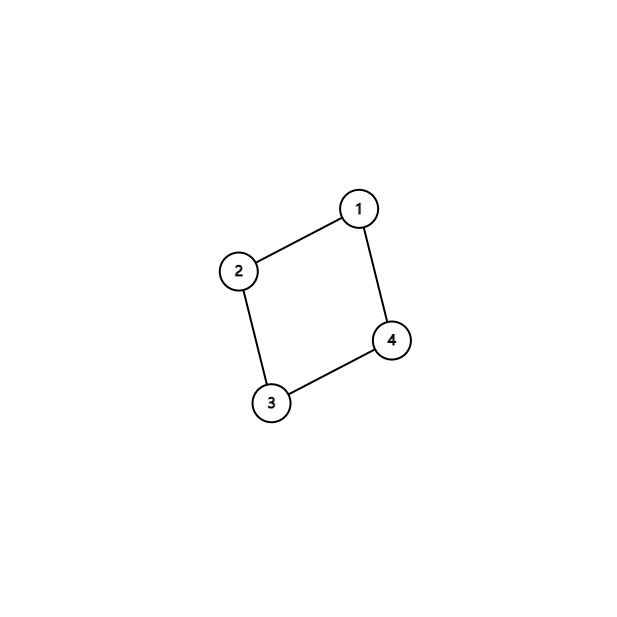
graph (3)

根据点双的定义，无论我们去掉哪一个点，剩下的点都可以相互到达。

因此我们只要在一个点双内设立两个出口就可以保证题目要求，方案数为\(\tbinom{n}{2}\)（证明很简单，分类讨论即可）

注意：刚才我们讨论的是一个点双，现在范围扩大一下

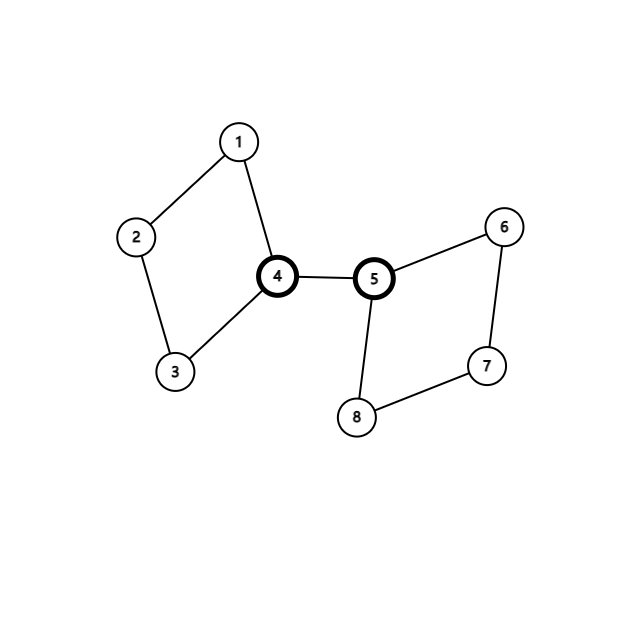
graph (4)

现在两个点双各被一个割点（加粗的黑点）相连了，每个点双内需要设立的出口数就变成了一个，Why？

  1. 假如去掉的点是割点

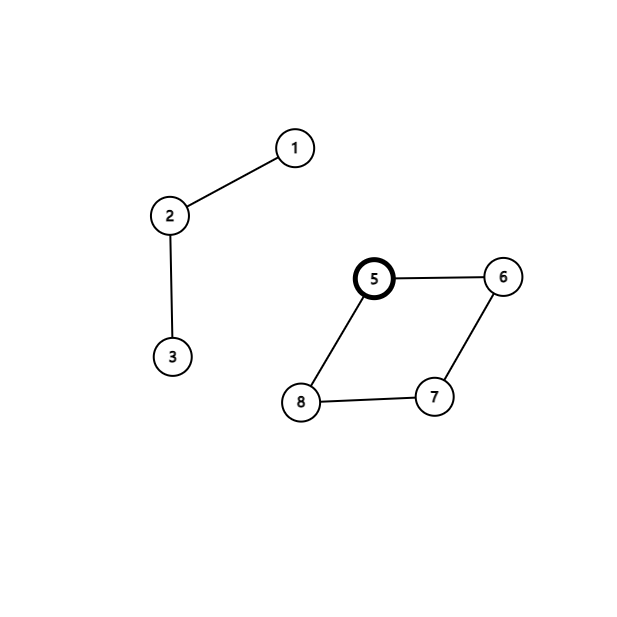
    graph (5)

    根据点双的定义，每个点双内部的点都能到达自己的出口。

  2. 假如去掉的点是点双内部的一个出口（这里假设为\(2\)）

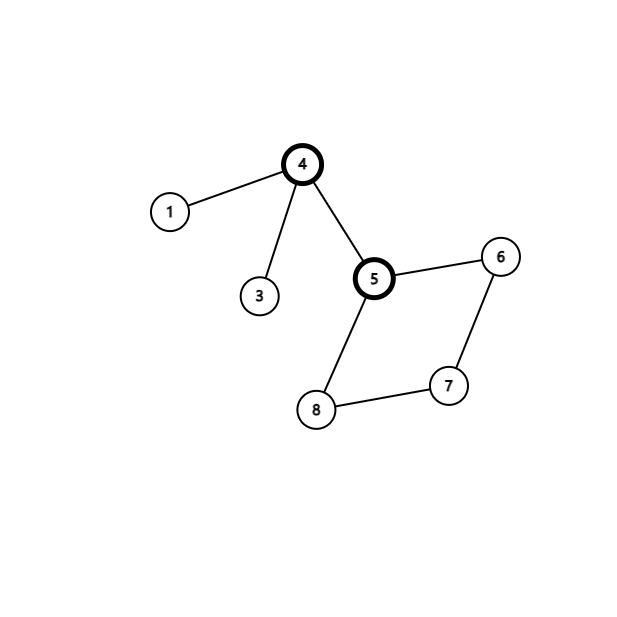
    graph (6)

    虽然\(1\)，\(3\)到达不了\(2\)，但它们可以借助割点组成的“桥”来到达其他点。（这里的桥仅作比喻用）

如此，便可以得出：一个点双与一个割点相连只要设立一个出口，方案数为\(n\)

一个点双与两个及以上割点相连的情形是简单的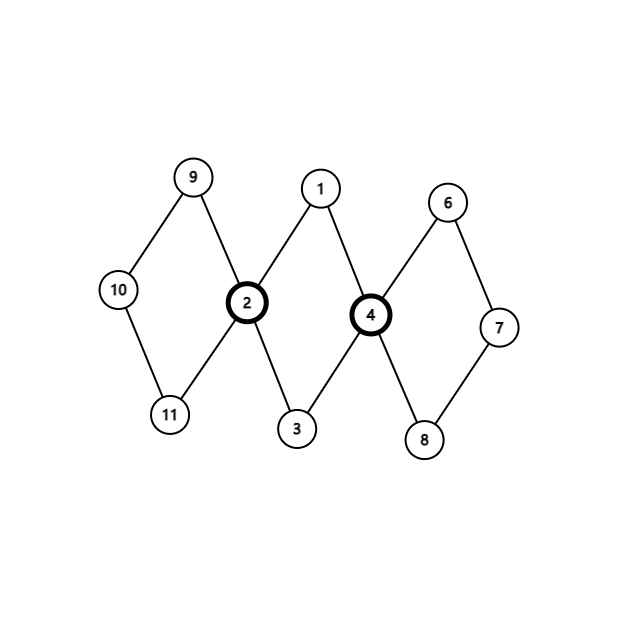graph (7)

点集\(\{1,2,3,4\}\)组成的点双与两个割点相连，这意味着无论断哪个割点，这个点双内的剩余点都可以沿着其他割点走到别的点双内的出口。

有人一定要说：那我每个点双都与两个割点不就好了吗？

答案显然是不行

在只保留割点的情况下，所有的割点构成一棵无根树

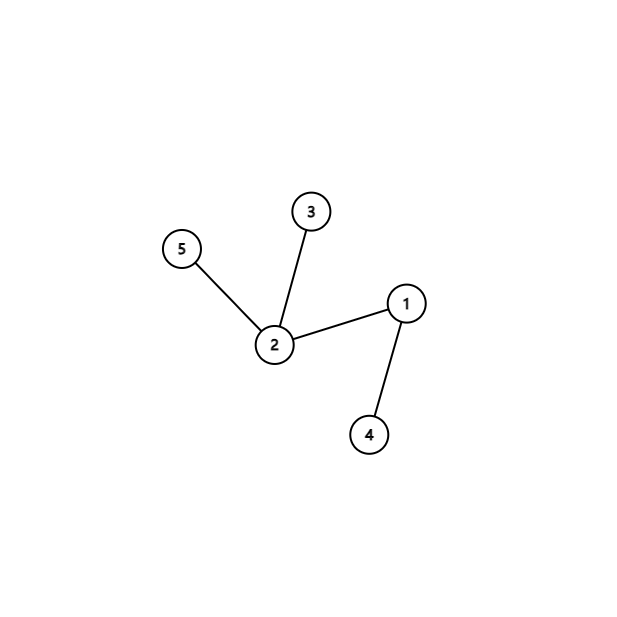
graph (8)

根据割点的定义，每个割点都至少与一个点双相连

考虑度为\(1\)的节点

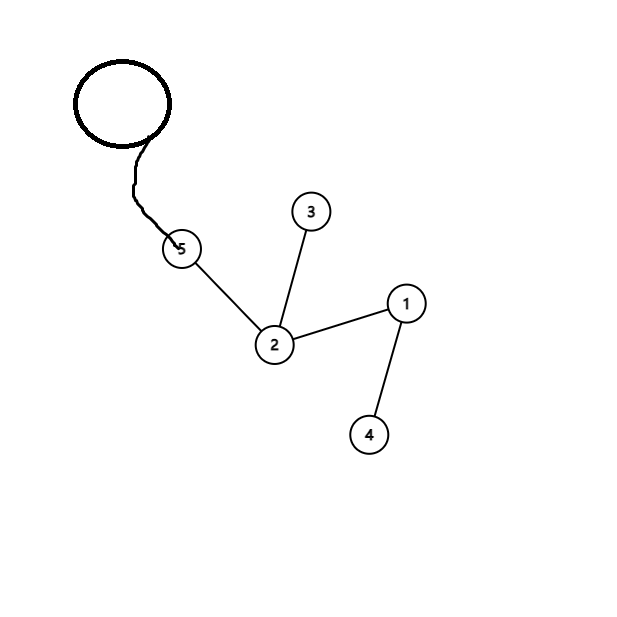
12345

这个黑色圆圈代表的点双只要再连任意一条道割点的边，就会形成一个环，而这与割点的定义不符。

由此便可以写代码了，方案数按照乘法原理一个一个一个相乘就好了

代码

总算说完又臭又长的解析了，如果很急的话直接看代码就好了

注意割点不能选，算点双大小时不能把割点带上

code 
// Problem: P3225 [HNOI2012]矿场搭建
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3225
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define db double 
using namespace std;
const ll INF=1e18+7;
const db eps=1e-9;
const int MAXN=1e3+3;
ll n,m;
ll ans,ANS;
ll CNT,low[MAXN],dfn[MAXN],cnt;
vector<ll> graph[MAXN];
ll T,cut[MAXN],flag[MAXN],size,CUT;
void tarjan(int u,int fa){
	low[u]=dfn[u]=++cnt;
	int child=0;
	for(auto v:graph[u]){
		if(v==fa) continue;
		if(!dfn[v]){
			child++;
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u]&&fa!=u){
				cut[u]=1;
			}
		}
		else{
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(u==fa&&child>=2){
		cut[u]=1;
	}
}

void clear(){
	ans=1,ANS=CNT=cnt=0;
	for(int i=1;i<=n;i++){
		graph[i].clear();
	}
	memset(dfn,0,sizeof(dfn));	
	memset(low,0,sizeof(low));
	memset(flag,0,sizeof(flag));
	memset(cut,0,sizeof(cut));
}
void dfs(int u){
	flag[u]=CNT;
	size++;
	for(auto v:graph[u]){
		if(flag[v]!=CNT&&cut[v]==1){
			CUT++;
			flag[v]=CNT;
		}
		if(flag[v]==0){
			dfs(v);
		}
	}
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    while(1){
    	clear();
    	T++;
    	cin>>m;
    	if(m==0){
    		break;
    	}
    	n=0;
    	for(int i=1;i<=m;i++){
    		ll u,v;
    		cin>>u>>v;
    		graph[u].push_back(v);
    		graph[v].push_back(u);
    		n=max(n,max(u,v));
    	}
    	for(int i=1;i<=n;i++){
    		if(!dfn[i]){
    			tarjan(i,i);
    		}
    	}
    	for(int i=1;i<=n;i++){
    		if(!cut[i]&&!flag[i]){
    			size=CUT=0;
    			CNT++;
    			dfs(i);
    			if(CUT==0){
    				ANS+=2;
    				ans*=size*(size-1LL)/2LL;
    			}
    			if(CUT==1){
    				ANS+=1;
    				ans*=size;
    			}
    		}
    	}
    	cout<<"Case "<<T<<": "<<ANS<<" "<<ans<<"\n";
    }
    return 0;
}