[CF762D] Maximum path 题解

想法

首先考虑问题的弱化版，如果不能往左走，能取到的最大值是多少。

这个问题可以用一个显然的 DP 解决，\(f_{i,j}\) 表示走到第 \(i\) 列，第 \(j\) 行，并且不会再访问这一列其它的方格，能取到的最大值。

转移可以从三个方向考虑，以 \(f_{i,1}\) 为例，黑色是当前状态，红黄蓝是可能的三个转移方向，每一个状态可以取到箭头经过的点的权值。\(f_{i,2}, f_{i,3}\) 同理。

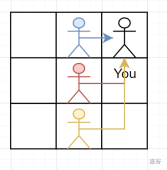
思路

但是原题中人是可以往左回头走的，这样这个单纯的转移就不成立了，因为回头走会出现后效性。

既然如此，可以想一下有没有什么性质尚未被观察到。

根据人类的直觉，小人应该是不会回头走太多步的，这个直觉是正确的，小人最多回头走 \(1\) 格。

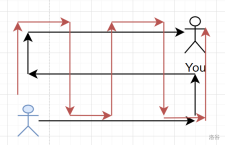
如图，黑色的路径和红色路径得到的权值是相等的。

猜测 所有的回头路径都有一个修正的路径对应。

回头走的真谛是在遍历蓝色小人到黑色小人每一行的格子，如果能找到一条最多回头一次的路径也能遍历这些格子，就可以证明上面的引理。

观察到这种走法可以让要遍历的格子列数减去 2，而行位置不变。

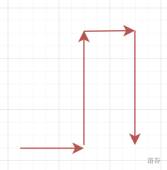
那么如果要遍历的列数是奇数，可以直接一直走上图走法，剩余遍历列数是 1 时，直接往上走到目标点。

如果列数是偶数，则在剩余遍历列数是 2 时，走一次下图走法，回头一次走到目标点：

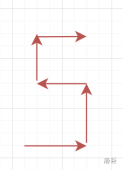
所以证明了对于任意一个最优解，都有一个最多只需要回头一次的路径得到的权值与其相等。

所以这样就好做了，我们只需要在弱化版的 DP 转移里面加上回头一次的情况。

\(f_{i, 2}\) 的转移不会出现回头的情况，而 \(f_{i,1}, f_{i, 3}\) 加上回头转移的即可，以 \(f_{i, 1}\) 为例，转移绿色路径：

问题得到了解决。

代码实现

时间复杂度：\(O(n)\)。

// Problem: Maximum path
// Author: Moyou
// Copyright (c) 2023 Moyou All rights reserved.
// Date: 2023-09-29 19:36:59

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
long long a[3][N], f[N][3];

signed main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    for(int i = 0; i < 3; i ++) {
        for(int j = 1; j <= n; j ++) {
            cin >> a[i][j];
        }
    }
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for(int i = 1; i <= n; i ++) {
        long long sum = 0;
        for(int j = 0; j < 3; j ++) {
            sum += a[j][i] + a[j][i - 1];
        }
        f[i][1] = max({f[i - 1][0] + a[0][i], f[i - 1][1], f[i - 1][2] + a[2][i]}) + a[1][i];
        f[i][0] = max({f[i - 1][0], f[i - 1][1] + a[1][i], f[i - 1][2] + a[2][i] + a[1][i]}) + a[0][i];
        f[i][2] = max({f[i - 1][2], f[i - 1][1] + a[1][i], f[i - 1][0] + a[0][i] + a[1][i]}) + a[2][i];
        if(i > 1) {
            f[i][0] = max(f[i][0], f[i - 2][2] + sum);
            f[i][2] = max(f[i][2], f[i - 2][0] + sum);
        }
    }
    cout << f[n][2] << '\n';
    return 0;
}