题意
给定两个森林 \(A\) 和 \(B\),均有编号 \(1\) 到 \(n\) 的节点,边数分别为 \(m_1,m_2\)。
现在进行加边操作,但是有两个要求:
- 如果在第一个森林加一条 \((u,v)\) 的边,第二个森林也要进行同样的操作。反之同理。
- 加边后两个森林依旧是森林。一棵树也是森林。
求最多能加几条边,并输出加边方案。若有多解,输出任意一种。
\(1\le n\le10^5\)。\(0\le m_1,m_2<n\)。
思路
“加边后森林依旧是森林” 的意思是,若 \((u,v)\) 已经连通,则不能加边,否则就成环了。
首先有一个暴力的做法:用并查集维护连通性,枚举所有点对 \((u,v)\),如果 \((u,v)\) 在 \(A\) 和 \(B\) 中都不连通,则加边。
这样做为什么是对的呢?我们将连通块看成一个整体,那么连边就相当于在连通块之间加边。那么,每连一条边,两个图中都会少一个连通块。并且,可以证明两个森林到最后一定会至少有一个是树(证明见下)。因此一直这样连就可以了。
证明:假设现在已经不能连边。不妨设 \(A\) 存在两个或多个连通块,那么所有在 \(A\) 中不连通的点对 \((u,v)\),一定在 \(B\) 中连通。
因此,对于 \(A\) 中的一个连通块 \(C\),对于所有 \(u\in C,v\notin C\),有 \((u,v)\) 在 \(B\) 中连通。 由此也可知 \(C\) 中的点在 \(B\) 中两两连通,不在 \(C\) 中的点在 \(B\) 中两两连通。所以所有点在 \(B\) 中两两连通,即 \(B\) 是一棵树。
平均时间复杂度 \(O(n^2\alpha(n))\),无法通过。
考虑如何优化这个贪心。
我们确定一个中心点 \(s=1\)。
考虑一个点 \(x\) 有多少种状态:
- \(x\) 与 \(s\) 在 \(A\) 中连通,在 \(B\) 中连通;
- \(x\) 与 \(s\) 在 \(A\) 中连通,在 \(B\) 中不连通;
- \(x\) 与 \(s\) 在 \(A\) 中不连通,在 \(B\) 中连通;
- \(x\) 与 \(s\) 在 \(A\) 中不连通,在 \(B\) 中不连通。
首先,枚举所有 \(x\),如果 \(x\) 为状态 4,则 \(x\) 与 \(s\) 间连一条边。
然后我们考虑还有哪些点之间能连边。状态 1 肯定不能连边,考虑状态 2 和 3。
我们仍然把连通块看成整体。如下图:(方点代表连通块,数字代表状态)(当然实际情况很可能不是这样)
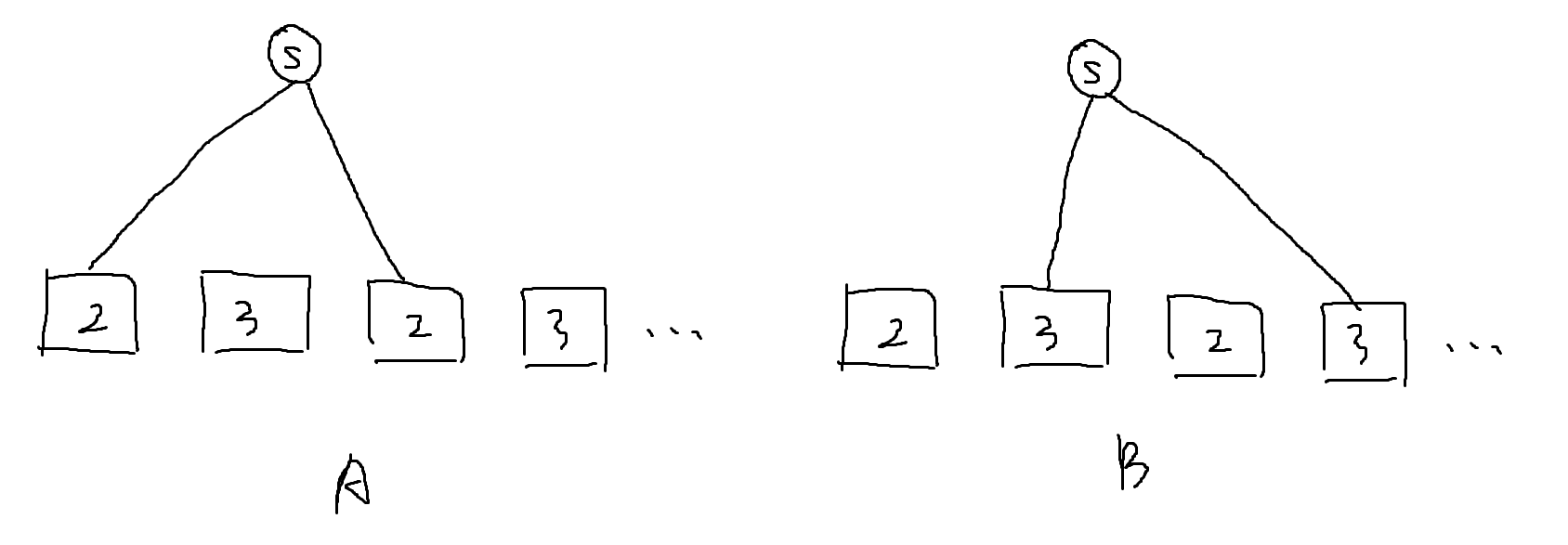
我们发现可以这样连边:
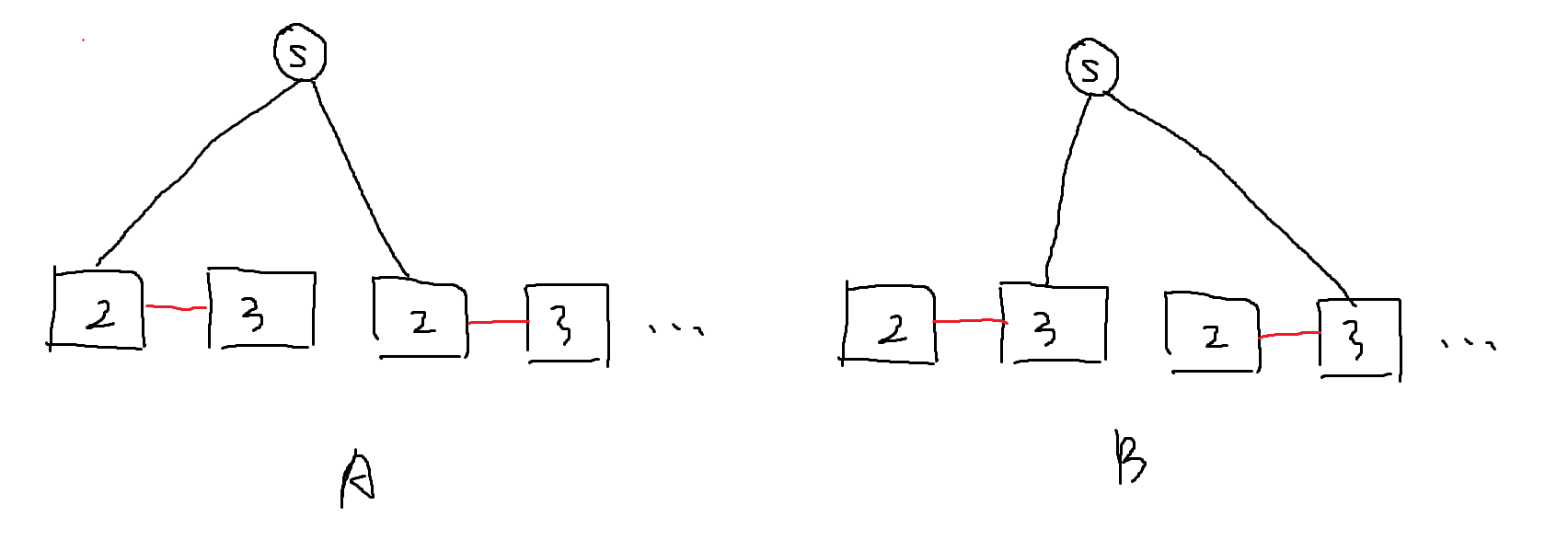
因此,记录所有状态为 2 和 3 的连通块(具体实现见代码),然后尽量一对一连边。
最坏时间复杂度 \(O(n\log n)\),可以通过。
代码
#include <vector>
#include <iostream>
#define f(x, y, z) for (int x = (y); x <= (z); ++x)
using namespace std;
typedef pair<int, int> pii;
int constexpr N = 1e5 + 10;
int n, m[2], u, v;
int fa[2][N];
int getfa(int x, int f) { return x == fa[f][x] ? x : fa[f][x] = getfa(fa[f][x], f); }
void unionn(int x, int y,int f) { fa[f][getfa(x, f)] = getfa(y, f); }
vector<pii> ans;
vector<int> vec[2];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m[0] >> m[1];
f(i, 1, n) fa[0][i] = fa[1][i] = i;
f(j, 0, 1) f(i, 1, m[j]) {
cin >> u >> v;
if (getfa(u, j) ^ getfa(v, j)) unionn(u, v, j);
}
f(i, 2, n) if ((getfa(1, 0) ^ getfa(i, 0)) && (getfa(1, 1) ^ getfa(i, 1))) //状态 4
ans.emplace_back(1, i), unionn(1, i, 0), unionn(1, i, 1);
f(i, 2, n) f(j, 0, 1) if (getfa(1, j) ^ getfa(i, j)) //状态 2 和 3
vec[j].push_back(i), unionn(1, i, j); //记录的同时 unionn, 则这个连通块其他点不会再被记录
if (vec[0].size() > vec[1].size()) swap(vec[0], vec[1]);
cout << ans.size() + vec[0].size() << '\n';
for (auto [u, v]: ans) cout << u << ' ' << v << '\n'; //c++17
for (int i = 0; i < (int)vec[0].size(); ++i)
cout << vec[0][i] << ' ' << vec[1][i] << '\n';
return 0;
}