编译原理 | Concepts & Review-526互联

怎么感觉像是在学算法(

本文主要从词法分析, 语法分析, 语义分析三个章节总结.

1 词法分析

首先, 应该知道编译器的流程是词法分析 -> 语法分析 -> 语义分析 -> 中间代码生成 -> 代码优化 -> 目标代码生成. 旁边还有一个符号表.

词法分析分解源程序, 输出单词序列 (关键字, 标识符, 运算符等).
语法分析根据单词序列, 输出语法树 (AST). 注意语法树和分析树完全不是一个概念.
语义分析检查程序有无语义错误, 输出注释语法树.
中间代码生成将语法树变为内部表示形式, 输出三地址代码.
代码优化节省时间和空间, 输出优化后的中间代码.
目标代码生成转化为指令代码, 输出可执行的机器码.

1.1 正规式

举一些例子:

\d 或 [0-9] 匹配任意数字.
hello 仅匹配字符串 hello.
[a-zA-Z] 匹配任意英文字母.
a* 匹配零个或多个 a.
(a|b)*c 匹配以 c 结尾, 前面有任意多个 a 或 b 的字符串.
(00|11)*((01|10)(00|11)*(01|10)(00|11)*)* 匹配偶数个 0 和偶数个 1 的正规式.

为什么呢? 看下面这张状态转换图.

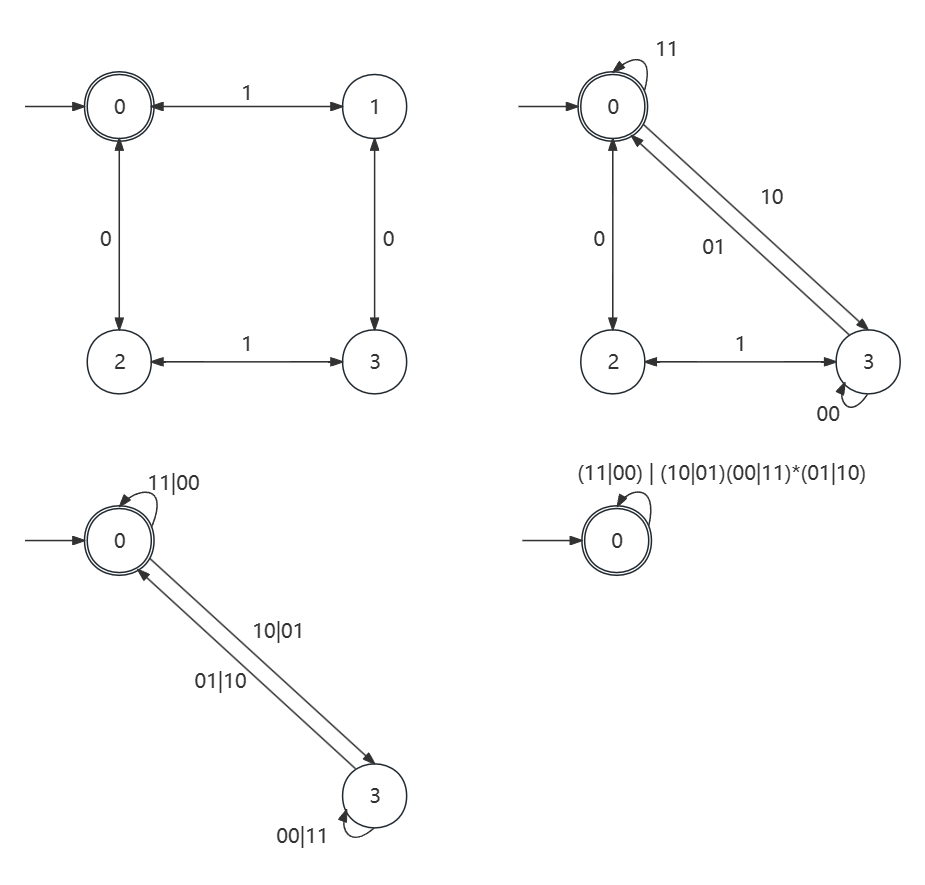
注意到 a*(ba*)*=(a|b)* 是恒成立的, 那么 (00|11)*((01|10)(00|11)*(01|10)(00|11)*)*=((11|00)|(10|01)(00|11)*(01|10))*.

1.2 有限自动机

让我们来画出正规式 (a|b)*ab 的 DFA.

第一步 画出 NFA.

规则有三个:

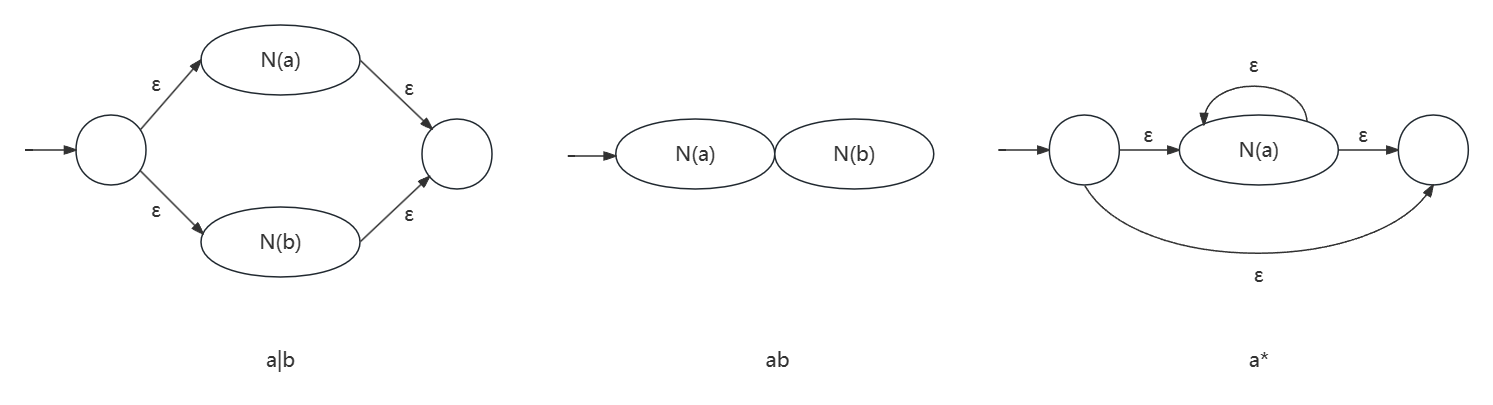
因此 (a|b)*ab 的 NFA 是

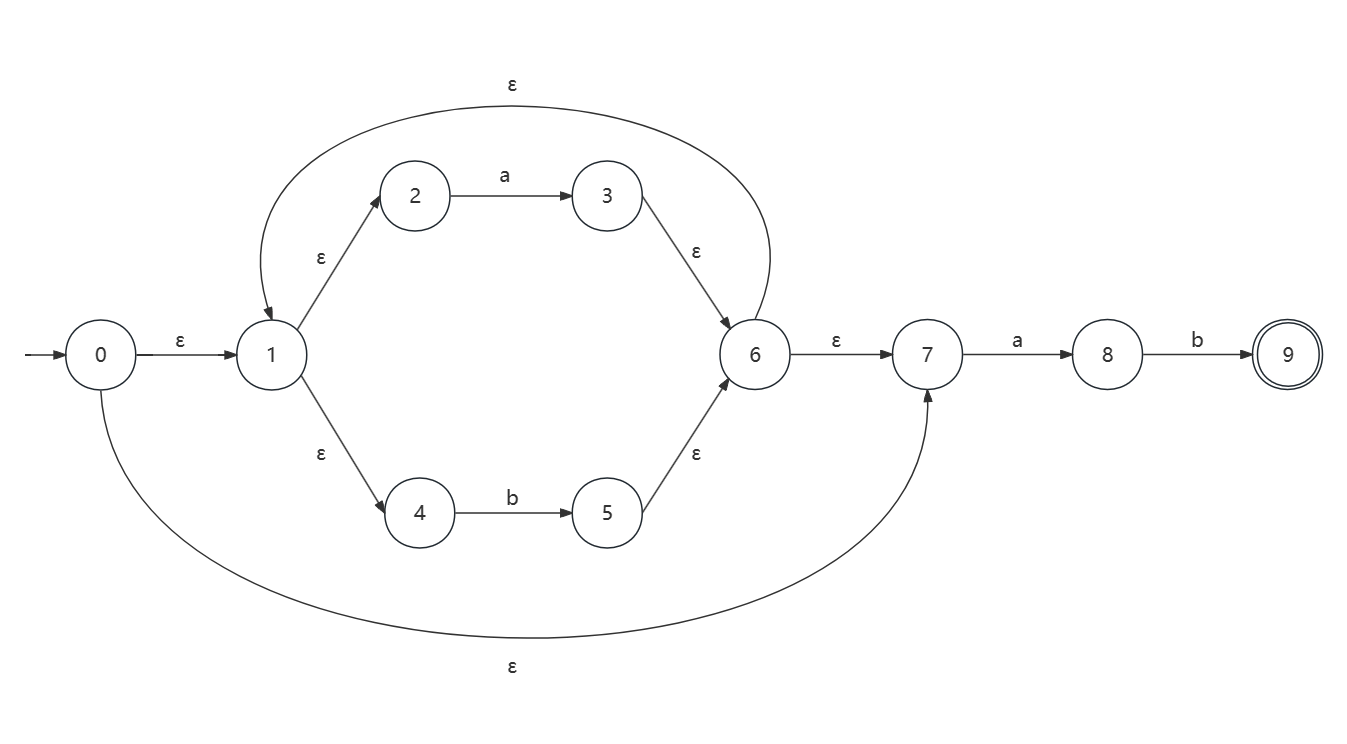
第二步 将 NFA 转变为 DFA.

这里采用子集构造法.

首先从状态 0 开始, 找出用 ε 连接的其他状态, 这些状态组成了一个集合 A = {0, 1, 2, 4, 7}. 子集构造法的思想正是把一个集合内的元素看成是一个状态.

集合 A 在接受 a 后, 得到集合 B = {1, 2, 3, 4, 6, 7, 8}; 集合 A 在接受 b 后, 得到集合 C = {1, 2, 4, 5, 6, 7}. 这样集合 A 就处理完了.
集合 B 在接受 a 后仍然是 B; 集合 B 在接受 b 后, 得到集合 D = {1, 2, 4, 5, 6, 7, 9}. 这样集合 B 就处理完了.
集合 C 在接受 a 后得到 B; 集合 C 在接受 b 后仍然是 C. 这样集合 C 就处理完了.
集合 D 在接受 a 后得到 B; 集合 D 在接受 b 后得到 C. 这样集合 C 就处理完了.

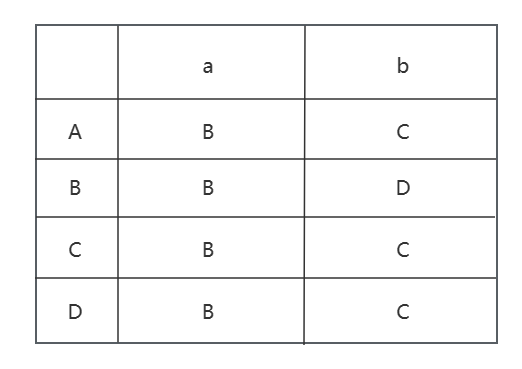
第三步 将 DFA 化为最简形式.

化简的本质是合并表面看上去一样的状态, 比如上图中 A 接受 a 到达 B, 接受 b 到达 C; C 接受 a 同样到达 B, 接受 b 同样返回 C.

对于一个 DFA, 如果出现了一个状态, 它仅仅接受一部分输入符号, 那么称这个 DFA 的转换函数不是全函数. 此时额外添加一个 "死状态", 死状态接受所有输入符号并回到自身, 这样原本的 DFA 就实现全函数了.

除了目测化简外, 标准的算法是将所有状态分为两类: 接受状态子集和非接受状态子集. 对上图 DFA 而言, 它们分别是 {D}, {A, B, C}.

接下来考察 {A, B, C}: A(a) -> B, B(a) -> B, C(a) -> B; A(b) -> C, B(b) -> D, C(b) -> C.

注意到 A 和 C 接受 a 或 b 仍然处于子集 {A, B, C}, 只有 B 接受 b 转换到了子集 {D}. 那么将 {A, B, C} 划分为 {A, C} 和 {B}, {B} 和 {D} 合并得到新的接受状态子集 {B, D}.

接下来考察 {A, C}: A(a) -> B, C(a) -> B; A(b) -> C, C(b) -> C.

注意到 A 和 C 接受 a 都转换到了子集 {B, D}, 接受 b 都仍处于子集 {A, C}. 这说明 A 和 C 没有办法区分了, 选择 A 作为 {A, C} 的代表.

这样我们成功画出了正规式 (a|b)*ab 的最简 DFA.

2 语法分析

语法分析分为自上而下和自下而上两种. 后者通常比前者强大.

2.1 各种形式语言

文法的表示方式是 $G = (V_T, V_N, S, P)$, $V_T$ 是终结符 (Terminal), $V_N$ 是非终结符 (Non-terminal), $S$ 是起始符号 (Start), $P$ 是产生式 (Production).

Chomsky 把文法分成了四种类型: 0 型, 1 型, 2 型, 3 型.

0 型文法称为短语文法, 定义为对于每个产生式 $\alpha\rightarrow\beta$ 都满足 $\alpha,\beta\in(V_N\cup V_T)^*$, 每个产生式的 $\alpha$ 都至少含有一个非终结符.

可以生成任何可计算的语言.

1 型文法称为上下文有关文法, 在短语文法的基础上, 还满足每一个产生式的右侧长度不小于左侧长度.

每个产生式都可以写成 $\alpha A\beta\rightarrow \alpha\gamma\beta$ 的形式, 非终结符 $A$ 只有在 $\alpha$ 和 $\beta$ 这样的环境 (上下文) 中才能替换为 $\gamma$.

2 型文法称为上下文无关文法, 在短语文法的基础上, 还满足每一个产生式都是 $A \rightarrow \beta$ 的形式, 其中 $A\in V_N$.

每个产生式的左侧只有一个非终结符, 这个非终结符的替换不依赖于它周围的符号 (上下文).

3 型文法称为正规文法, 在短语文法的基础上, 还满足每一个产生式都是 $A\rightarrow aB$ 或 $A\rightarrow a$ 的形式, 其中 $A,B\in V_N$, $a\in V_T$.

可以由正规式完全描述, 是最基本的语言类型.

举一些例子:

$AB\rightarrow a$ 是一个短语文法的产生式; $aAbB\rightarrow abAB$ 是一个上下文有关文法的产生式; $A\rightarrow aBb$ 是一个上下文无关文法的产生式; $A\rightarrow aB$ 是一个正规文法的产生式.

接下来使用的基本都是上下文无关文法. 因为最有效的语法分析方法只能处理上下文无关文法的子类.

2.2 消除二义性, 左递归, 左因子

如果一个文法没有二义性, 那么它无论是最左还是最右推导必然得到同一个分析树, 只不过是叶节点从左向右还是从右向左生成的区别.

二义性的典例是悬空 else 问题: stmt -> if expr then stmt | if expr then stmt else stmt | other.

如果输入 if expr then if expr then stmt else stmt

到底是

\[\begin{aligned} &\text{if expr}\\\\ & \quad\quad \text{if expr}\\\\ &\quad\quad\quad\quad \text{stmt}\\\\ &\quad\quad \text{else}\\\\ &\quad\quad \quad\quad \text{stmt} \end{aligned} \]

还是

\[\begin{aligned} &\text{if expr}\\\\ &\quad\quad \text{if expr}\\\\ &\quad\quad\quad\quad \text{stmt}\\\\ &\text{else}\\\\ &\quad\quad \text{stmt} \end{aligned} \]

呢?

根据就近原则, 选择第一种.

自上而下的方法不能出现形如 $A\rightarrow A\alpha$ 形式的左递归.

为什么呢?

A 会不停地推出以 A 起始的串, 无限循环, 换句话说你永远得不到 A 的 FIRST 集.

对于直接左递归, 将 $A\rightarrow A\alpha|\beta$ 改写为 $A\rightarrow \beta A'$ 和 $A'\rightarrow \alpha A'|\varepsilon$.

对于间接左递归, 将所有非终结符按一定顺序排列, 用两层 for 将每一对 $A_i\rightarrow A_j \beta$ 转变为 $A_i\rightarrow \alpha_1 \beta|\alpha_2 \beta|\cdots| \alpha_k \beta$ 的形式, 如果其中存在左递归则消除. 最后删除与文法开始符号不相关的产生式.

自上而下的方法不能出现形如 $A\rightarrow \alpha\beta_1 | \alpha\beta_2$ 形式的左因子.

为什么呢?

输入一行 $\alpha$ 起始的串时, 分析树不知道往两个选项中哪一个去构建, 也就是歧义.

提取左因子可以消除这个问题, 即改写成 $A\rightarrow \alpha A'$ 和 $A'\rightarrow \beta_1|\beta_2$. 其中 $\beta_1$ 和 $\beta_2$ 已经是终结符了, 不会再有歧义.

2.3 自上而下的 LL(1) 文法与分析表

对于一个输入串, 每输入一个符号, 建立的分析树就生长一点, 但是构建分析树时不能盲目试错 (产生回溯).

比如文法 S->aCb, C->cd|c 对于输入串 acb 和输入指针 ->c, 会出现 C->cd 和 C->c 两种可能, 这两种都符合指针指向的符号 c, 产生了歧义.

LL(1) 文法是一种特殊的自上而下方法, 定义是对于任意产生式 $A\rightarrow \alpha|\beta$, 满足:

$FIRST(\alpha)\cap FIRST(\beta)=\emptyset$

这保证了两个子选项 $\alpha,\beta$ 无歧义.

若 $\beta\Rightarrow ^*\varepsilon$, 则 $FIRST(\alpha)\cap FOLLOW(A)=\emptyset$

如果 $\beta$ 能推出空字符串, 分析器在处理 $A$ 时可能会看到紧跟其后的符号, $\alpha$ 不能和紧跟其后的符号产生歧义.

LL(1) 第一个 L 指的是从左向右扫描输入, 第二个 L 指的是最左推导, (1) 指的是每步动作向前查看的符号个数为 1. 可以证明, LL(1) 文法不是二义的, 无左因子, 也没有左递归.

在构建 LL(1) 的分析表前, 定义 FIRST 和 FOLLOW 集合如下:

FIRST 集合为一个非终结符能推出的串的第一个终结符的集合. FOLLOW 集合为一个非终结符后面紧跟的终结符的集合. 文法的开始符号的 FOLLOW 集中必定含有 $ 符号.

怎样手工画 LL(1) 分析表呢?

对每个产生式 $A\rightarrow\alpha$, 执行:

将 $FIRST(\alpha)$ 加入分析表.
如果 $FIRST(\alpha)$ 包含空串 $\varepsilon$, 将 $FOLLOW(\alpha)$ 加入分析表.

让我们来画出文法 E->TE', E'->+TE'|ε, T->FT', T'->*FT'|ε, F->(E)|id 的分析表.

第一步 确定所有的 FIRST 和 FOLLOW 集合.

FIRST(E) = FIRST(T) = FIRST(F) ={(, id}.

FIRST(E') = {+, ε}.

FIRST(T') = {*, ε}.

FOLLOW(E) = FOLLOW(E') = {), $}.

FOLLOW(T) = FOLLOW(T') = {+, ), $}.

FOLLOW(F) = {+, *, ), $}.

第二步 建立分析表.

LL(1) 的分析表应该长这样:

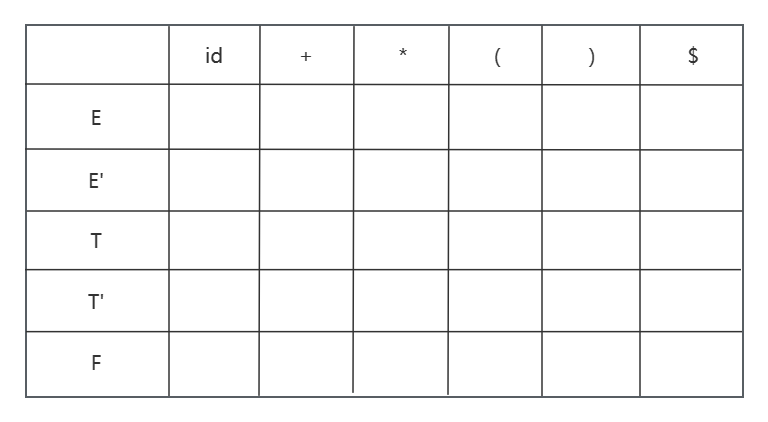
考察第一个产生式 E->TE', 因为 FIRST(TE') = FIRST(T) = {(, id}, 那么将 E->TE' 写入分析表中, 得到:

这意味着分析树建立到非终结符 E 的时候, 输入符号只有是 'id' 或 '(' 才是合理的, 分析树按照 E->TE' 继续生长.

考察第二个产生式 E'->+TE'|ε, 因为 FIRST(+TE') = {+}, 那么将 E'->+TE' 写入分析表中; 因为 E' 能推出空串 ε, 那么将 E'->ε 写入分析表中, 得到:

考察第三个产生式 T->FT', 因为 FIRST(FT') = FIRST(F) = {(, id}, 那么将 T->FT' 写入分析表中, 得到:

考察第四个产生式 T'->*FT'|ε, 因为 FIRST(FT') = {}, 那么将 T'->*FT' 写入分析表中; 因为 T' 能推出空串 ε, 那么将 T'->ε 写入分析表中, 得到:

考察第五个产生式 F->(E)|id, 因为 FIRST((E)) = {(}, FIRST(id) = {id}, 那么将 F->(E)|id 写入分析表中, 得到:

第三步 添加错误恢复.

在建立好的分析表中, 对所有剩下的 FOLLOW 集中元素添加 synch. 意思是某一个非终结符 (非终结符代表的就是一个代码块或称函数) 出错, 但是其后紧跟的符号 (其他代码块或函数) 仍然是可以执行的.

分析表中会出现两种错误: 空白错误 (跳过当前输入符号) 和 synch 错误 (无须跳过).

以上是完整的 LL(1) 分析表构建过程. 自上而下的文法分析至此结束.

2.4 自下而上的 SLR, LR, LALR 文法与分析表

每读入一个输入符号称为移进.

归约是产生式的逆过程, 对于人来说相当于自上而下采用最右推导, 对于机器来说相当于自下而上采用最左归约.

当然你也可以把归约理解成: 删去原本的终结符, 用一个非终结符替换, 得到一个新的输入串. 原本的终结符就像什么也没发生过一样凭空消失了.

句柄是归约过程中某一个产生式右边的串. 句柄的右侧一定全部是终结符.

比如 $S\Rightarrow aABe\Rightarrow aAde\Rightarrow aAbcde\Rightarrow abbcde$, 第一步归约 $A\leftarrow b$ 的句柄是 $b$, 第二步归约 $A\leftarrow Abc$ 的句柄是 $Abc$.

从第一个符号到句柄为止的子串称为活前缀 (包括空串和本身).

和自上而下方法一样, 自下而上方法也只能适用于部分上下文无关文法.

自上而下方法要消除左递归, 左因子, 然而自下而上方法可以有左递归和左因子; 自下而上方法面临的问题主要是移进-归约冲突和归约-归约冲突.

悬空 else 代表的二义性问题在自下而上分析中也存在.

LR 文法 (或者叫 LR(1) 文法) 是一种特殊的自下而上方法, 包括 SLR, LR, LALR 三种. 和 LL 文法不同, 这个不太容易用几行话定义.

LR 的 L 指的是从左向右扫描输入, R 指的是最右边推导, 省略的 (1) 指的是每步动作向前查看的符号个数为 1.

LR 分析器的核心是查看当前"状态"和输入符号共同决定下一步动作, 到底是移进还是归约.

比如当前分析器状态是 0, 输入符号为 id 执行的动作是移进, 分析器的状态改变成了 1; 接下来输入符号为 +, 1 状态下的分析器遇到 + 恰好会按照产生式 F->id 归约; 那么我们把和 id 相关的一切都清除 (包括状态 1), 而是用新的 F 去替代 (仿佛从未有过 id 这个符号).

以上这些动作等价于当前分析器状态是 0, 输入符号为 F 执行的动作是移进, 分析器改变成了新的状态, 以此类推.

换句话说, 归约把当前状态回退至之前的某个状态, 再移进一个非终结符发生状态转移.

可见, LR 分析表应该长这样:

让我们来画出文法 E->E+T, E->T, T->T*F, T->F, F->(E), F->id 的 SLR 分析表.

第一步 构建项目集规范族.

形如 $A\rightarrow X\cdot Y$ 这种形式的式子称为 LR(0) 项目 (简称项目), 点左侧代表已经推出的历史信息, 点右侧代表还未推出的希望愿景. 这个式子说明分析器已经输入了一个 $X$, 如果再得到一个 $Y$ (移进) 就可以变成 $A\rightarrow XY\cdot$. 点在最右侧通常意味着可以归约, 因为已经看到了所有的希望愿景.

为什么把这种式子称作 LR(0) 项目呢. 是因为仅到目前为止, 这种方法只根据当前的式子和输入符号执行动作, 而不考虑后续的输入符号.

让我们从文法的开始符号 E 开始.

哦, 出问题了. 归约是反着进行的, 因为有 E->E+T 这种式子, 我们没办法通过判定归约途中出现了 E 是否就应该结束. 那额外引入一个拓广符号 E', 规定 E'->E 是文法起点吧.

首先我们应该有

\[E'\rightarrow\cdot E \]

$E$ 是一个非终结符, $E'$ 期待的愿景会不会是它所推导的 $E$ 所推导的符号呢? 于是加入

\[\begin{aligned} &E'\rightarrow\cdot E\\\\ &E\rightarrow \cdot E+T\\\\ &E\rightarrow\cdot T \end{aligned} \]

同样地, $T$ 的愿景会不会层层传递到 $E'$ 呢? 于是加入

\[\begin{aligned} &E'\rightarrow\cdot E\\\\ &E\rightarrow \cdot E+T\\\\ &E\rightarrow\cdot T\\\\ &T\rightarrow\cdot T*F\\\\ &T\rightarrow\cdot F \end{aligned} \]

让我们继续对 $F$ 作同样的步骤:

\[\begin{aligned} &E'\rightarrow\cdot E\\\\ &E\rightarrow \cdot E+T\\\\ &E\rightarrow\cdot T\\\\ &T\rightarrow\cdot T*F\\\\ &T\rightarrow\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

以上这个仅由初始状态得到的 LR(0) 项目集被记作状态 $I_0$. 事实上只要点出现在非终结符前面, 就要全部将其展开.

可以看到, $I_0$ 可以接受 $\{E, T, F, (, \text{id}\}$ (移进) 作为下一个输入符号.

那就继续这个无比繁琐还容易写错的过程!

设 $I_0$ 接受 $E$ 变为状态 $I_1$:

\[\begin{aligned} &E'\rightarrow E\cdot \\\\ &E\rightarrow E\cdot+T \end{aligned} \]

设 $I_0$ 接受 $T$ 变为状态 $I_2$:

\[\begin{aligned} &E'\rightarrow T\cdot \\\\ &T\rightarrow T\cdot *F \end{aligned} \]

设 $I_0$ 接受 $F$ 变为状态 $I_3$:

\[T\rightarrow F\cdot \]

设 $I_0$ 接受 $($ 变为状态 $I_4$:

\[F\rightarrow (\cdot E) \]

点移动到了非终结符 $E$ 的前面, 因此还要加入 $E$ 的愿景:

\[\begin{aligned} &F\rightarrow (\cdot E)\\\\ &E\rightarrow \cdot E+T\\\\ &E\rightarrow\cdot T\\\\ &T\rightarrow\cdot T*F\\\\ &T\rightarrow\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

设 $I_0$ 接受 $\text{id}$ 变为状态 $I_5$:

\[F\rightarrow \text{id}\cdot \]

$I_0$ 的状态转移处理好了. 接下来处理 $I_1$.

$I_1$ 可以接受 $\{+\}$ (移进) 作为下一个输入符号.

设 $I_1$ 接受 $+$ 变为状态 $I_6$:

\[E\rightarrow E+\cdot T \]

点移动到了非终结符 $T$ 的前面, 因此还要加入 $T$ 的愿景:

\[\begin{aligned} &E\rightarrow E+\cdot T\\\\ &T\rightarrow\cdot T*F\\\\ &T\rightarrow\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

$I_1$ 的状态转移处理好了. 接下来处理 $I_2$.

$I_2$ 可以接受 $\{*\}$ (移进) 作为下一个输入符号.

设 $I_2$ 接受 $*$ 变为状态 $I_7$:

\[T\rightarrow T*\cdot F \]

点移动到了非终结符 $F$ 的前面, 因此还要加入 $F$ 的愿景:

\[\begin{aligned} &T\rightarrow T*\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

$I_2$ 的状态转移处理好了. 接下来处理 $I_3$. 诶, $I_3$ 接受不了任何符号. 接下来处理 $I_4$.

$I_4$ 可以接受 $\{E,T,F,(,\text{id}\}$ (移进) 作为下一个输入符号.

设 $I_4$ 接受 $E$ 变为状态 $I_8$:

\[\begin{aligned} & F\rightarrow (E\cdot)\\\\ & E\rightarrow E\cdot +T \end{aligned} \]

设 $I_4$ 接受 $T$ 变为状态 $I_9$:

\[\begin{aligned} &E'\rightarrow T\cdot \\\\ &T\rightarrow T\cdot *F \end{aligned} \]

这个和 $I_2$ 相同, 就不重复定义了.

设 $I_4$ 接受 $F$ 变为状态 $I_9$:

\[T\rightarrow F\cdot \]

这个和 $I_3$ 相同, 就不重复定义了.

设 $I_4$ 接受 $($ 变为状态 $I_9$:

这个就是 $I_4$ 自己, 就不重复定义了.

设 $I_4$ 接受 $\text{id}$ 变为状态 $I_9$:

\[F\rightarrow \text{id}\cdot \]

这个和 $I_5$ 相同, 就不重复定义了.

$I_4$ 的状态转移处理好了. 接下来处理 $I_5$. 诶, $I_5$ 接受不了任何符号. 接下来处理 $I_6$.

$I_6$ 可以接受 $\{,T,F,(,\text{id}\}$ (移进) 作为下一个输入符号.

设 $I_6$ 接受 $T$ 变为状态 $I_9$:

\[\begin{aligned} &E\rightarrow E+T\cdot \\\\ &T\rightarrow T\cdot * F \end{aligned} \]

设 $I_6$ 接受 $F$ 变为状态 $I_{10}$:

\[T\rightarrow F\cdot \]

这个和 $I_3$ 相同, 就不重复定义了.

设 $I_6$ 接受 $($ 变为状态 $I_{10}$:

这个和 $I_4$ 相同, 就不重复定义了.

设 $I_6$ 接受 $\text{id}$ 变为状态 $I_{10}$:

\[F\rightarrow \text{id}\cdot \]

这个和 $I_5$ 相同, 就不重复定义了.

$I_6$ 的状态转移处理好了. 接下来处理 $I_7$.

$I_7$ 可以接受 $\{F,(,\text{id}\}$ (移进) 作为下一个输入符号.

设 $I_7$ 接受 $F$ 变为状态 $I_{10}$:

\[T\rightarrow T*F\cdot \]

设 $I_7$ 接受 $($ 变为状态 $I_{11}$:

这个和 $I_4$ 相同, 就不重复定义了.

设 $I_7$ 接受 $\text{id}$ 变为状态 $I_{11}$:

\[F\rightarrow \text{id}\cdot \]

这个和 $I_5$ 相同, 就不重复定义了.

$I_7$ 的状态转移处理好了. 接下来处理 $I_8$.

$I_8$ 可以接受 $\{),+\}$ (移进) 作为下一个输入符号.

设 $I_8$ 接受 $)$ 变为状态 $I_{11}$:

\[F\rightarrow (E)\cdot \]

设 $I_8$ 接受 $+$ 变为状态 $I_{12}$:

\[\begin{aligned} &E\rightarrow E+\cdot T\\\\ &T\rightarrow\cdot T*F\\\\ &T\rightarrow\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

这个和 $I_6$ 相同, 就不重复定义了.

$I_8$ 的状态转移处理好了. 接下来处理 $I_9$.

$I_9$ 可以接受 $\{*\}$ (移进) 作为下一个输入符号.

设 $I_9$ 接受 $*$ 变为状态 $I_{12}$:

\[\begin{aligned} &T\rightarrow T*\cdot F\\\\ &F\rightarrow\cdot (E)\\\\ &F\rightarrow \cdot \text{id} \end{aligned} \]

这个和 $I_7$ 相同, 就不重复定义了.

$I_9$ 的状态转移处理好了. 接下来处理 $I_{10}$. 诶, $I_{10}$, $I_{11}$ 都接受不了任何符号.

项目集规范族到此构建完成, 从中也可以画出完整的 DFA.

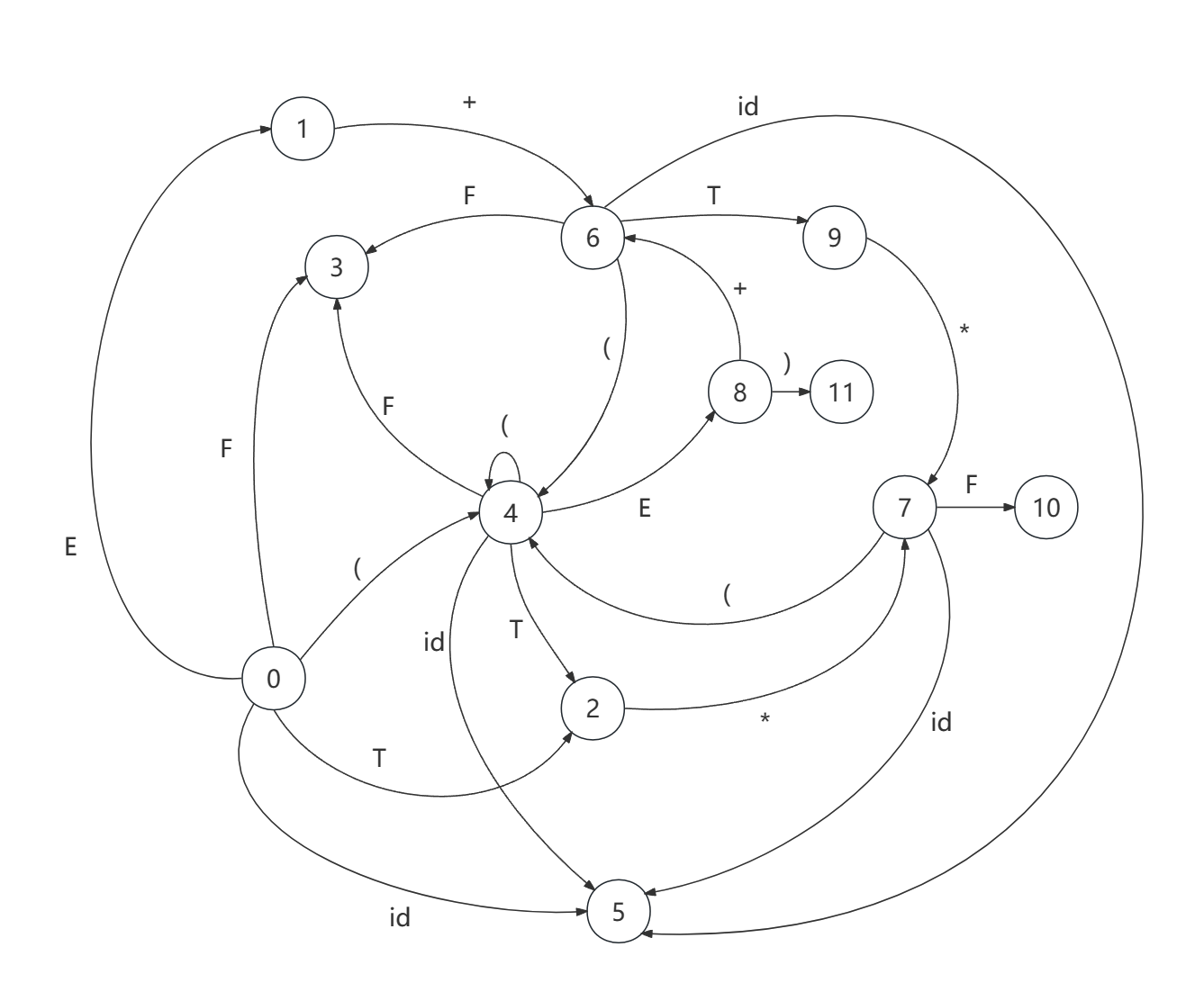
可以证明这个 DFA 不是平面图, 也就是做不到边不相交 (笑).

第二步 建立分析表.

对于移进的情形 (如 $A\rightarrow \cdot\alpha$), 全部根据上述 DFA 写入分析表即可.

对于归约的情形 (如 $A\rightarrow \alpha\cdot$), SLR 给出的策略是把 $FOLLOW(A)$ 的所有元素采用 $A\rightarrow \alpha$ 归约. 因为此时点已经到头了, 这个状态下遇到任意一个合法的符号 (也就是 $FOLLOW(A)$ 中的元素) 都应该归约.

这种根据 FOLLOW 集来归约是 SLR 方法的最大特点. 这也是 SLR(1) 与 LR(0) 的不同之处 (LR(0) 文法不考虑 FOLLOW 集合).

考虑状态 i0, 移进动作 (shift action) 是 i0 -> i5 (id), i0 -> i4 ((); 转移 (goto) 是 i0 -> i1 (E), i0 -> i2 (T), i0 -> i3 (F).

为什么 action 要强调 s 或者 r? 因为每输入一个终结符都可能移进或归约; 为什么 goto 只写数字? 因为非终结符一定是归约得到的.

考虑状态 i1, 移进动作是 i1 -> i6 (+), 归约动作 (reduce action) 是 E' -> E, E' 的 FOLLOW 集为 {$}. 这个由文法开始符号归约的情况作为 acc 接受状态.

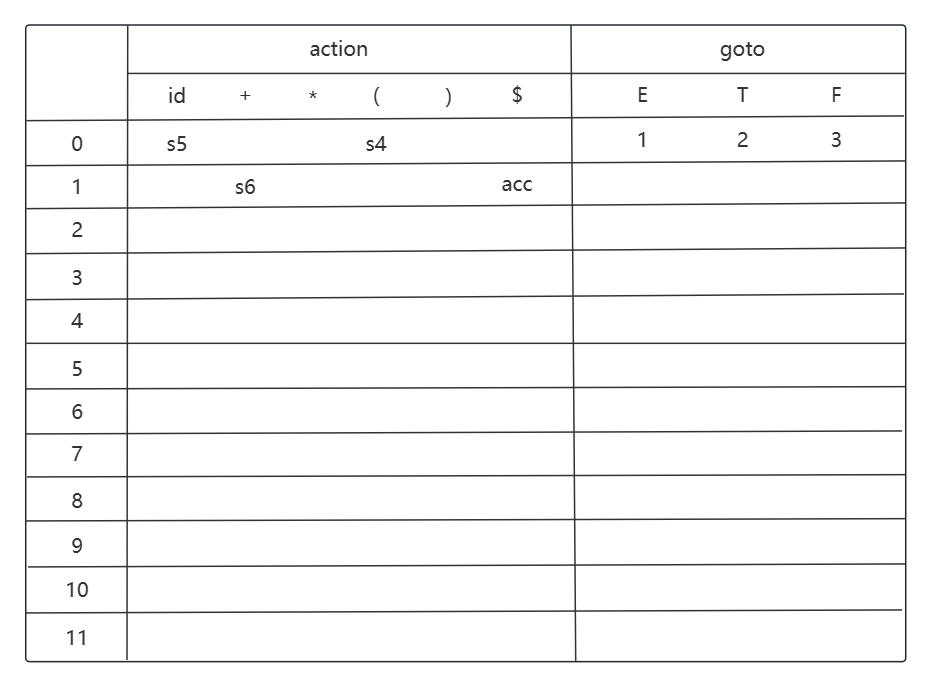
考虑状态 i2, 移进动作是 i2 -> i7 (*), 归约动作是 E -> T, E 的 FOLLOW 集为 {+, ), $}.

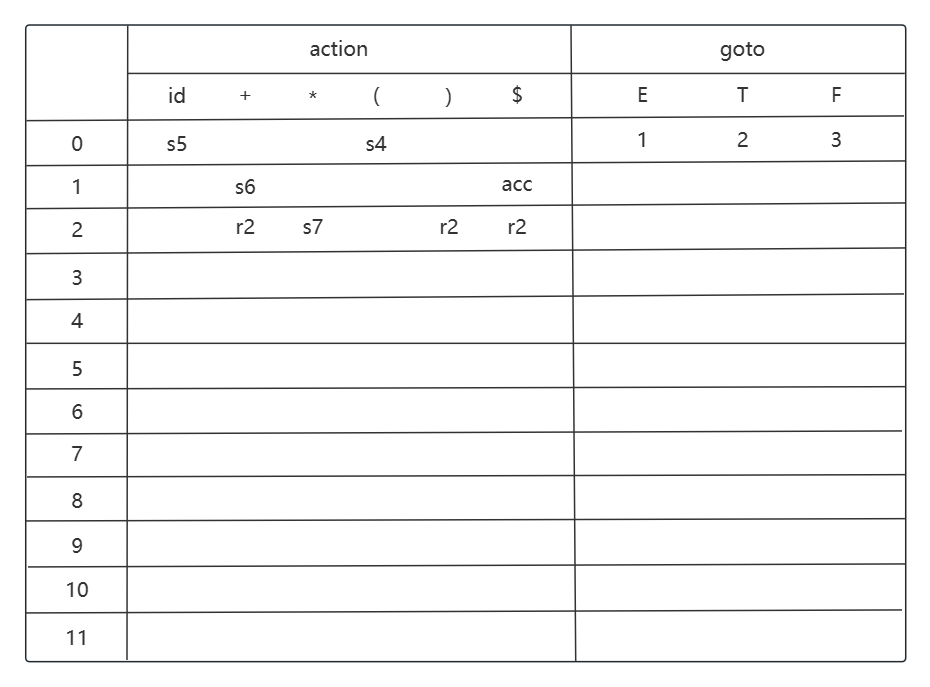
考虑状态 i3, 归约动作是 T -> F, T 的 FOLLOW 集为 {+, *, ), $}.

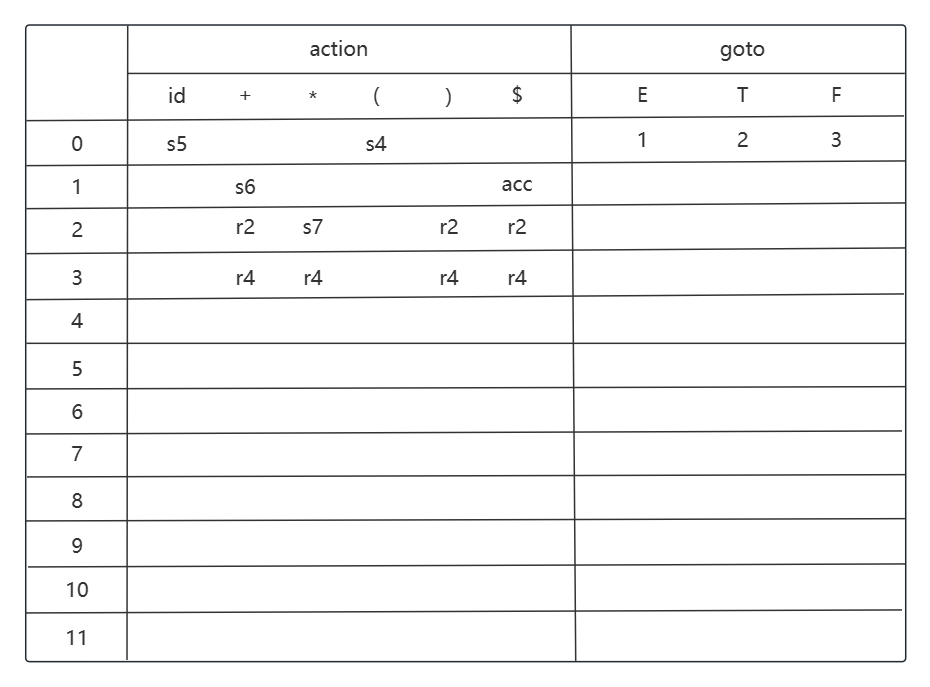
考虑状态 i4, 移进动作是 i4 -> i5 (id), i4 -> i4 ((); 转移是 i4 -> i8 (E), i4 -> i2 (T), i4 -> i3 (F).

考虑状态 i5, 归约动作是 F -> id, F 的 FOLLOW 集为 {+, *, ), $}.

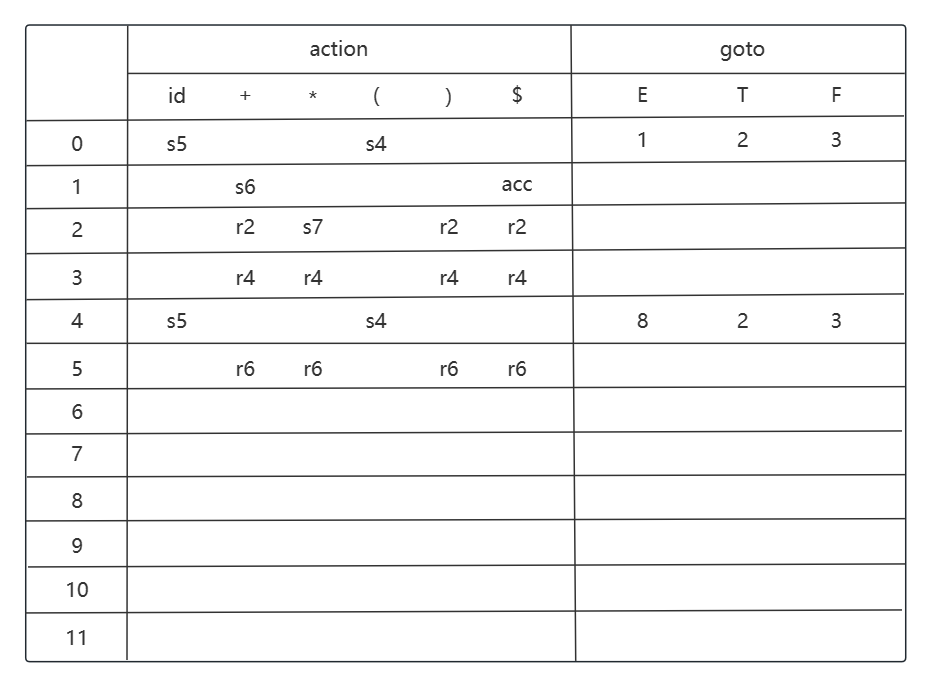
考虑状态 i6, 移进动作是 i6 -> i5 (id), i6 -> i4 ((); 转移是 i6 -> i9 (T), i6 -> i3 (F).

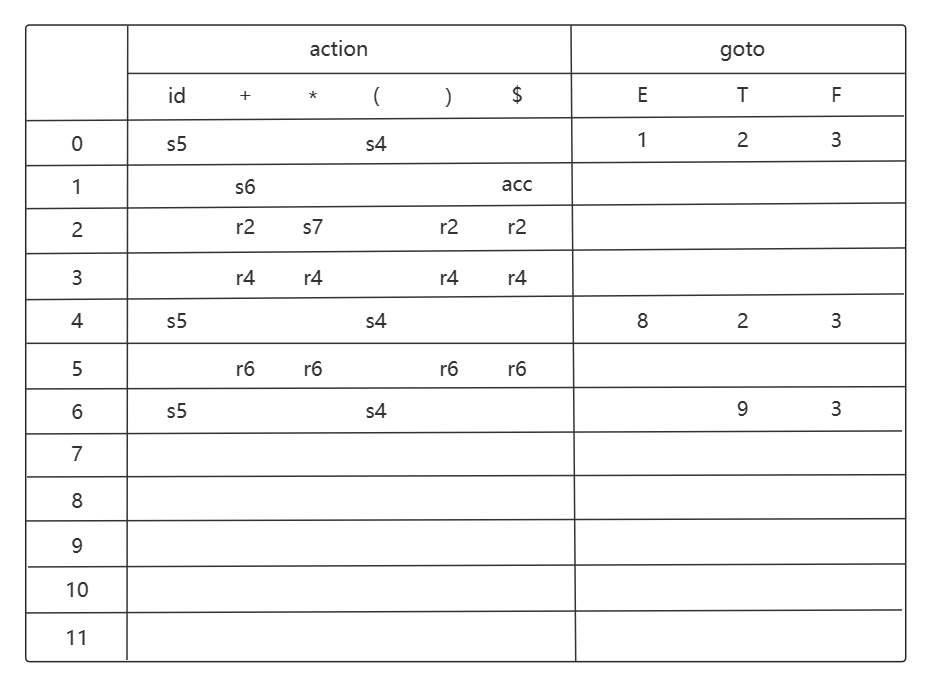
考虑状态 i7, 移进动作是 i7 -> i5 (id), i7 -> i4 ((); 转移是 i7 -> i10 (F).

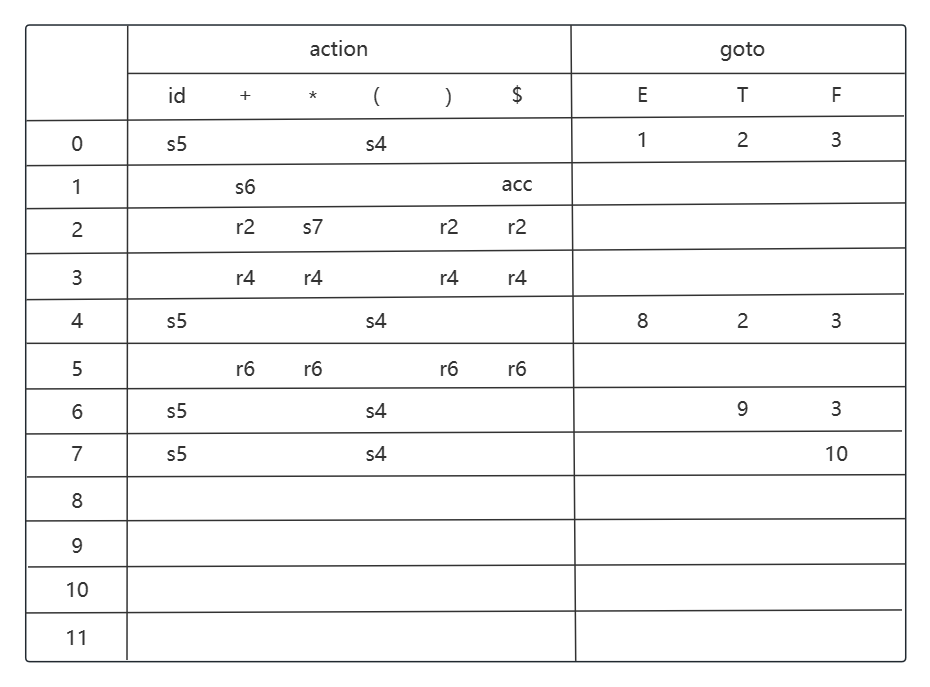
考虑状态 i8, 移进动作是 i8 -> i6 (+), i8 -> i11 ()).

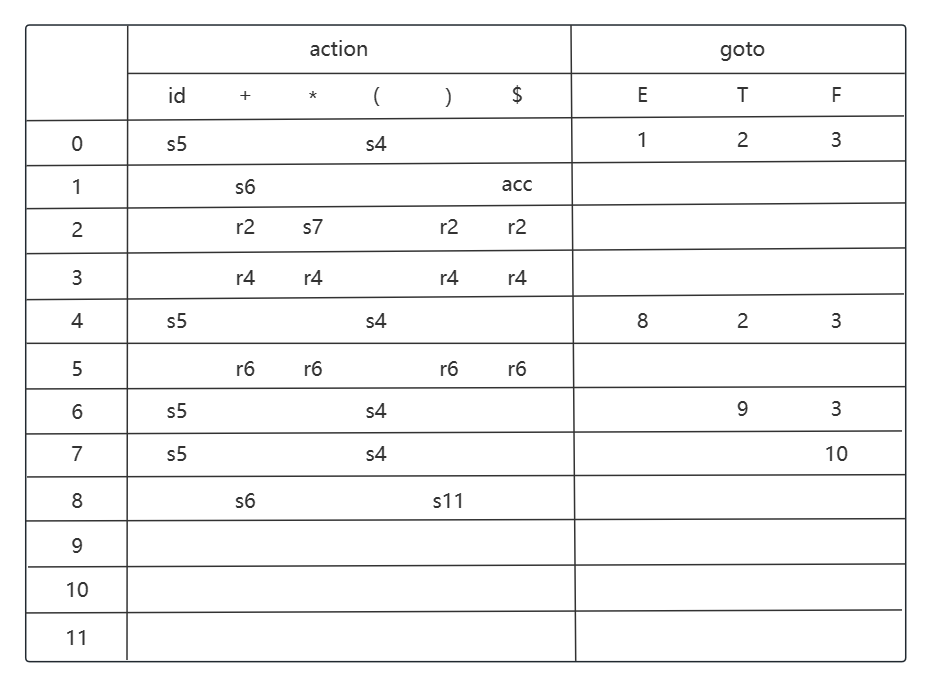
考虑状态 i9, 移进动作是 i9 -> i7 (*), 归约动作是 E -> E + T, E 的 FOLLOW 集为 {+, ), $}.

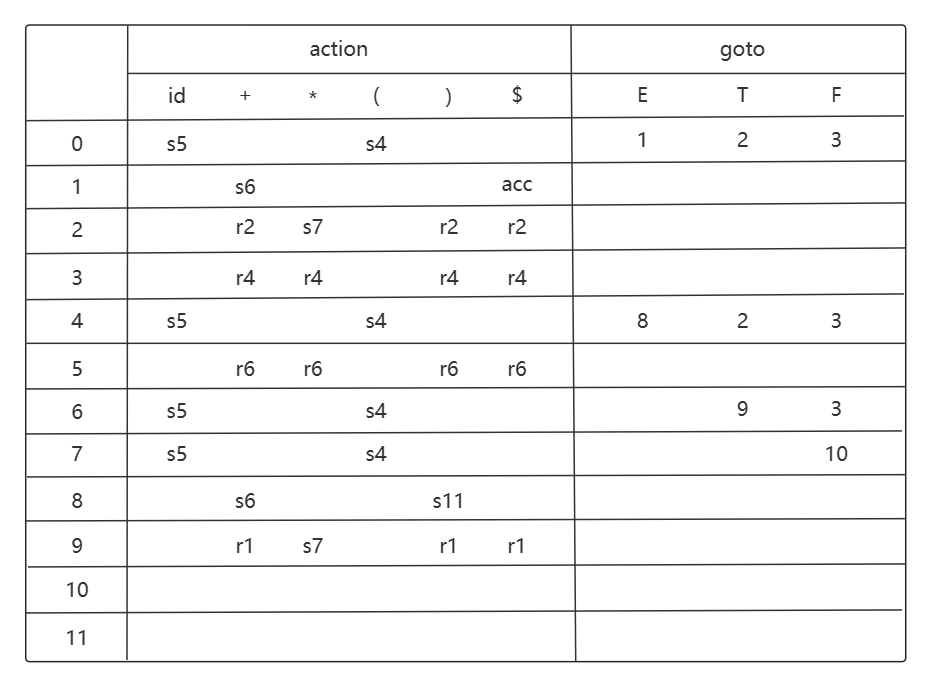
考虑状态 i10, 归约动作是 T -> T * F, T 的 FOLLOW 集为 {+, *, ), $}.

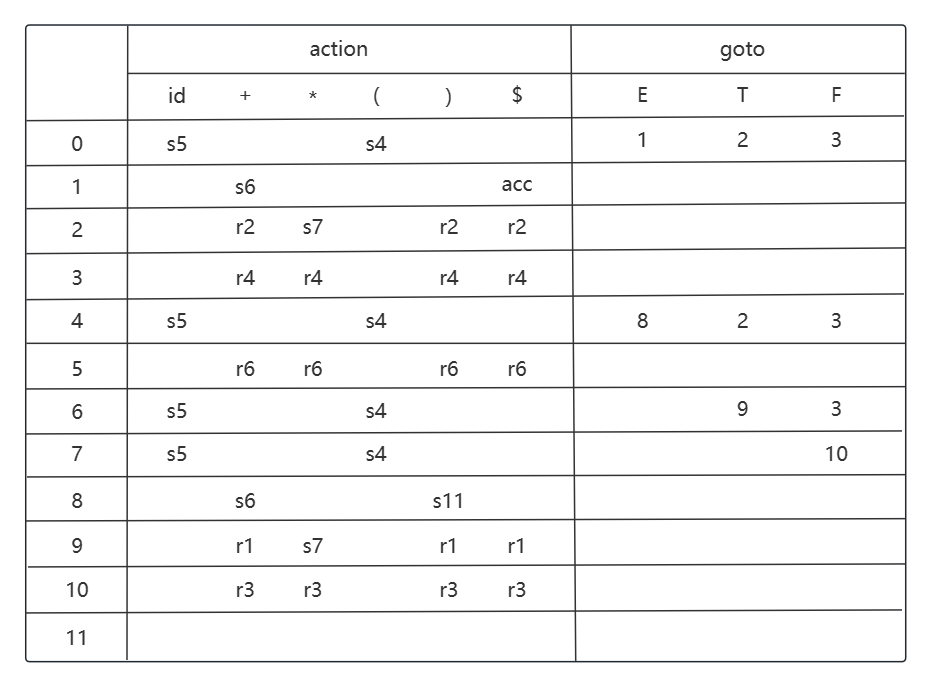
考虑状态 i11, 归约动作是 F -> (E), F 的 FOLLOW 集为 {+, *, ), $}.

以上是完整的 SLR 分析表构建过程.

事实上, SLR 经常出现移进-归约冲突, 究其原因是归约策略 too young too simple 了. 怎么能一律把 FOLLOW 集中的所有元素都按照当前的产生式归约呢. 这时就有了最完善的 LR 方法.

定义前向搜索符为归约后希望看到的终结符. 本质上, 前向搜索符只是"点"后面的 FOLLOW 集. 前向搜索符写在 LR(0) 项目的后面, 用逗号分隔开.

举个例子 $S \rightarrow BB, B \rightarrow bB | a$.

使用前向搜索符的 $I_0$ 状态应该是

\[\begin{aligned} &S'\rightarrow \cdot S,\quad \$\\\\ &S\rightarrow\cdot B_1 B_2,\quad \$\\\\ & B_1\rightarrow \cdot bB_3,\quad a|b\\\\ & B_1\rightarrow \cdot a,\quad a|b \end{aligned} \]

如果这时接受了一个 $B$, 那么新的状态 $I_0'$ 应该是

\[\begin{aligned} &S\rightarrow B_1\cdot B_2,\quad \$\\\\ & B_2\rightarrow \cdot bB_3,\quad \$\\\\ & B_2\rightarrow \cdot a,\quad \$ \end{aligned} \]

在 DFA 建立完成后, 归约动作只会根据式子后面的前向搜索符来执行, 而不是全部的 FOLLOW 集.

LR 方法正是采用这种前向搜索策略.

LALR 方法则是在 LR 的基础上, 合并了所有仅前向搜索符不同的项目集. 这被称为同心项目集.

比如 LR 中有两个状态 $\displaystyle{I_1:B\rightarrow b\cdot B,\text{ }a|b}$ 和 $\displaystyle{I_2:B\rightarrow b\cdot B,\text{ }\$ }$.

LALR 会合并成一个状态 $\displaystyle{I_{12}:B\rightarrow b\cdot B,\ \ a|b|\$}$.

如有必要, 可以添加错误恢复.

对分析器的每个状态添加一个错误处理例程, 比如期待输入运算对象时输入了别的符号, 那么直接转移到正确输入时本应该到达的状态, 或者直接删掉输入符号, 然后将这个例程写进分析表中.

自下而上的文法分析至此结束.

2.5 语法制导

每个文法产生式 $A\rightarrow \alpha$ 都有一个语义规则, 形式为 $b=f(c_1,c_2,\cdots,c_k)$, 其中 $b, c_i$ 为属性.

如果 $b$ 是 $A$ 的属性, 那么通常称为综合属性 (由子节点计算父节点, 缩写为 s, synthesize). 综合属性通常代表一个函数的返回值.

如果 $b$ 是 $\alpha$ 中的某个属性, 那么通常称为继承属性 (由父节点或兄弟节点计算得到, 缩写为 i, inherit). 继承属性通常代表一个函数的参数.

语法制导的定义使每一个产生式都对应一个语义规则.

每个节点的属性值都标注的分析树称为注释分析树. 注释分析树不会改变原先分析树的结构.

仅使用综合属性的语法制导定义称为S 属性定义 (不要少了后面两个字).

如果产生式 L -> id 的语义规则是 addType(id.entry, L.in), 这指的是将属性 L.in 添加给新的 id.entry. 这是典型的继承属性.

语法树 (AST) 是浓缩表示的分析树. 构造语法树的语法制导定义有三种函数:

mkLeaf(id, entry): 建立标记为 id 的标识符节点, 值为 entry, 是指向该节点的指针.
mkLeaf(num, val): 建立标记为 num 的整数节点, 值为 val.
mkNode(op, left, right): 建立标记为 op 的非叶节点, left 和 right 分别是左子树和右子树的指针, 通常代表一个运算符.