526互联

2023冲刺国赛模拟 13.1

发布时间 2023-06-06 18:59:07作者: KafuuChinocpp

T1 铲雪

通过打表可以发现 \(2^{23}\equiv 2^{47}\pmod{998244352}\) ，因此对于前 \(22\) 次平方操作，直接暴力修改即可，超出 \(22\) 的平方操作，对每个位置维护长度为 \(24\) 的平方数组，那么每次操作就是简单的数组循环移动，线段树维护即可。

code 
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <map>
#include <iostream>
using namespace std;
const int max1 = 1e5;
const int mod = 998244353;

int n, m, A[max1 + 5][24];

void Add ( int &x, int y )
{
    x += y;
    if ( x >= mod )
        x -= mod;
    return;
}

int Quick_Power ( int base, int p )
{
    int res = 1;
    while ( p )
    {
        if ( p & 1 )
            res = 1LL * res * base % mod;
        p >>= 1;
        base = 1LL * base * base % mod;
    }
    return res;
}

map <int, int> pos;

struct Bit
{
    int tree[max1 + 5];

    #define lowbit(now) ( now & -now )

    void Clear ()
    {
        memset(tree + 1, 0, sizeof(int) * n);
        return;
    }

    void Insert ( int now, int x )
    {
        while ( now <= n )
        {
            Add(tree[now], x);
            now += lowbit(now);
        }
        return;
    }

    int Query ( int now )
    {
        int res = 0;
        while ( now )
        {
            Add(res, tree[now]);
            now -= lowbit(now);
        }
        return res;
    }

    int Query ( int L, int R )
    {
        return ( Query(R) - Query(L - 1) + mod ) % mod;
    }
}Tree1;

struct Segment_Tree
{
    #define lson(now) ( now << 1 )
    #define rson(now) ( now << 1 | 1 )

    struct Data
    {
        int val[24], head, tag;
    }tree[max1 * 4 + 5];

    void Push_Up ( int now )
    {
        tree[now].head = 0;
        int L = tree[lson(now)].head, R = tree[rson(now)].head;
        for ( int i = 0; i < 24; i ++ )
        {
            tree[now].val[i] = 0;
            Add(tree[now].val[i], tree[lson(now)].val[L]);
            Add(tree[now].val[i], tree[rson(now)].val[R]);
            L = L == 23 ? 0 : L + 1;
            R = R == 23 ? 0 : R + 1;
        }
        return;
    }

    void Push_Down ( int now )
    {
        if ( tree[now].tag )
        {
            tree[lson(now)].head = ( tree[lson(now)].head + tree[now].tag ) % 24;
            tree[rson(now)].head = ( tree[rson(now)].head + tree[now].tag ) % 24;
            tree[lson(now)].tag += tree[now].tag;
            tree[rson(now)].tag += tree[now].tag;
            tree[now].tag = 0;
        }
        return;
    }

    void Build ( int now, int L, int R )
    {
        memset(tree[now].val, 0, sizeof(tree[now].val)); tree[now].head = tree[now].tag = 0;
        if ( L == R )
            return;
        
        int mid = L + R >> 1;
        Build(lson(now), L, mid);
        Build(rson(now), mid + 1, R);
        return;
    }

    void Insert ( int now, int L, int R, int p, int x )
    {
        if ( L == R )
        {
            tree[now].head = tree[now].tag = 0; tree[now].val[0] = x;
            for ( int i = 1; i < 24; i ++ )
                tree[now].val[i] = 1LL * tree[now].val[i - 1] * tree[now].val[i - 1] % mod;
            return;
        }

        Push_Down(now);
        int mid = L + R >> 1;
        if ( p <= mid )
            Insert(lson(now), L, mid, p, x);
        else
            Insert(rson(now), mid + 1, R, p, x);
        Push_Up(now);
        return;
    }

    void Update ( int now, int L, int R, int ql, int qr )
    {
        if ( L >= ql && R <= qr )
        {
            tree[now].head = tree[now].head == 23 ? 0 : tree[now].head + 1;
            ++tree[now].tag;
            return;
        }

        Push_Down(now);
        int mid = L + R >> 1;
        if ( ql <= mid )
            Update(lson(now), L, mid, ql, qr);
        if ( qr > mid )
            Update(rson(now), mid + 1, R, ql, qr);
        Push_Up(now);
        return;
    }

    int Query ( int now, int L, int R, int ql, int qr )
    {
        if ( L >= ql && R <= qr )
            return tree[now].val[tree[now].head];
        
        Push_Down(now);
        int mid = L + R >> 1, res = 0;
        if ( ql <= mid )
            Add(res, Query(lson(now), L, mid, ql, qr));
        if ( qr > mid )
            Add(res, Query(rson(now), mid + 1, R, ql, qr));
        return res;
    }
}Tree2;

int main ()
{
    freopen("snow.in", "r", stdin);
    freopen("snow.out", "w", stdout);

    scanf("%d%d", &n, &m); Tree1.Clear(); Tree2.Build(1, 1, n);
    for ( int i = 1; i <= n; i ++ )
    {
        scanf("%d", &A[i][0]);
        A[i][0] = Quick_Power(A[i][0], mod - 2);
        for ( int k = 1; k < 24; k ++ )
            A[i][k] = 1LL * A[i][k - 1] * A[i][k - 1] % mod;
        pos[i] = 0; Tree1.Insert(i, A[i][0]);
    }

    pos[n + 1] = 0;

    int opt, L, R, ans;
    while ( m -- )
    {
        scanf("%d%d%d", &opt, &L, &R);
        if ( !opt )
        {
            Tree2.Update(1, 1, n, L, R);

            while ( true )
            {
                int p = pos.lower_bound(L) -> first;
                if ( p > R )
                    break;

                L = p + 1;
                Tree1.Insert(p, mod - A[p][pos[p]]);
                if ( pos[p] == 22 )
                {
                    pos.erase(pos.find(p));
                    Tree2.Insert(1, 1, n, p, A[p][23]);
                }
                else
                {
                    ++pos[p];
                    Tree1.Insert(p, A[p][pos[p]]);
                }
            }
        }
        else
        {
            ans = ( Tree1.Query(L, R) + Tree2.Query(1, 1, n, L, R) ) % mod;
            printf("%d\n", ans);
        }
    }

    return 0;
}

T2 抽卡

设 \(f(S)\) 表示当前先手行动，剩余卡牌组成集合 \(S\) 时的期望权值和，设 \(g(S)\) 表示当前后手行动，剩余卡牌组成集合 \(S\) 时的期望权值和。

考虑转移，以 \(f(S)\) 转移为例，枚举随机选取的集合 \(T\) （由于 \(T\) 越大，可选卡牌越多，因此先手会使 \(T\) 集合尽可能大），设合法的 \(T\) 集合有 \(cnt\) 个，存在转移：

\[f(S)=\tfrac{1}{cnt}\sum_{T\subseteq S, |T|\le m}\max(\max_{i\in T}(a_i+g(S-\{i\})), g(S)) \]

同理：

\[g(S)=\tfrac{1}{cnt}\sum_{T\subseteq S, |T|\le m}\min(\min_{i\in T}(a_i+f(S-\{i\})), f(S)) \]

容易发现转移存在后效性，比较显然的思路使枚举 \(f(S)\) 的值，带入计算，找到计算结果与枚举结果相等的值。

优化只需要发现随之枚举值的增大，求解值同样增大，但是求解值增大速度较小，简单画函数图像可以发现求解值与枚举值之差存在单调性，因此可以二分求解。

code 
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;

const int max1 = 15, max2 = 1 << 15;
const double eps = 1e-8;

int n, m, k, A[max1 + 5], sum;
vector <int> sit[max2 + 5];
double f[max2 + 5], g[max2 + 5], tmp1[max2 + 5], tmp2[max2 + 5];

void Solve ( int S, double val )
{
    int siz = sit[S].size();
    g[S] = 0;
    for ( auto T : sit[S] )
        g[S] += min(tmp1[T], val) / siz;

    f[S] = 0;
    for ( auto T : sit[S] )
        f[S] += max(tmp2[T], g[S]) / siz;

    return;
}

int main ()
{
    freopen("card.in", "r", stdin);
    freopen("card.out", "w", stdout);

    scanf("%d%d%d", &n, &m, &k);
    for ( int i = 1; i <= n; i ++ )
        scanf("%d", &A[i]), sum += A[i];

    for ( int S = 0; S < 1 << n; S ++ )
    {
        if ( __builtin_popcount(S) >= k )
        {
            if ( __builtin_popcount(S) <= m )
                sit[S].push_back(S);
            else
            {
                for ( int T = S; T; T = ( T - 1 ) & S )
                    if ( __builtin_popcount(T) == m )
                        sit[S].push_back(T);
            }
        }
    }

    for ( int S = 0; S < 1 << n; S ++ )
    {
        int pop = __builtin_popcount(S);
        if ( pop == k )
            f[S] = g[S] = 0;
        else if ( pop > k )
        {
            for ( auto T : sit[S] )
            {
                tmp1[T] = sum;
                for ( int i = 1; i <= n; i ++ )
                    if ( T >> i - 1 & 1 )
                        tmp1[T] = min(tmp1[T], A[i] + f[S ^ 1 << i - 1]);
            }

            for ( auto T : sit[S] )
            {
                tmp2[T] = -sum;
                for ( int i = 1; i <= n; i ++ )
                    if ( T >> i - 1 & 1 )
                        tmp2[T] = max(tmp2[T], A[i] + g[S ^ 1 << i - 1]);
            }

            double L = 0, R = sum;
            while ( R - L > eps )
            {
                double mid = 0.5 * ( L + R ); Solve(S, mid);
                if ( f[S] < mid )
                    R = mid;
                else
                    L = mid;
            }
        }
    }

    printf("%.8lf\n", f[( 1 << n ) - 1]);

    return 0;
}

T3 樟

考虑一条边 \((i, j)\) ，根据题目要求，一定存在边 \((p_i, p_j)\) ，继续推导，一定存在边 \((p_{p_i}, p_{p_j})\) ，继续推导，一定存在边 \((p_{p_{p_i}}, p_{p_{p_j}})\) ，容易发现这构成置换环的关系。

于是考虑两个置换环的连边，以大小为 \(2,4\) 的置换环为例：

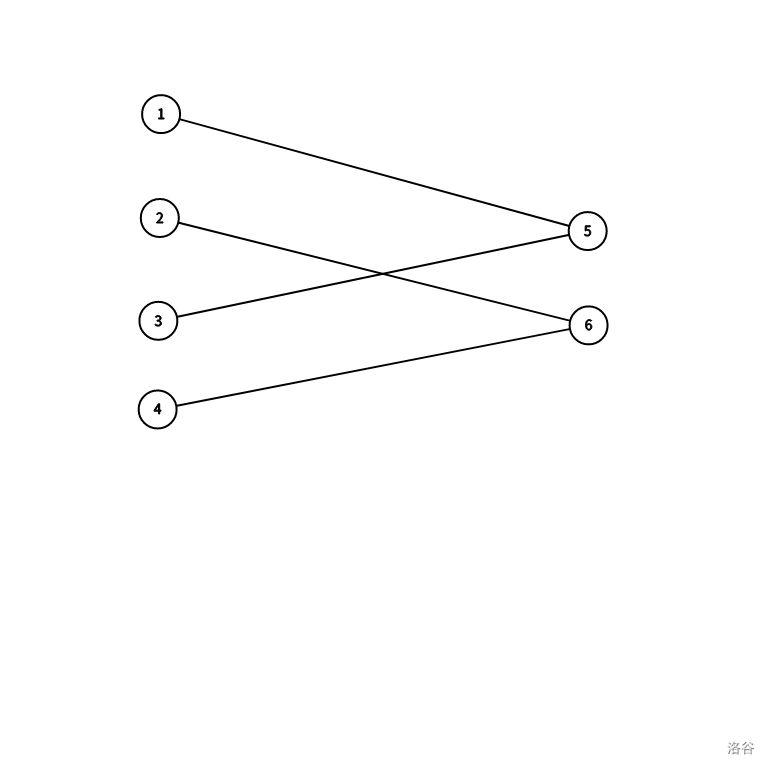
容易发现图中不存在环，因此这样的连边可能形成树。

猜想到置换环之间的连边不存在环可能与 \(\gcd\) 有关，因此考虑大小为 \(4,6\) 的置换环：

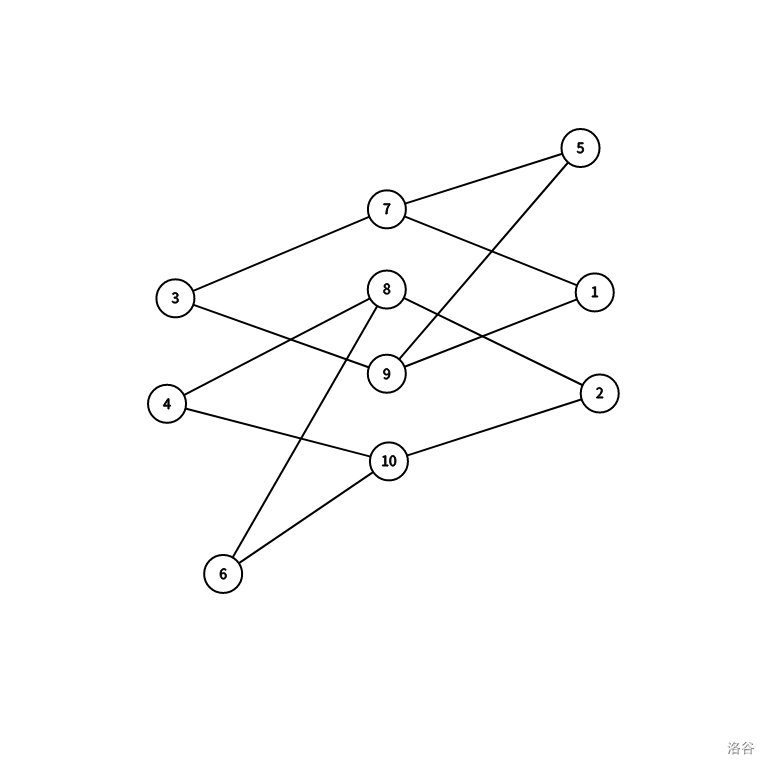
（其中 \(1, 2, 3, 4, 5, 6\) 为一个置换环， \(7, 8, 9, 10\) 位一个置换环）

容易发现连边中存在环，一定无法构成一棵树。

于是猜想一个结论：只有大小存在倍数关系的置换环间存在连边，并且连边方案数为较小的环的大小。

此时观察到，大小大于 \(2\) 的置换环中的点两两之间不能存在连边，因此如果需要将整棵树连通，需要大小为 \(1\) 或大小为 \(2\) 的置换环。

如果存在大小为 \(1\) 的置换环，显然这些置换环形成树，容易通过 prufer 序列求解这棵树的方案数。

考虑将其余大小的环挂到这棵树上，设当前枚举的大小为 \(i\) ，置换环个数为 \(c_i\) ，由于大小相同的置换环之间可能存在连边，因此需要枚举当前大小的所有置换环构成的连通块个数 \(k\) ，考虑对这个存在 \(k\) 个连通块的森林进行计数，建立虚点 \(0\) ，将森林中所有树的根节点与 \(0\) 连边，容易发现此时形成的新树中，存在 \(k-1\) 个位置在 prufer 序列上数值为 \(0\) ，其余位置任意，因此方案数为 \(\binom{c_i-1}{k-1}c_i^{c_i-k}\) 。

因此大小为 \(i\) 的置换环对答案的贡献为

\[\sum_{k=1}^{c_i}\binom{c_i-1}{k-1}c_i^{c_i-k}\times i^{c_i-k}\times (\sum_{d|i, d<i}(c_d\times d))^k \]

如果不存在大小为 \(1\) 的置换环，考虑使用大小为 \(2\) 的置换环进行代替，这些环构成树的方案数为 \((2c_2)^{c_2-1}\) ，之后仍然枚举剩余大小的环连接到树上即可。

code 
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int max1 = 5e5;
const int mod = 998244353;

int T, n, A[max1 + 5], bin[max1 + 5], sum[max1 + 5];
bool vis[max1 + 5];
int fac[max1 + 5], ifac[max1 + 5], inv[max1 + 5];

int C ( int n, int m )
{
    if ( n < m || n < 0 || m < 0 )
        return 0;
    return 1LL * fac[n] * ifac[n - m] % mod * ifac[m] % mod;
}

int Quick_Power ( int base, int p )
{
    int res = 1;
    while ( p )
    {
        if ( p & 1 )
            res = 1LL * res * base % mod;
        p >>= 1;
        base = 1LL * base * base % mod;
    }
    return res;
}

void Work ()
{
    scanf("%d", &n);

    memset(bin + 1, 0, sizeof(int) * n);
    memset(sum + 1, 0, sizeof(int) * n);
    memset(vis + 1, 0, sizeof(bool) * n);

    for ( int i = 1; i <= n; i ++ )
        scanf("%d", &A[i]);

    for ( int i = 1; i <= n; i ++ )
    {
        if ( !vis[i] )
        {
            int x = i, len = 0;
            while ( !vis[x] )
            {
                ++len;
                vis[x] = true;
                x = A[x];
            }
            ++bin[len];
        }
    }

    for ( int i = 1; i <= n; i ++ )
    {
        if ( !bin[i] )
            continue;

        for ( int k = 2; k * i <= n; k ++ )
            sum[i * k] = ( sum[i * k] + 1LL * bin[i] * i ) % mod;
    }

    int ans = 0;
    if ( bin[1] )
    {
        if ( bin[1] == 1 )
            ans = 1;
        else
            ans = Quick_Power(bin[1], bin[1] - 2);

        for ( int i = 2; i <= n; i ++ )
        {
            if ( !bin[i] )
                continue;

            int trans = 0;
            for ( int k = 1; k <= bin[i]; k ++ )
                trans = ( trans + 1LL * C(bin[i] - 1, k - 1) * Quick_Power(bin[i], bin[i] - k) % mod * Quick_Power(i, bin[i] - k) % mod * Quick_Power(sum[i], k) % mod ) % mod;

            ans = 1LL * ans * trans % mod;
        }
    }
    else if ( bin[2] )
    {
        if ( bin[2] == 1 )
            ans = 1;
        else
            ans = 1LL * Quick_Power(bin[2], bin[2] - 1) * Quick_Power(2, bin[2] - 1) % mod;

        for ( int i = 3; i <= n; i ++ )
        {
            if ( !bin[i] )
                continue;

            int trans = 0;
            for ( int k = 1; k <= bin[i]; k ++ )
                trans = ( trans + 1LL * C(bin[i] - 1, k - 1) * Quick_Power(bin[i], bin[i] - k) % mod * Quick_Power(i, bin[i] - k) % mod * Quick_Power(sum[i], k) % mod ) % mod;

            ans = 1LL * ans * trans % mod;
        }
    }

    printf("%d\n", ans);
    return;
}

int main ()
{
    freopen("camphor.in", "r", stdin);
    freopen("camphor.out", "w", stdout);

    inv[1] = 1;
    for ( int i = 2; i <= max1; i ++ )
        inv[i] = 1LL * ( mod - mod / i ) * inv[mod % i] % mod;
    fac[0] = ifac[0] = 1;
    for ( int i = 1; i <= max1; i ++ )
    {
        fac[i] = 1LL * fac[i - 1] * i % mod;
        ifac[i] = 1LL * ifac[i - 1] * inv[i] % mod;
    }

    scanf("%d", &T);
    while ( T -- )
        Work();
    return 0;
}