一、问题引入
Logu P3374
模版题--树状数组。
初始化一个数组,接下来进行若干次以下操作:
- 单点修改:将某个元素的值进行修改
- 区间访问:返回该区间的总和
问题分析
如果通过简单索引操作,“1”的时间复杂度为 O(1),“2”的时间复杂度为O(n),其中如果使用一个dp表的方式来存储前n项之和,那么“2”的时间复杂度为O(1),但是一旦要进行修改操作则变成\(O(n^2)\),显然,我们需要一种更有效的数据结构来维护我们的列表
二、树状数组
我们是否可以这样想:如果我们构造一个数组,其第i个元素包含前i项之和,但是这样不适合经常修改的元素列表,我是否可以将列表划分成n份,用这n段的和来构造这个函数?
显然,如果我们进行修改操作,对其中那个数组就还是回归到了原问题上面.因此,树状数组应运而生
Lowbit操作
假设x = \((10100100)_2\),则定义:
\[lobit(x) = (100)_2 = 4
\]
即lowbit(x)表示x的二进制下从左往右数第一个1及其后面所有0(个人理解,其实就是按2的次幂为间隔划分原序列数组,只不过正好有规律,不然以其他数的次幂划分也行)
由于有符号数字在计算机中以补码的形式存在,则\(-x = (01011011)_2 + 1_2 = (01011100)_2\),发现只有lowbit(x)相同,其余都不同,于是有:
\[lobit(x) = x\&-x
\]
树状数组的构建
如图:
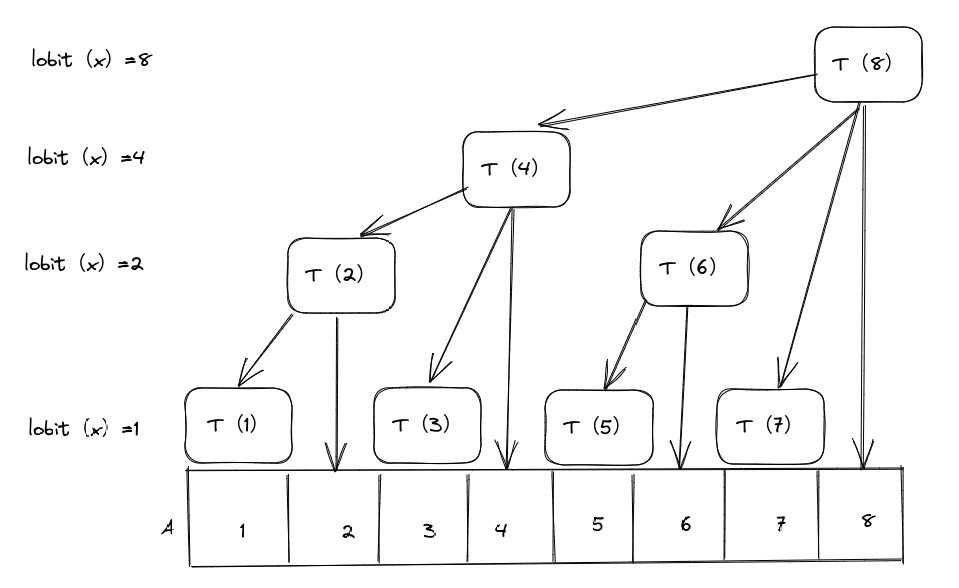
在原数组上面构建树状数组T[],观察到有如下规律:
- 对某一层数i,有lobit(x) = i,并且其子节点也为lowbit(x)
- 数最高为\(log_2 n +1\)
- 对于某一个子节点T[x],其父节点为:T[x+lowbit(x)]
- 前n个元素之和为T[n]+T[n-lowbit(n)]+T[n-lowbit(n)-lowbit(n-lowbit(n))]+....
经过如上规律,我们可以写出代码:
单点修改
void add(int x, int k) {
for (; x <= n; x += x & -x) T[x] += k;
}
区间访问
int ask(int x) {
int res = 0;
for (; x; x -= x & -x) res += T[x];
return res;
}
三、其他操作
区间修改、单点查询
我们构建一个树状数组,用来存放原数组的差分,此时该树状数组的前n项和为A[n],当我们需要对x-y之间加上或减去相同值是,在树状数组的两个元素之间只有第x个和第y+1个的值发生改变,于是只需添加:
add(x, k);
add(y+1, -k);
要进行单点查询只需求和即ask即可
区间修改、区间查询
我们知道在构建差分数组的情况下,前n项和为:
\[S = \sum_{i=1}^{x}\sum_{j=1}^{i}d[j]
\]
如图:
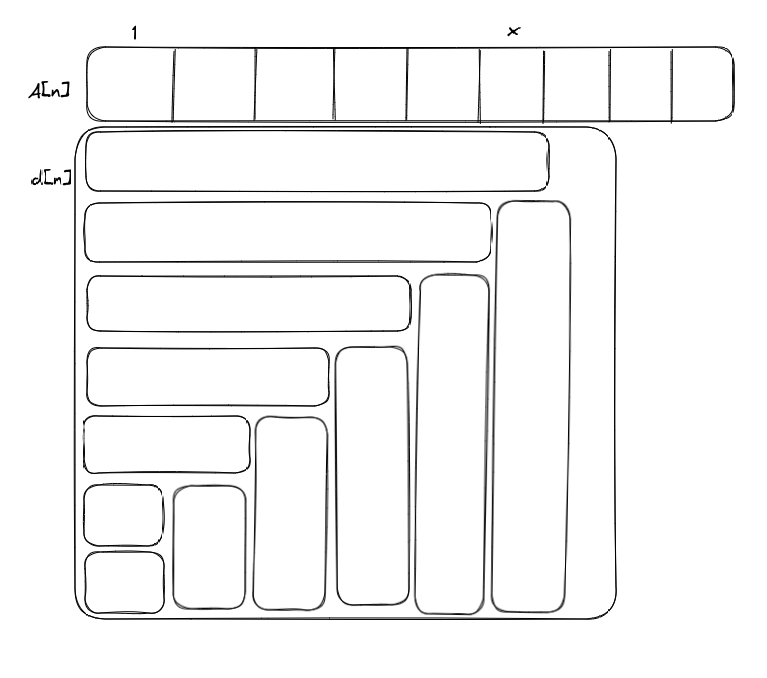
有:
\[S = \sum_{i=1}^{x}\sum_{j=1}^{i}d[j] = (1+x)\sum_{i=1}^{x}d[i] - \sum_{i=1}^{x}id[i]
\]
至于要在上面情况的基础上构建一个新的树状数组用来存储id[i]即可完成
于是有:
//区间修改
//d[i]操作不变,对新构建的id[i]:
add(x,x*k);
add(y+1,-(y+1)*k);
//区间访问:
res = (1+x)ask(x) - ask_new(x)