强化学习Chapter4——两个基本优化算法(2)
上一节,介绍了依据贝尔曼方程得出的策略迭代算法(policy iteration),本节将介绍另一种根据贝尔曼最优方程提出的,价值迭代算法(value iteration)。在此之后,本文将阐述这两种算法的共性与区别,由此总结出一种截断策略迭代算法(truncated policy iteration)。
一、价值迭代算法(value iteration)
贝尔曼最优方程形式如下:
类似上一节的思路,写成迭代的形式:
在上一节中,给定一个策略 \(\pi\),\(V^\pi\) 都是迭代方程的不动点;而在本节中,\(V^*\) 直接成为该方程的不动点,这意味着直接进行迭代,可以直接逼近 \(V^*\),这相较于策略迭代方程要简洁得多,直接得多。其收敛于不动点的证明依然留给单独的一节证明。在获得 \(V^*\) 后,获取 \(\pi^*\) 只需利用其定义式恢复即可
伪代码
def value_inter:
while delta > theta:
delta = 0
for s in S:
v = V(s)
for a in A:
V(s) = max(r(s,a) + gamma * E(V(s_next)))
delta = max(delta, |v-V(s)|)
def get_policy:
for s in S:
for a in A:
maxq = max(Q(s,a)) # 获取最大的 qsa
update_single_policy(policy, maxq, s, a) # 更新 policy 在状态 s 处的决策
return policy
二、截断策略迭代算法(truncated policy iteration)
容易发现,所谓价值迭代算法,表观上是由于仅对状态价值函数 \(V\) 进行迭代,而没有对策略进行调优。但事实上,价值迭代算法潜在地进行了策略调优——贝尔曼最优方程中的 max 符号,其实是进行了一次策略调优,即调整策略取满足 max 条件的动作 a。在这个意义上,价值迭代算法与策略迭代算法有共同之处——都在计算了价值函数 \(V\) 后调优了一次策略。
从某种程度上来讲,策略迭代算法是以单调有界来保证收敛,而价值迭代算法是通过贝尔曼最优方程来保证收敛的,这直接导致了两种算法的差异。但单单从算法步骤上来讲,策略迭代算法旨在迭代无穷次贝尔曼方程(虽然现实中往往迭代有限次),从而得到准确的 \(V^\pi\),然后对策略进行更新;价值迭代算法,仅仅迭代了一次 \(V\),就对策略进行相应的更新。拿第一次策略更新 \(\pi_1\rightarrow \pi_2\) 时,二者对价值函数的计算为例:
在现实中,策略迭代算法往往因为对 \(V^\pi\) 的迭代次数过多,而导致求解时间过长;而在相同策略更新次数下,价值迭代算法往往收敛速度很慢(仅进行了一次 \(V^\pi\) 的迭代)。为了结合二者的优劣,可以采取一种截断式方式:
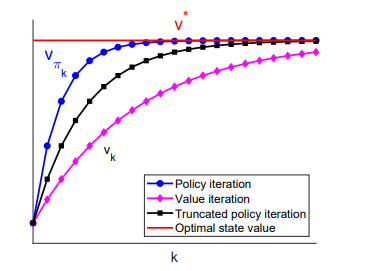
由于截断策略迭代算法是介于策略迭代和价值迭代之间,因此容易证明其收敛性,在相同策略更新次数下,三种算法收敛状况如下: