「赛后总结」20230727 CSP 模拟赛
2023 年 7 月 28 日 20:04:早上就写完了但忘了发了。以下内容均写于「2023 年 7 月 27 日」。
前两天题还没改完呢,有空补上。
情商有待提高。
破防了,今天看啥感觉都在 D 我。



听说了 NOI 2023 现状,金牌线 509,银牌线 400+,太恐怖了。据说算上牛子 HZOI 一共就两个 Ag,还有打铁的。然而南方各省一车 Au 甚至高一 Au。
不同省省队实力差距相当大,放到一个地方比赛比个锤子啊。要不退役了吧,HE 搞 OI 没前途。
但是只是嘴上说说,真放下太困难了。
APJ 好像挺崩溃,想安慰安慰但我不太会安慰人,还是不说什么了。
看了看我模拟赛排名,T2 T3 不挂分也是 rk7,校内考成这破样,放南方真有什么竞争力吗。
很压抑,很恐惧,不敢想等到我上场后会寄成什么玩意。但是看着身边好像就没什么人对这件事感觉很大,仔细思考可能是我自己目标太高了,那还是别给自己太大压力了,注意精神状态。
冲个 p Au,先看看自己能不能冲 Ag 吧。
场外吃瓜都能这么影响精神状态,那我在赛场上会有一个什么样的精神状态呢。
今日乐子:

然后 ▇▇▇▇ 成功被线下 ▇▇。
总结
T1 取模后还取最大值,消愁了,寄。
T2 \(\dbinom{n}{m}\) 没判是否 \(n\ge m\),挂 30,寄。
T3 负下标 RE,挂 30,寄。
T4 不会,寄。
寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄寄。
题解
T1 卷
比较对数,这样不会被取模影响。
记住这句话:
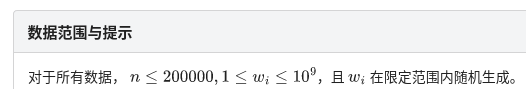
然后:


好厉害的随机化算法!
点击查看代码
const ll N = 2e5 + 10, P = 1e9 + 7;
namespace SOLVE {
ll n, w[N], f[N][2], ans;
ldb lg[N], g[N][2];
std::vector <ll> tu[N];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline void DFS (ll u, ll fa) {
f[u][0] = 1, f[u][1] = w[u];
g[u][0] = log (1), g[u][1] = log (w[u]);
far (v, tu[u]) {
if (v == fa) continue;
DFS (v, u);
if (g[v][1] > g[v][0]) g[u][0] = g[u][0] + g[v][1], f[u][0] = f[u][0] * f[v][1] % P;
else g[u][0] = g[u][0] + g[v][0], f[u][0] = f[u][0] * f[v][0] % P;
g[u][1] = g[u][1] + g[v][0], f[u][1] = f[u][1] * f[v][0] % P;
}
return;
}
inline void In () {
n = rnt ();
_for (i, 1, n) w[i] = rnt ();
_for (i, 1, n - 1) {
ll u = rnt (), v = rnt ();
tu[u].push_back (v);
tu[v].push_back (u);
}
return;
}
inline void Solve () {
DFS (1, 0);
return;
}
inline void Out () {
printf ("%lld\n", g[1][0] > g[1][1] ? f[1][0] : f[1][1]);
return;
}
}
T2 简单题
可以将 \(n\) 个数分成若干个 \(\{2^0a, 2^1a, \cdots, 2^ka\}\) 形式的集合。其中 \(a\) 为奇数,\(2^ka\) 小于 \(n\)。
观察题面,发现我们只要在每个集合里面交替取数即可。设一个集合大小为 \(x\),若 \(x\) 为偶数则其贡献一定为 \(\frac{x}{2}\),有两种选法,否则至少产生 \(\left\lfloor\frac{x - 1}{2}\right\rfloor\) 的贡献,换种选法可以多获得 \(1\) 的贡献。
查询 \(m\) 时考虑先减去基础贡献,令 \(m'\) 等于 \(m\) 减去大小为偶的集合贡献和大小为奇的集合最少的贡献,答案算上大小为偶的集合选取方案数,再计算大小为奇的集合里选出 \(m'\) 个数的方案数。
考虑快速求出集合。发现集合贡献和集合每个数没关系,而且只知道首项即可知道每一项,就是不断左移。考虑想成二进制处理。
据说不加 Lucas 能过,疑惑。
点击查看代码
const ll N = 1e5 + 10, P = 1e7 + 19;
namespace SOLVE {
ll n, q, num, cnt[2][2], fac[P], inv[P];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline ll FastPow (ll a, ll b) {
ll ans = 1;
while (b) {
if (b & 1) ans = ans * a % P;
a = a * a % P, b >>= 1;
}
return ans;
}
inline ll C (ll n, ll m) {
if (n < m) return 0;
return fac[n] * inv[n - m] % P * inv[m] % P;
}
inline ll Lucas (ll n, ll m) {
if (!n) return 1;
return Lucas (n / P, m / P) * C (n % P, m % P) % P;
}
inline void In () {
n = rnt (), q = rnt ();
return;
}
inline void Solve () {
ll tmp = n, la = n, p = 0;
while (tmp) {
++p, tmp >>= 1;
cnt[0][p & 1] += (la - tmp) / 2 + ((la & 1) && !(tmp & 1));
cnt[1][p & 1] += ((la - tmp) / 2 + ((la & 1) && !(tmp & 1))) * p;
la = tmp;
}
num = FastPow (2, cnt[0][0]);
fac[0] = 1;
_for (i, 1, P - 1) fac[i] = fac[i - 1] * i % P;
inv[P - 1] = FastPow (fac[P - 1], P - 2);
for_ (i, P - 2, 0) inv[i] = inv[i + 1] * (i + 1) % P;
return;
}
inline void Out () {
_for (i, 1, q) {
ll m = rnt ();
m = m - cnt[1][0] / 2 - (cnt[1][1] + cnt[0][1]) / 2 + cnt[0][1];
if (m < 0 || m > cnt[0][1]) puts ("0");
else printf ("%lld\n", num * Lucas (cnt[0][1], m) % P);
}
return;
}
}
T3 粉丝
Rolling_star 说这个和南昌起义的 E 题比较像,疑惑半天发现他说的其实是义,确实很像啊。
暂时不考虑 \(x\) 和 \(y\) 的限制。
考虑根号分治。
对于小于 \(\sqrt{n}\) 的数,考虑使用背包。
对于大于等于 \(\sqrt{n}\) 的数,我们设 \(g_{i, j}\) 表示当前分成了 \(i\) 个数字,总和为 \(j\)。转移思路和义的 \(g\) 一模一样,懒得写了。
然后考虑限制,使用容斥,答案是限制大于等于 \(x\) 的方案数减去限制大于等于 \(y + 1\) 的方案数。
对于一个限制大于等于 \(k\),我们控制小于 \(\sqrt{n}\) 的数从 \(k\) 开始遍历,大于等于 \(\sqrt{n}\) 的数至少加 \(k\) 次 \(1\)。
点击查看代码
const ll N = 1e5 + 10;
namespace SOLVE {
ll x, y, n, P, sq, f[N], g[N], _g[N], ans;
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline ll Calc (ll limit) {
memset (f, 0, sizeof (f));
memset (g, 0, sizeof (g));
memset (_g, 0, sizeof (_g));
ll b = std::max (sq, limit);
f[0] = g[0] = _g[0] = 1;
_for (i, limit, b - 1) _for (j, i, n) f[j] = (f[j] + f[j - i]) % P;
_for (i, 1, n / sq) {
ll p = b * i;
_for (j, i, n - p) g[j] = (g[j] + g[j - i]) % P;
_for (j, 0, n - p) _g[j + p] = (_g[j + p] + g[j]) % P;
}
ll sum = 0;
_for (i, 0, n) sum = (sum + f[i] * _g[n - i] % P) % P;
return sum;
}
inline void In () {
x = rnt (), y = rnt (), n = rnt (), P = rnt ();
return;
}
inline void Solve () {
sq = std::sqrt (n);
ans = (Calc (x) - ((y == n) ? 0 : Calc (y + 1)) + P) % P;
return;
}
inline void Out () {
printf ("%lld\n", ans);
return;
}
}
T4 字符串

会马拉车一周年了,然后又给我一个马拉车题。
考虑先删去两边相同的,这样一定会删完 \(A\) 或者 \(E\),我们设剩下的四部分为 \(A, B, C, D\),\(B+D\) 在整个序列翻转后成为 \(A+C\),所以只考虑 \(A + C\) 的情况,之后 reverse 一下再算一次即可。
观察,发现这个 \(C\) 是一个回文串加上一个翻转的 \(A\),考虑使用 Manacher 求出回文半径,然后枚举回文中心,现在要解决的是如何快速找到一个回文串后面的子串,与翻转的前缀相同且最长。
把序列翻转过来放在原序列后面,倒着跑 KMP,一个例子是:
b a b a b b b a a # a a b b b a b a b
5 4 3 2 1 1 1 0 0 0 0 2 1 1 3 2 1 0 0
这时 \(nxt_i\) 的含义是:以 \(i\) 开头的翻转后是原字符串前缀的字串的最长长度。
这不就解决了。
点击查看代码
const ll N = 5e6 + 10;
namespace SOLVE {
ll n, m, d[N * 2], nxt[N * 2], mx[N * 2], ans;
char s[N], t[N * 2];
inline ll rnt () {
ll x = 0, w = 1; char c = getchar ();
while (!isdigit (c)) { if (c == '-') w = -1; c = getchar (); }
while (isdigit (c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar ();
return x * w;
}
inline void Manacher () {
t[1] = '#', m = 2 * n + 1;
ll l = 0, r = -1;
_for (i, 1, n) t[i * 2] = s[i], t[i * 2 + 1] = '#';
_for (i, 1, m) {
ll k = (i > r) ? 1 : std::min (d[r + l - i], r - i + 1);
while (i - k && i + k <= m && t[i - k] == t[i + k]) ++k;
d[i] = k;
if (i + k > r) r = i + k, l = i - k;
}
return;
}
inline void KMP () {
t[n + 1] = '#';
_for (i, 1, n) t[n - i + 1] = t[n + i + 1] = s[n - i + 1];
memset (nxt, 0, sizeof (nxt)), memset (mx, 0, sizeof (mx));
ll j = 0;
for_ (i, m - 1, 1) {
while (j && t[i] != t[m - j]) j = nxt[j];
j += (t[i] == t[m - j]), nxt[i] = j;
}
for_ (i, n, 1) mx[i] = std::max (mx[i + 1], nxt[i]);
return;
}
inline void GetAns () {
Manacher (), KMP ();
_for (i, 1, m) {
ll l = (i - d[i]) / 2, r = (i + d[i]) / 2;
if (nxt[r] <= l) ans = std::max (ans, d[i] + 2 * nxt[r] - 1);
if (mx[r] >= l) ans = std::max (ans, d[i] + 2 * l - 1);
}
return;
}
inline void In () {
scanf ("%s", s + 1);
n = strlen (s + 1);
return;
}
inline void Solve () {
ll k = 0;
while (k <= (n + 1) / 2 && s[k] == s[n - k + 1]) ++k;
--k, n -= 2 * k;
_for (i, 1, n) s[i] = s[i + k];
s[n + 1] = '\0';
GetAns ();
std::reverse (s + 1, s + n + 1);
GetAns ();
ans += 2 * k;
return;
}
inline void Out () {
printf ("%lld\n", ans);
return;
}
}