摘要:
目标导向的路径规划在移动机器人领域是基础且被广泛研究。由于障碍物的存在而产生的同一类轨迹,被定义为可以通过逐渐弯曲和拉伸而在不与障碍物碰撞的情况下相互转换的轨迹集合。在诸如预测动态实体的路径和计算具有动态约束的路径规划的启发式算之类的应用中,频繁出现寻找限制于特定通论类的最小代价路径或寻找不属于特定同论类的最小代价路径问题。在先前的工作中,我们研发了一种表示同论类的紧凑方法并提出了一种基于图搜索的具有同论类约束的最优路径规划的有效方法。该方法基于将机器人的环境表示为复杂平面,并利用柯西积分定理。我们证明了该方法的最优性,并通过实验证明了其有效性。
介绍:机器人路径规划算法可能是机器人学中研究最广泛的问题之一。尽管对具有各种约束的路径规划进行了广泛的研究,如通信约束(Abichandani、Benson和Kam 2009)、动力学和环境约束(Likhachev和Ferguson 2008)和时间约束(Hansen和Zhou 2007),但对具有同源约束的路径规划的研究却很少(Grig-oriev和Slissenko 1998;Schmitzberger等人2002)
由连接相同起点和终点的轨迹集定义了一类同伦轨迹,这些轨迹可以在没有相交障碍物的情况下平滑地变形为彼此。由于环境中存在障碍物,产生了多个同论类。同伦类约束包括将解限制在某些允许的同论类或者禁止其他同伦类。
尽管这主要是一个未知的研究领域,在路径规划问题中经常出现同伦类的约束。例如,在多智能体规划问题中(Zhang,Kumar,and Ostrowski 1998;Karabakal和Bean 1995),轨迹通常需要满足某些邻近性或资源约束或者由于分配给智能体的任务而产生的约束,这转化为将解轨迹限制在某些同伦类。在探索和建图问题中(Bourgault等人,2002),智能体通常需要根据他们的任务或者分配给他们建图或者探索的环境进行路径规划,因此将他们的轨迹限制在某些同伦类中。
过去已经使用几何方法(Grigoriev和Slissenko 1998;Hershberger和Snoeyink 1991)和概率路线图构建技术研究了具有同伦类的运动规划。这种技术具有表示同伦类的复杂性,并且不能立即与标准的图搜索技术整合在一起。例如(Grigoriev and Slissenko 1998)通过基于轨迹与障碍物的切割的相交数量形成一个词,从而减少该词来描述同伦类。虽然使用这种技术可以比较不同同伦类中的轨迹并在环境中找到不同的同伦类,但具有同伦类约束的最优路径规划无法以有效的方式实现。
在基于三角测量的路径规划(Demyen和Buro 2006)技术中,通过连接多边形的顶点来创建三角形图,首先将具有多边形障碍物的环境分解为三角形。这个图可以简化为一个抽象的三角形图,其中的路径可以表示环境中的各种同伦类。然后,可以在图(TRA*)中执行A*搜索的修改版本,以获得三角形通道,从中可以使用漏斗算法(Kallmann 2005)导出成本最低的路径。然而,三角测量图的构建依赖于这样的假设,即环境中的障碍物是多边形的,或者至少可以近似为多边形。在实际场景中,例如,当由机器人上的传感器构建时,环境通常包含形状奇怪的小障碍物和噪音。小障碍物的存在可能会产生许多薄三角形。为了保证无碰撞路径,需要考虑每个不相交的障碍来构造抽象简化图。因此,它们有助于大量的同伦类,而我们通常只需要考虑定义同伦类的几个大障碍。此外,基于三角测量的路径规划中的代价函数被限制为轨迹的欧几里得长度。
在本文中,我们提出了一种表示轨迹的同伦类的紧凑方法,该方法与几何、离散化、代价函数或者搜索算法无关。我们的方法基于复数分析,并利用柯西积分定理来刻画同伦类。我们证明了这种表示可以无缝地编织到任意离散化环境中的标准图搜索技术中,并施加所需的同伦类约束。需要注意的是,我们提出的方法与环境的离散化方案、需要优化的代价函数的性质或使用的搜索算法无关。因此,这种方法可以被纳入许多现有的规划器中,使他们能够施加同伦类约束。此外,如果某些障碍物的大小太小,我们可以选择不包括他们来创建同伦类。我们已经用网格离散化和可见性图在不同大小的不同环境中演示了我们的算法。我们的实验结果证明了该方法的有效性、可扩展性和适用性。
复分析
在这一节中,我们简要回顾了复分析的一些基本定理(Gamelin 2001)。
The Cauchy Integral Theorem:柯西积分定理指出如果f:C→ C是某个单连通区域R中的全纯(解析)函数,γ是完全包含在R中的闭定向(即有向)轮廓,则以下成立:
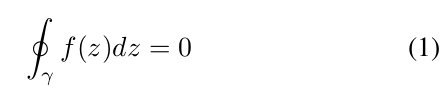
并且,此外,如果z0是由γ包围的区域内的一个点,该点具有逆时针(或正)方向,并且F(z)=F(z)/(z−z0)在z0处具有极点,则以下成立
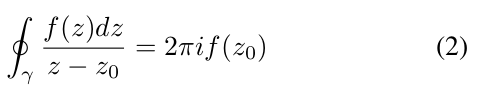
The Residue Theorem(剩余定理):柯西积分定理的一个直接结果,剩余定理,指出,如果F:R→ C是一个定义在一些单连通区域R⊆C中的函数,它在不同的点a1,a2,···,aM∈R上有单极点,并且在R中的其他所有地方都是全纯的(解析的),并且假设γ是一条完全包含在R中并且只包含F极点中的点ak1,ak1,··,akm的闭合正向Jordan曲线,则以下成立:
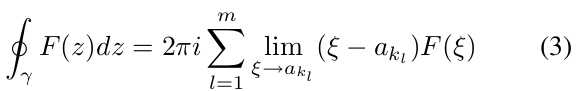
该场景如图1(b)所示。
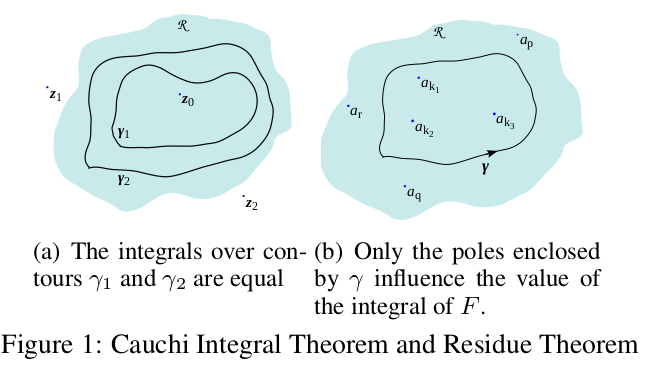
(a)γ1和γ2上的积分是相等的(b) 只有被γ包围的极点会影响F的积分值。值得注意的是,在柯西积分定理和残差定理中,只要满足上述条件,积分的值就与轮廓γ的精确选择无关(见图1(a))。
同构类的表示
定义1(轨迹的同构类)。τ1和τ2这两条轨迹(或路径)被认为是同一同构类,当其中一条轨迹可以平滑变形为另一条轨迹时,不会有相交的障碍物。否则,它们属于不同的同构类。我们用复平面C表示机器人的二维配置空间。
假设障碍物是C中的单连通区域,并用O1,O2,··,ON表示。我们为每个相连的障碍物定义一个“代表点”,使它们位于各自障碍物的内部。因此我们定义了点ζi∈O i,∀i=1,··,N。图2(a)显示了三个障碍物内的这些代表点。

(a)在同一同源类中,形成闭合轮廓 (b)在不同的同源类中,封闭障碍
正如我们稍后将要讨论的那样,我们没有必要为所有障碍选择具有代表性的观点。我们只需要在更大的相关障碍上选择这样的点,这些障碍有助于实现同伦类的实用概念。较小的障碍可以忽略不计。
定义2 (障碍物标记函数):对于给定的一组“代表点”,我们定义“障碍标记函数”函数F如下:,
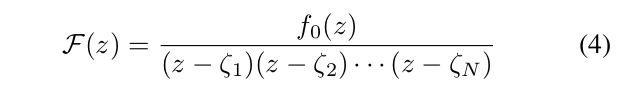
其中f0是整个C上的任何解析函数。
此外,我们定义了∀i=1,···,N,
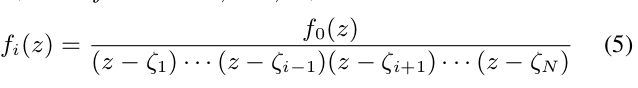
因此,f i(z)=(z−ζi)f(z)在不包含ζ1、··、ζi−1、ζi+1、···、ξN但可以包含ζi的区域内是解析的。
假设1:我们注意到,对于给定的一组障碍,我们在选择障碍内部的“代表点”和函数f0时有很大的自由度。
我们假设ζ1,ζ2,···,ζN和f0的选择满足
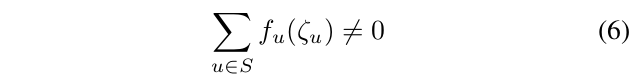
对于任意的S属于S ⊆ {1, 2, · · · , N }。虽然很明显,在一般情况下,这个条件不太可能被违反,但我们仍然可以通过检查每个s的所选ζi’s和f0来强制执行这些条件。在(6)不满足的不太可能的情况下,我们简单地选择不同的ζi’s和f0。
引理1:如果连接相同点的两个轨迹τ1和τ2位于同一个同伦类中,则以下成立,

证明:我们注意到,通过改变执行积分的路径的方向,我们改变了积分的符号。如果τ是一条路径,则其反向路径表示为-τ。因此,正如我们从图2(a)中看到的那样,τ1和-τ2形成了一个正取向的闭环。
此外,由于τ1和τ2位于同一个同伦类中,τ1和σ2包围的区域不包含任何“代表点”ζi,因此使函数F在该区域中具有解析性。因此,从柯西积分定理我们得到,

引理2:
如果连接相同点的两个轨迹τ1和τ2位于不同的同伦类中,则以下成立,
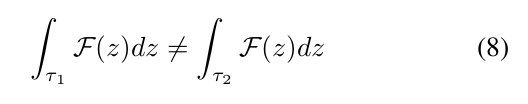
证明:如果τ1和τ2在不同的同伦类中,我们可以很容易地注意到,由τ1和-τ2形成的闭合正轮廓将包围一个或多个障碍物,并因此包围它们相应的“代表点”。如图2(b)所示。让我们假设封闭的“代表点”是ζκ1、ζκ2、··、ζ·n。此外,我们注意到函数F在ζ1、ζ2、··、ζN处只有简单的极点。因此根据剩余定理和定义2:

引理1和2一起暗示,在给定的环境中,我们可以通过障碍标记函数沿轨迹的线积分值来识别轨迹的同伦类。为了便于表示给定轨迹τ,我们写

称之为轨迹τ的L值。
因此,引理3:同一个同伦类中的轨迹(连接相同的两点)的L值相等,而不同同伦类的轨迹的L值不同。