posted on 2022-10-08 22:03:07 | under 题解 | source
神仙 min-cut,果然,flow 题的难点是想到 flow,非 flow 题的难点是不要想到 flow。
problem
平面直角坐标系上 \(n\) 个整点带权,删除一些点,使得不存在四个点 \(v,v_1,v_2,v_3\) 满足:
- \(v\) 的横纵坐标均为偶数;
- \(v\) 与 \(v_1,v_2,v_3\) 的切比雪夫距离(两维距离之差最大值) \(dist(v,v_1)=1,dist(v,v_2)=1,dist(v,v_3)=1\);
- \(v,v_1,v_2,v_3\) 四点组成的平行四边形(或正方形)有一边与 \(x\) 轴平行。
求删除的点的最小权值和。\(n\leq 10^3\)。
solution
- 将整点按照横纵坐标奇偶性分四类,则 \(v,v_1,v_2,v_3\) 中各含有一类点;
- 发现 \((odd,even)\to(even,even)\to(even,odd)\to(odd,odd)\) 与题述四边形一一对应。
- 建立最小割模型,随便搞一下即可。将点按照奇偶分为四列排成四排,按照 \((odd,even)\to(even,even)\to(even,odd)\to(odd,odd)\) 连接无穷大的边,同时每个点拆成入点和出点,中间连上自己的权值。
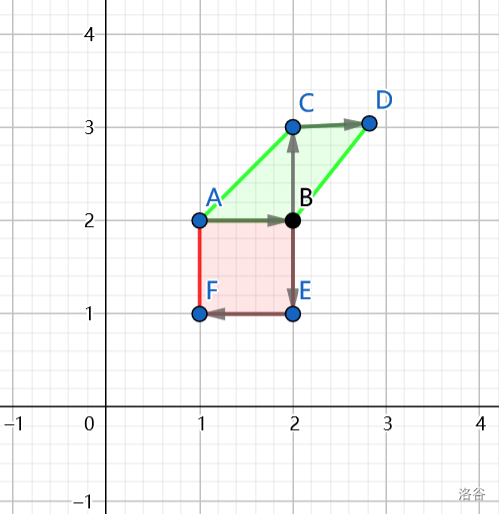
不难发现这个东西对,但它是怎么想出来的呢?第一是要知道奇偶分类,考虑刻画路径(不要搞成环)转化为最小割。第二,考虑到与 \(x\) 轴平行的条件,那么 \((0,0),(1,0)\) 和 \((1,1),(0,1)\) 这两对必须相邻。第四,确定了平行于 \(x\) 轴的两边之后,要考虑中间怎么连。如果中间连了条斜线,有可能两端直接跨出去了,不满足条件。剩下的合法路径大概只有 \(10\to00\to01\to11,00\to10\to11\to01\) 以及它们的翻转等各种形态。
code
#include <queue>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
typedef long long LL;
template<int N,int M,class T=int> struct graph{
int head[N+10],nxt[M*2+10],cnt,tot;
struct edge{
int u,v;T w;
edge(int u=0,int v=0,T w=0):u(u),v(v),w(w){}
} e[M*2+10];
graph(){memset(head,tot=cnt=0,sizeof head);}
edge& operator[](int i){return e[i];}
void add(int u,int v,T w=0){e[++cnt]=edge(u,v,w),nxt[cnt]=head[u],head[u]=cnt;}
void link(int u,int v,T w=0){add(u,v,w),add(v,u,w);}
};
template<int N,int M,class T=int> struct maxflow:public graph<N,M,T>{
graph<N,M,T> &g=*this;
int cur[N+10],dep[N+10]; bool vis[N+10];
maxflow(){g.add(0,0,0);}
int insert(int u,int v,T w){return g.add(u,v,w),g.add(v,u,0),g.cnt-1;}
bool bfs(int s,int t){
queue<int> q;
memset(dep,0,sizeof dep);
memcpy(cur,g.head,sizeof cur);
for(q.push(s),dep[s]=1;!q.empty();){
int u=q.front();q.pop();
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!g[i].w||dep[v]) continue;
q.push(v),dep[v]=dep[u]+1;
}
}
return dep[t];
}
T dfs(int u,T flow,int t){
if(u==t||!flow) return flow;
T rest=flow;
for(int &i=cur[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!g[i].w||dep[v]!=dep[u]+1) continue;
if(T ans=dfs(v,min(rest,g[i].w),t)){
g[i].w-=ans,g[i^1].w+=ans;
rest-=ans;
if(!rest) break;
}
}
if(flow==rest) dep[u]=0;
return flow-rest;
}
T dinic(int s,int t,T inf=1e9){
T flow=0;
while(bfs(s,t)) flow+=dfs(s,inf,t);
return flow;
}
};
//template<int N,int M,class T=int> struct maxflow:graph<N,M,T>{
// graph<N,M,T> &g=*this;
// maxflow(){g.add(0,0);}
// void insert(int u,int v,T w){g.add(u,v,w),g.add(v,u,0);}
// int dis[N+10],hbf[N+10];
// bool bfs(int s,int t){
// queue<int> q;
// memset(dis,0x3f,sizeof dis);
// for(q.push(s),dis[s]=0;!q.empty();){
// int u=q.front();q.pop();
// for(int i=g.head[u];i;i=g.nxt[i]){
// int v=g[i].v;
// if(g[i].w&&dis[v]>dis[u]+1){
// dis[v]=dis[u]+1;
// q.push(v);
// }
// }
// }
// return dis[t]<1e9;
// }
// T dfs(int u,int t,T flow){
// if(u==t||!flow) return flow;
// T rest=flow;
// for(int &i=g.head[u];i;i=g.nxt[i]){
// int v=g[i].v;
// if(dis[u]+1!=dis[v]||!g[i].w) continue;
// if(T res=dfs(v,t,min(rest,g[i].w))){
// g[i].w-=res;
// g[i^1].w+=res;
// rest-=res;
// if(!rest) break;
// }
// }
// if(flow==rest) dis[u]=1e9;
// return flow-rest;
// }
// T dinic(int s,int t,T inf=1e9){
// T flow=0;
// memcpy(hbf,g.head,sizeof hbf);
// while(memcpy(g.head,hbf,sizeof hbf),bfs(s,t)){
// while(T f=dinic(s,t,inf)) flow+=f;
// }
// return flow;
// }
//};
int n,x[20010],y[20010],typ[20010],inn[20010],out[20010],S,T;
int dist(int i,int j){return max(abs(x[i]-x[j]),abs(y[i]-y[j]));}
maxflow<40010,400010,LL> g;
LL sum;
int main(){
scanf("%d",&n);
for(int i=1,v;i<=n;i++){
scanf("%d%d%d",&x[i],&y[i],&v);
inn[i]=++g.tot,out[i]=++g.tot;
g.insert(inn[i],out[i],v);
typ[i]=(x[i]&1)<<4|(y[i]&1);
sum+=v;
}
S=++g.tot,T=++g.tot;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(dist(i,j)!=1) continue;
if(typ[i]==0x10&&typ[j]==0x00) g.insert(out[i],inn[j],1e18);
if(typ[i]==0x00&&typ[j]==0x01) g.insert(out[i],inn[j],1e18);
if(typ[i]==0x01&&typ[j]==0x11) g.insert(out[i],inn[j],1e18);
}
}
for(int i=1;i<=n;i++) if(typ[i]==0x10) g.insert(S,inn[i],1e18);
for(int i=1;i<=n;i++) if(typ[i]==0x11) g.insert(out[i],T,1e18);
printf("%lld\n",sum-g.dinic(S,T,1e18));
return 0;
}
review
并没有想到这个路径表示图形的方法。。。
扩展:平行于 \(y\) 轴:\((even,odd)\to(even,even)\to(odd,even)\to(odd,odd)\)。
T dinic(int s,int t,T inf=1e9){
T flow=0;
memcpy(hbf,g.head,sizeof hbf);
while(memcpy(g.head,hbf,sizeof hbf),bfs(s,t)){
while(T f=dinic(s,t,inf)) flow+=f;
// ^~~~~
}
return flow;
}