ARC063F
白色区域一定是一个矩形。
假设我们已经知道了矩形的两个分界线
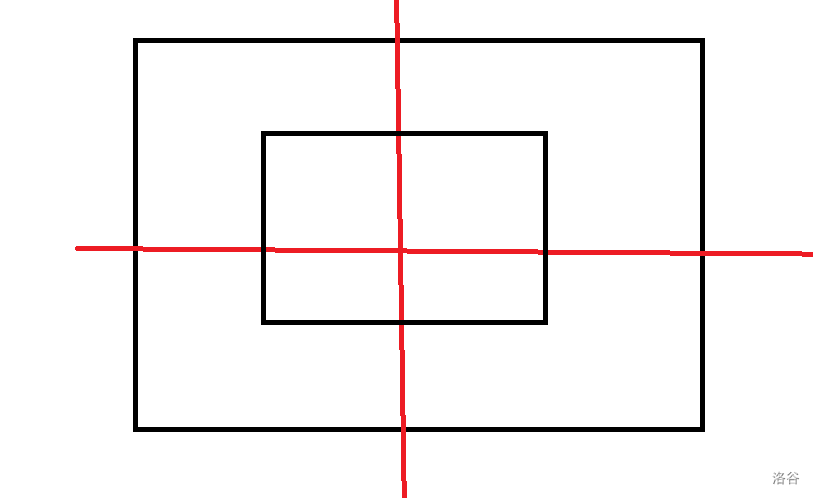
考虑所有跨过两条红色线的矩形。
在确定了两条分界线后,矩形的四个顶点所在区域就确定了。
考虑暴力枚举矩形的左右边界,那么上下边界就跟着确定了:
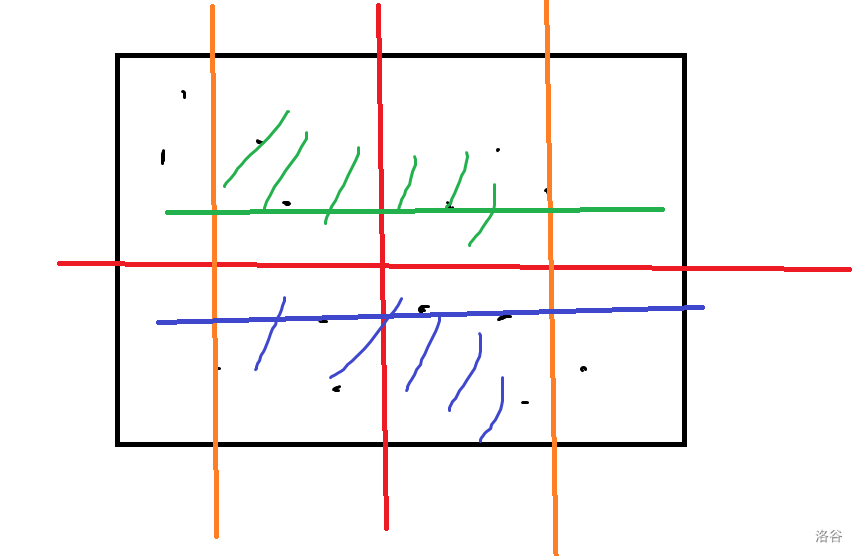
上边界即为上半区域(图中绿色)中最下面的点确定的横线,下边界为下半区域(图中蓝色)的最上面的点确定的横线。
我们预处理出每个横坐标到中间分界线之间上半区域点纵坐标最小值和下半区域纵坐标最大值,记为 \(Mn_i,Mx_i\),这样暴力枚举后直接取两个横坐标对应的 \(Mx,Mn\) 合并即可。
现在我们只枚举左边界,考虑右边界往右移动的过程中上下边界的变化。
右边界往右移动过程中有一段区域上下边界与左边所确定的上下边界一致,不变化,接着有一段区域上下边界的其中一个发生变化,另一个保持不变,最后一段区域上下边界都在变化。
考虑对三段区域分别求出周长的最大值。
- 第一段由于上下边界不变,显然直接取最右边的点就行了。
- 第二段上下边界中的一个在变,假设是上边界在变,设左边确定的左边界为 \(x_1\),下边界为 \(y_1\),那么对于右边界 \(x\),若它对应的上边界为 \(y\),对应的周长为 \(2(x-x_1+y-y_1)\),于是需要维护区间 \(x+y\) 的最大值,用
ST表即可,下边界在变同理。 - 第三段上下边界都在变化,假设右边界 \(x\) 对应的上下边界为 \(y_1,y_2\),那么需要维护 \(x+y_1-y_2\) 的最大值,这个只需要预处理后缀max即可。
好像有点抽象,将就着看吧。
那么如果分治套分治去枚举两个分界线,复杂度为 \(\mathcal{O}(n\log^3n)\),应该过不去。
但是这个题还有一个性质:
最优长方形一定至少跨过两条中轴线的其中一个。
证明:通过把所有点往水平方向染色容易构造出周长至少为 \(2H+2\) 的矩形,通过把所有点往竖直方向染色容易构造出周长至少为 \(2W+2\) 的矩形,因此最优矩形周长至少为 \(2\max(H,W)+2\),而如果一个矩形两个中轴线都不跨过,周长最长为 \(H+W\),显然不优。
因此一定有一维跨过中轴线,以此为其中一个分界线,再分治枚举另一个分界线即可,复杂度 \(\mathcal{O}(n\log^2n)\)。