伯努利实验

伯努利实验概念及性质

定义：事件域为：\(\mathcal F = \{ \varnothing ,A,\bar A,\Omega \}\)，只两种可能结果的试验称为伯努利实验。
现考虑重复n次独立试验的伯努利实验（这里每个\(A\)概率不变），这种实验称之为n重伯努利实验，记为\(E^n\)。
其样本点形如：

\[(\hat A_1,\hat A_2,...,\hat A_n) \]

其中每个都有两种可能取值。易得样本点一共有\(2^n\)。概率空间易得不再赘述。

伯努利分布

伯努利分布（Bernoulli Distribution）是一种离散型概率分布，它用于描述只有两种结果（例如成功和失败）的随机试验。伯努利分布可以用一个参数\(p\)来描述成功的概率。概率分布可简单表示为：

\[P(X=k) = kp+(1-k)(1-p) \]

其中k仅有0，1两个取值。这样写概率的好处在于：可以用于最大似然估计中的求导。
伯努利分布的期望和方差分别为：

\[E(X)=p \cdot 1 + (1-p) \cdot 0=p \]

\[Var(X)=(EX)^2 -EX^2= p(1-p) \]

伯努利分布通常用于二元分类问题中，例如预测一个事件是否发生、一次抛硬币的结果等。

二项分布

如果有多次独立的伯努利试验，可以使用二项分布（Binomial Distribution）来描述（简记为B）。
若记\(B_k\)为n重伯努利实验中事件\(A\)正好出现\(k\)次。则：

\[P(B_k) = C_n^kp^kq^{n-k} \]

二项分布的重要性质

概率函数的形状：二项分布的概率函数呈现出类似钟形曲线的形状，当\(p=0.5\)时，概率函数的峰值达到最高。
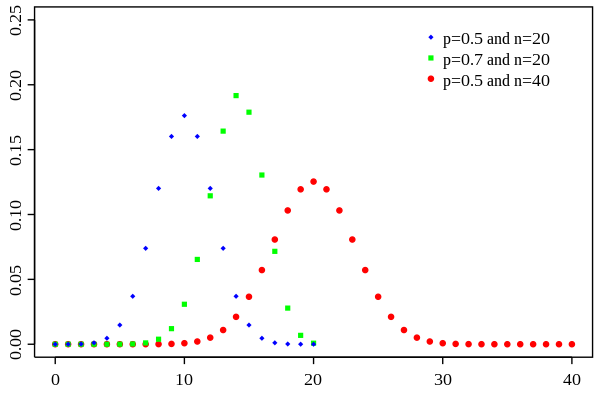
期望和方差：二项分布的期望和方差分别为\(E(X)=np\)和\(Var(X)=np(1-p)\)
由于每次试验独立，期望与方差可以简易地由伯努利分布的期望与方差推出。
若要依据其概率分布来推，则二项分布期望推导如下：

\[E(X) = \sum^n_{k=0}kP(B_k) = \sum^n_{k=0}kC_n^kp^k(1-p)^{n-k} \]

而

\[\sum^n_{k=0}kC_n^kp^k(1-p)^{n-k} =\sum^n_{k=0} \frac{kn!}{k!(n-k)!}p^k(1-p)^{n-k} \]

\[= np\sum^{n}_{k=1}\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{n-k} \]

上式右边部分是\(n-1\)次实验抽到\(k-1\)个的概率对k求和，从而为1。
二项分布的方差推导如下：

\[E(X^2) = k(k-1)\sum^n_{k=0}C_n^kp^k(1-p)^{n-k}+k\sum^n_{k=0}C_n^kp^k(1-p)^{n-k} \]

与上面求期望的同理，把\(k(k-1)\)乘进\(C\)的表达式即可。这个构造我认为非常有用，这样的话即便是\(E(X^3)\)，也可以拆成\(k(k-1)(k-2)+ak(k-1)+bk\)的形式进一步求解。回到原话题，由上易得

\[E(X^2) = n(n-1)p^2+np \]

从而最终得到\(Var(X)= np(1-p)\)

大数定律：二项分布具有大数定律，即当试验次数\(n\)趋近于无穷大时，二项分布的概率函数逐渐趋近于正态分布
中心极限定理：二项分布满足中心极限定理，即当试验次数\(n\)足够大时，二项分布可以近似看作正态分布

几何分布

现在讨论在伯努利实验中手册成功出现在第k次实验的概率。记第k次实验出现\(A\)的事件为\(W_k\)，有：

\[P(W_k)=q^{k-1}p \]

几何分布性质

无记忆性：几何分布具有无记忆性，即在已知前\(k\)次试验失败的情况下，下一次试验仍然是独立的伯努利试验，成功的概率仍然是\(p\)
概率函数的形状：几何分布的概率函数呈现出右偏斜的单峰形状，随着等待次数\(k\)的增加，概率逐渐减小
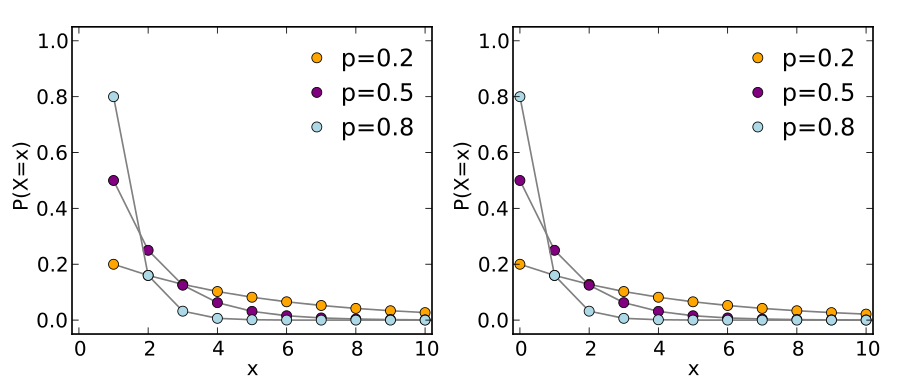
期望和方差：几何分布的期望为\(E(X)=\frac{1}{p}\)，方差为\(Var(X)=\frac{1-p}{p^2}\)
期望可由高中数列错位相减法处理，是比较易得的。方差稍微有些变化：

\[E(X^2)= \sum^{\infty}_{k=1}k^2pq^{k-1}=p(\sum^{\infty}_{k=1}kq^k)' \]

接下来的部分就不写了，总之容易得到\(Var(X)\)。

帕斯卡分布

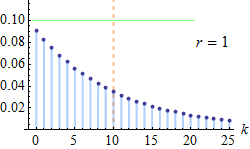
让我们以\(C_k\)表示第r次成功发生在第k次实验这一事件。

\[P(C_k) = C_{k-1}^{r-1}p^rq^{k-r} \]

这个概率分布被称之为帕斯卡分布。
典中典的就是分赌注问题。

帕斯卡分布与分赌注问题（Gambler's Ruin Problem）有着密切的联系。分赌注问题的确是一个比较正统的概率论问题，它也被看做是概率论诞生的事件。问题描述很简单，说甲乙两人下赌注，然后反复进行双人赌局，约定谁先赢\(?\)局者获胜。显然，有限赌局后一定可以分出胜负，有趣的问题是：赌局在甲胜\(r\)局、乙胜\(s\)局后被迫中止，那赌注该如何分配？一种最简单粗暴的方法就是按照\(r:s\)的比例关系分配，这种方法只是符合了含糊的直觉，完全经不起推敲。
但用帕斯卡分布的模型来看，就经得起推敲了。可从3个角度确定甲赢的概率：
（1）根据乙赢的次数或总次数；（2）根据乙赢时甲赢的次数；（3）接下来的\(m+n−1\)局里甲胜的局数。它们其实是相等的。依照概率分赌注，就会显得相当合理了。

随机游走

随机游走（Random Walk）是指在规定的状态空间中，按照一定的概率分布，随机地向某个方向前进的过程。随机游走可以在一维、二维或更高维的状态空间中进行。

在随机游走中，每一步的移动通常是独立的，且每一步的概率分布只依赖于当前的状态，与之前的状态或历史无关。在一维随机游走中，例如，每一步可以向左或向右移动一个单位距离，且向左或向右的概率相等，即\(p=0.5\)。在二维随机游走中，每一步可以向上、向下、向左或向右移动一个单位距离，且四个方向的概率相等，即\(p=0.25\)。

若质点可以在整个数轴的整数点上游动，则称这种随机游走为无限制随机游走。若在某点有个吸收壁，质点到这就不再动了，则称之为有吸收壁的随机游走。

无限制随机游走

《随机过程》教科书给出了一维简单随机游走随机变量的数学模型

\[S=X_1+X_2+...+X_n \]

易得\(E(S)=0,Var(S)=n\)
表明一维简单随机游走\(S_n\)的方差与步数\(n\)成正比，因此，一维简单随机游走是一个类似于物理学布朗运动的扩散过程。
方差是用来刻画随机变量偏离均值分散程度的数字特征，度量的是所有样本轨道（小球或醉汉）偏离均值的发散程度，因此，方差表明：随着步数n的增加，大量一维简单随机游走的小球会远离原点。

n次移动移动到k(k可以为负整数)的概率为：

\[P(R=k) = C_n^{\frac{n+k}{2}}q^{\frac{n-k}{2}}p^{\frac{n+k}{2}} \]

其中p为向上移动的概率，\(p+q=1\)（注意n、k必须同奇偶）。
来一些问题：