本博客主要参考书目为邱卫东的《密码协议基础》,本着知识共享的目的,博主自制了扫描版,下载地址

基本定义:

博主注:可信第三方(Trusted Third Party,TTP)

协议参与者诚实程度:

诚实参与者:

完全按照协议要求参与协议的执行.

半诚实参与者/被动攻击者/窃听者:

按照协议要求参与协议的执行,或者不参与协议(反正就是不提供非法输入),但会通过窃听方式获取自己不应知道的内容.

恶意攻击者:

拥有一个或多个伪装成参与者的"马甲",不仅窃听自己不应知道的内容,还会操控"马甲"提供非法输入以破坏协议的执行.

对于攻击者有更细致的分类:

静态攻击者:

在协议执行前,买通部分参与者作为自己的"马甲",协议开始后就不改变了.

动态攻击者:

协议执行过程中,通过协议的执行情况来决定买通哪些参与者作为"马甲".

移动攻击者:

比动态攻击者更强,被买通的"马甲"可随时转化为诚实参与者,诚实参与者也随时可能被买通变为它的"马甲".

攻击者能力:

无限计算能力:

在此类攻击下能保证安全的协议被称为信息论安全.

概念多项式计算能力(Probabilistic Polynomial Time,PPT):

在此类攻击下能保证安全的协议被称为密码学安全.

信道安全程度分类:

安全信道(secure channel):

诚实参与者之间的通信不会被窃听也不会被篡改.

非安全信道道(insecure channel)/认证的信道(authenticated channel):

诚实参与者之间的通信可能被窃听,但不会被篡改.

未认证的信道(unauthenticated channel):

完全被攻击者控制,通信会被窃听,也会被篡改.

博主注:这几个名字并不直观而且感觉怪怪的,在之后的表述中,博主会根据习惯将后两种信道称为可窃听信道与可篡改信道.

数学基础:

抽象代数:

一个算符的代数结构:

幺半群:

数的集合和一个算符构成的代数结构$(G,+)$,且满足

封闭性
结合律
存在单位元

群:

满足如下条件的代数结构$(G,+)$:

封闭性
结合律
存在单位元
对于每个元素均存在逆元

交换群/阿贝尔群:

满足如下条件的代数结构$(G,+)$.

封闭性
结合律
存在单位元
对于每个元素均存在逆元
交换律

两个算符的代数结构:

环:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

$(G,+)$是一个交换群
$(G,\cdot)$是一个幺半群
$\cdot$对$+$满足分配律

在环中,加法的单位元记为$0$,也称零元,乘法的单位元记为$e$或$1$

要求$(G,\cdot)$是幺半群而非群的理由是,$0$元素无法存在对$\cdot$的逆元

交换环:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

$(G,+)$是一个交换群
$(G,\cdot)$是一个满足交换律的幺半群
$\cdot$对$+$满足分配律

域:

数的集合和两个算符构成的代数结构$(G,+,\cdot)$,且

$(G,+)$是一个交换群
$(G,\cdot)$是一个满足交换律的幺半群
$\cdot$对$+$满足分配律
$R \backslash \{0\}$对$\cdot$存在逆元

大佬博客上的一张图能直观说明这几个概念之间的联系:

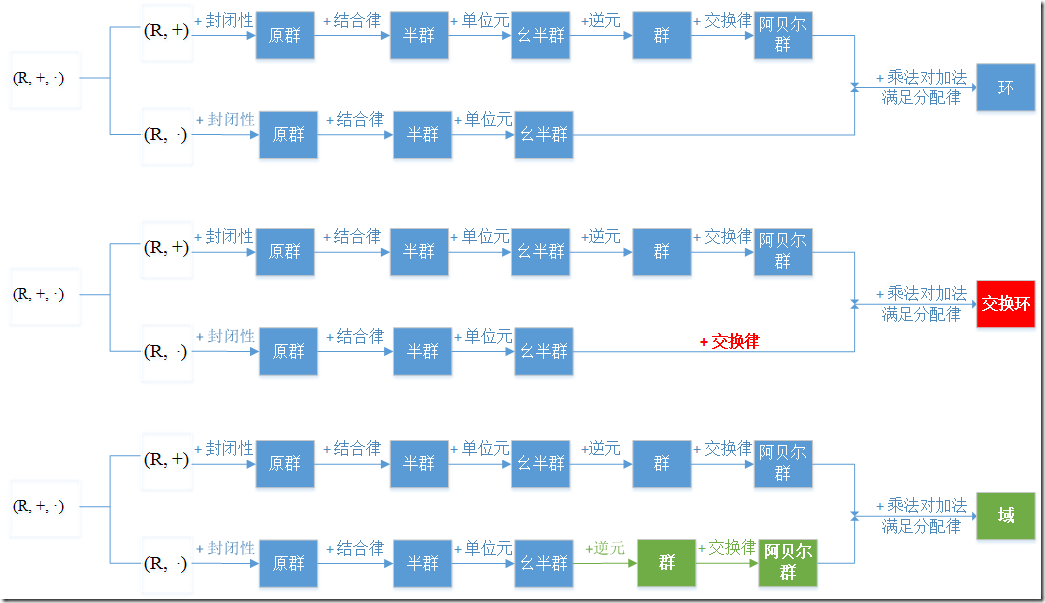
图源:http://sparkandshine.net/algebraic-structure-primer-group-ring-field-vector-space/

其他概念:

阶:

群,环,域等代数结构中,$R$的大小$|R|$.

循环群,循环子群,生成元:

设$(G,\cdot)$是群(一般讨论生成元时指的都是乘法群),$a\in G$,记 $(a)=\{a^i| i \in Z\}$,可以证明,$((a),\cdot)$为$(G,\cdot)$的子群,称$(a)$为由$a$生成的循环子群,并称$a$为该循环子群的生成元.

设$(G,\cdot)$是群,$a\in G$,若$a^n=e$,则对于那个最小的$n$,称$a$的阶为$n$.

可以证明,生成元的阶等于该生成元生成的循环子群的阶.

若群$(G,\cdot)$中存在元素$a\in G$,其生成的循环子群$(a)$就是$G$本身,那么称这个群为循环群,$a$为该群的生成元.

可以证明,阶数相同的所有循环群相互之间均同构.

数论:

欧拉定理:

欧拉函数:

记为$\phi(n)$,是$[1,n-1]$之间与$n$的最大公约数为$1$的数的个数.

可以证明,若$n=a_1^{x_1}\cdot a_2^{x_2} \cdots $,其中$a_1,a_2,\cdots$为$n$的质因数,那么$\phi(n)=(a_1-1)\cdot a_1^{x_1-1} \cdot (a_2-1)\cdot a_2^{x_2-1} \cdos$

例如,$100=2^2\cdot 5^2$,那么$\phi(100)=(2-1) \cdot 2^{2-1} \cdot (5-1) \cdot 5^{2-1}=40$,实际上,$[1,99]$中与$100$最大公约数为$1$的数有$1,3,7,9,11,13,17,19,21,23,27,29,31,33,37,39,41,43,47,49,51,53,57,59,61,63,67,69,71,73,77,79,81,83,87,89,91,93,97,99$,共计$40$个.

欧拉定理:

若$a,n$互质,则$a^{\phi(n)}=1 \mod n$

费马小定理:

首先不难看出,若$n$为质数,则$\phi(n)=n-1$

费马小定理本质上是欧拉定理的特殊形式,其形式为,若$n$为质数,那么任意$a\in[1,n-1]$,$a^{n-1}=1 \mod 1$,因此可以记$a^{n-2}=a^{-1} \mod n$,结合快速幂算法,这是一个计算模素数域的乘法逆元的简便方法.

原根:

阶:

回到欧拉定理,若$a,n$互质,则$a^{\phi(n)}=1 \mod n$,可将$\phi(n)$看作一个"循环节",但这个循环节并非最小循环节,例如,考虑$a=2,n=7$的情况,$\phi(7)=6$,固然有$2^6=1 \mod 7$,但实际上,$2^3=1 \mod 7$,$3$才是$2$在模$7$下的"最小循环节",称$2$在模$7$意义下的阶为$3$.写作$\mathrm{ord}_7(2)=3$.