前言

红黑树是一种性能非常优秀的有序数据结构，一般用于在内存中实现有序列表 / 集合 / 字典 / 优先队列等，在各大语言的标准函数库，操作系统中的任务调度、定时器等场景下有着广泛的应用。然而，红黑树也是一种以复杂闻名的数据结构，实现时需要考虑的情况非常之多，以至于“手撕红黑树”已经成为了面试官故意为难候选人的经典代名词。有感于此，笔者在学习过程中对各种情况加以总结，最终找到一条自认为较为清晰的理解思路，在此写成文章和大家分享。这篇文章将尝试以一种简洁而不失严谨性的思路，配合关键步骤的示意图，带领你熟悉红黑树的各种操作流程，同时证明它的正确性。
由于红黑树属于一种二叉搜索树，在阅读本文前，需要首先对普通二叉搜索树的原理和各种操作有所了解。

定义

根据官方定义，红黑树是一种满足如下额外条件的二叉搜索树，其中每个节点被染上红 / 黑中的一种颜色：

1. 根节点和空节点（null 指针）是黑色。
2. 从任何一个节点出发，任意向下遍历直到空节点，可能形成的所有路径上的黑节点数量是相等的。
3. 两个红节点不能是父子关系。

在这样一棵树上，所有黑节点可以看作一颗完全平衡的二叉树，而每两个黑节点之间最多只能插一个红节点进去。因此，对于任何一个节点而言，它的左右子树高度不会相差两倍以上。虽然很难严格证明它的时间复杂度，但我们可以大致感觉到，这棵树的形状一定是比较平衡的，它的查找和更新复杂度最坏是 O(logn)。
现在，不妨定义一棵子树的“黑高”为：从树根出发，向下遍历到空节点，能够遇到的黑节点数量（包括空节点和树根自身）。在这个定义下，上述的条件 2 可以简化为：

2. 所有节点的左右子树黑高必须相等。

红黑树的查找过程和普通二叉树完全相同，下面只分析它的插入和删除操作。

插入

当插入一个节点时，首先要进行一次查找判断树中是否已经存在要插入的值，如果存在就可以直接返回了。否则，我们可以任意选择插入到它的最大前缀之后，或者最小后缀之前。无论如何，要插入的新节点一定会成为叶子节点。为了简单起见，我们不妨强制规定新插入的节点是红色的。插入完成后，由于红节点不影响黑高，条件 2 显然还是满足的。如果新节点的父节点是黑色的，那么条件 3 也满足，流程可以直接结束了。否则，由于出现了两个连续的红节点，违反了条件 3，需要对树进行一些恒等变形操作来打破这种情况。这里的恒等变形指的是操作前后节点中序遍历不变，一般通过多次旋转操作实现，但我们无需关注太多细节（例如左旋还是右旋），只需记住旋转的本质是将某个特定节点提升为父节点。由于这个操作很可能需要从新节点一直迭代到树根，我们需要维护一个指针 cur 表示本次迭代正在处理的节点，初始指向新节点。这个迭代的循环不变式为：

cur 指向的节点是红色的。
cur 是根节点，或者 cur 的父节点是红色的。
cur 指向的子树满足条件 23。
cur 指向的子树黑高和插入操作前一致。

初始状态下不变式显然满足，接下来看看如何维护它。为了表述清晰，我们不妨给节点排个辈分，定义一个节点的“祖父节点”为它父节点的父节点，“叔节点”为它父节点的兄弟节点。如果 cur 不是根节点，由于它的父节点是红节点，根据条件 1，父节点也不可能是根节点，因此这样的叔节点必然存在（注意叔节点有可能是空节点）。同理，根据条件 3，祖父节点必然是黑色的，否则红色的父节点和祖父节点就连起来了。
下面，我们进行分情况讨论：

cur 就是根节点

这种情况下，为了满足条件 1，直接将 cur 的颜色变为黑色，然后结束迭代即可。不难看出，此时树根的黑高增加了 1，其它节点黑高全部不变，条件 2 依然满足。由于红变黑不可能产生连续红节点，条件 3 也满足。

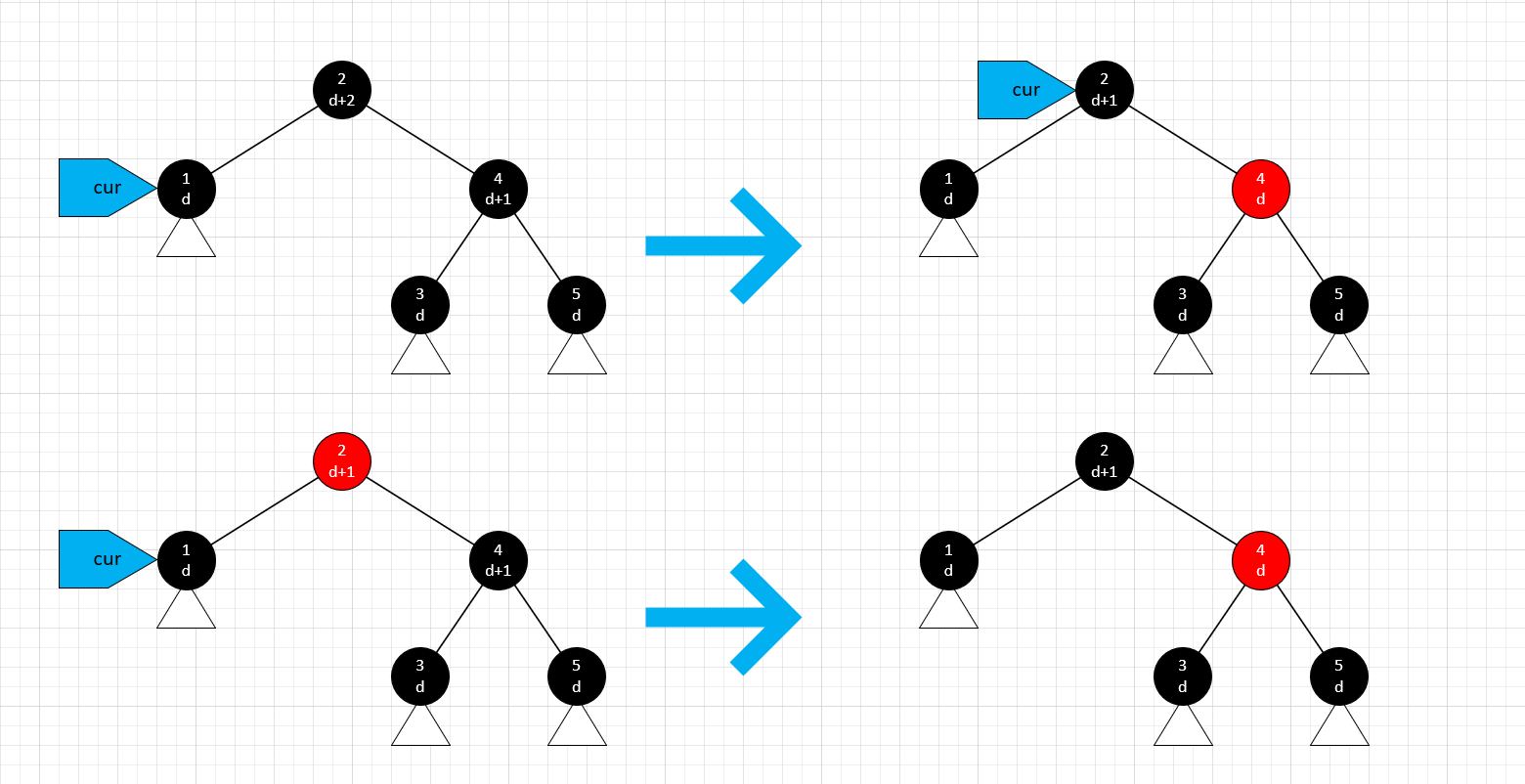
叔节点是红色

这种情况下，我们把叔节点和父节点同时变成黑色，祖父节点变成红色。如何计算操作后的黑高呢？根据定义不难看出，操作完成后，最下层带三角的 1、3、5 号节点结构不变，由于黑高是从下往上依次计算的（空节点黑高固定为 1），这些节点的黑高也不会改变，而其它节点的黑高就以它们为基准重新计算。经过计算，祖父节点本身的黑高并没有改变，两边子树黑高同时加一，不影响条件 2。看图可知，变形后的子树满足了条件 3。最后，将 cur 指向祖父节点，如果它的父节点依然是红的（或者它是根节点），就继续迭代，否则条件 3 满足，可以直接结束迭代。此时的 cur 依然满足循环不变式。

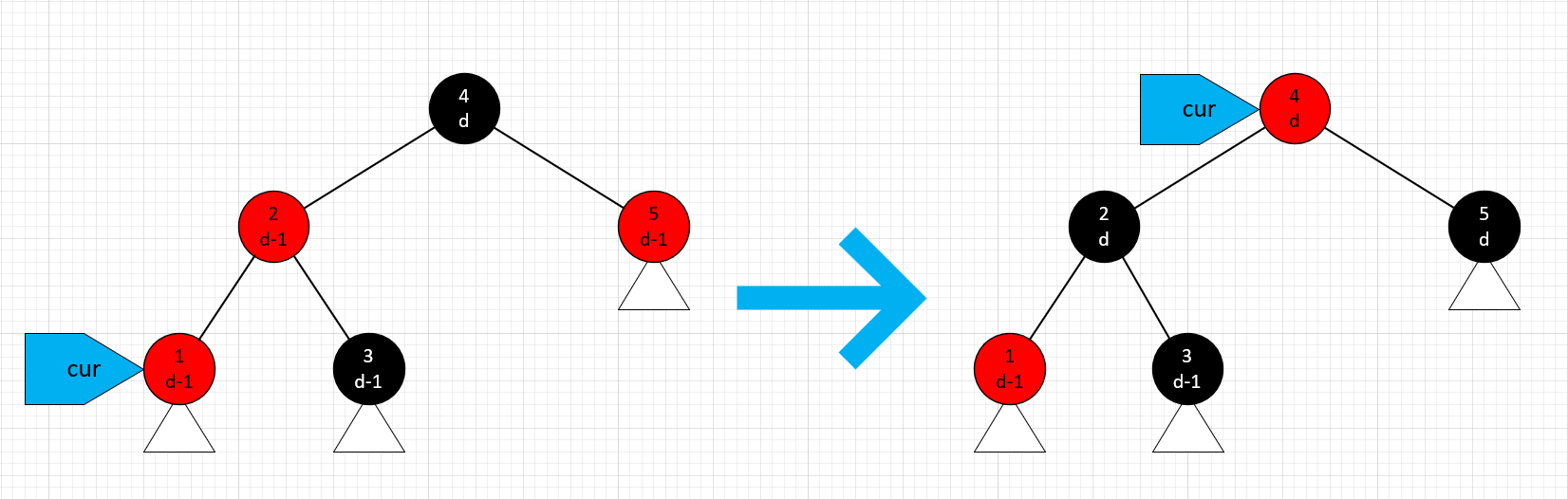
（本文的所有示意图中，节点上方的数字表示节点编号，按中序遍历顺序赋值；下方表示节点的黑高，以任意常数 d 作为基准；节点下方的三角表示任意结构的子树，在所有操作中都不会改变它的结构）

叔节点是黑色

这种情况下，我们选择 cur 和父节点中编号（注意不是位置）较靠近祖父节点的一个，将它提升到祖父位置并设为黑色，而之前的祖父节点设为红色。下图展示了 cur 分别为外侧 / 内侧儿子的两种情况，外侧儿子需要一次旋转，内侧儿子需要两次。操作完成后，树根的黑高没有改变，而其它节点的黑高也满足条件 2；由于树根为黑色，不会形成连续红节点，条件 3 也满足，迭代直接结束。

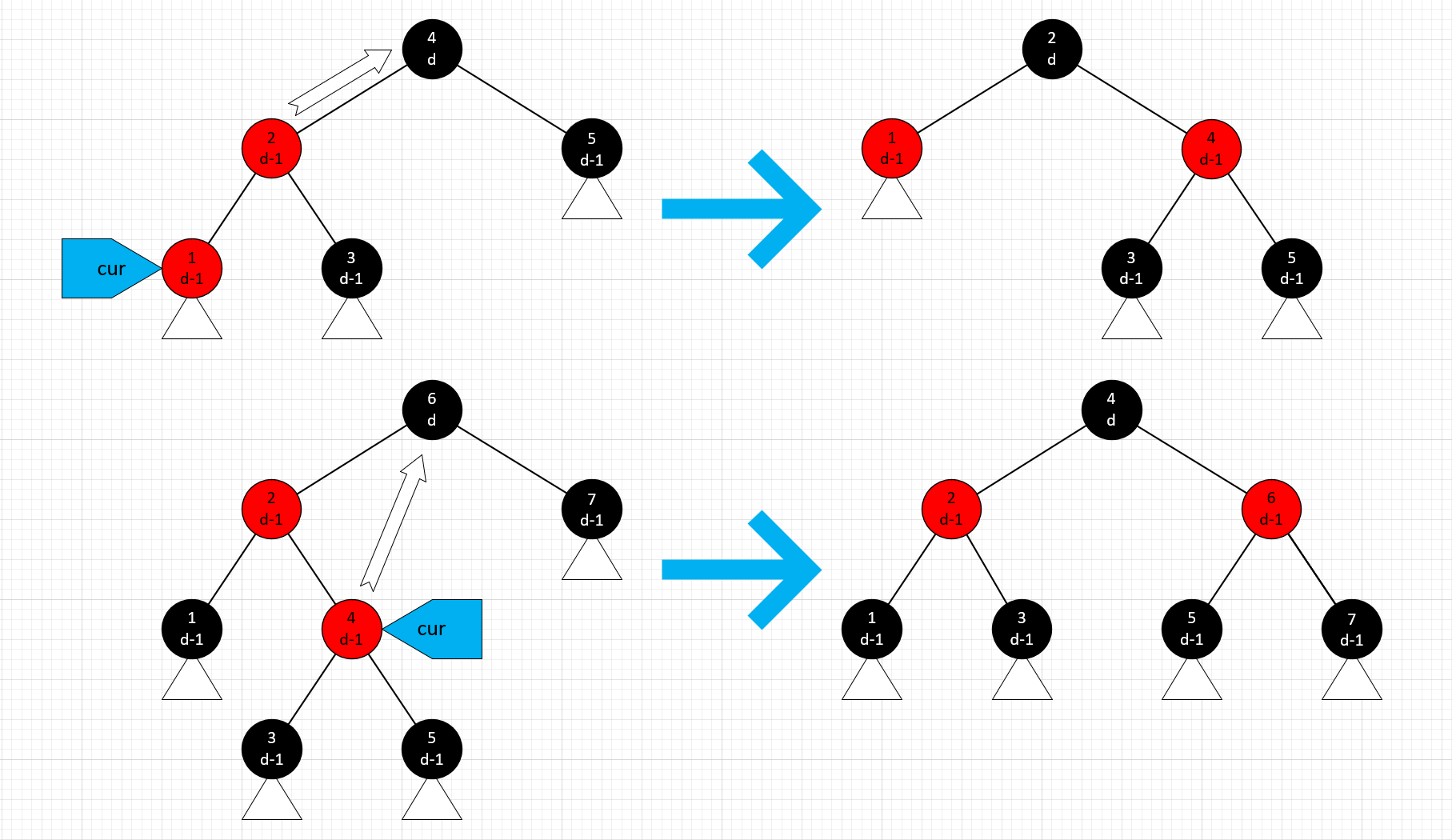
删除

当删除一个节点时，还是要执行一次查找操作判断树中有没有要删除的值，如果没有就可以直接返回了。为了简单起见，如果要删除的节点有两棵子树，我们可以在执行删除操作前，对要删除的节点和它的最大前缀或者最小后缀节点进行“值交换”，也就是只交换两个节点中的值，保持节点颜色和树结构不变。这样的操作相当于交换了有序数组中相邻的两个元素，只要随后删掉其中一个，整个数组还是有序的。同理，在执行完删除后，二叉树的有序性也不会受到影响。如此操作完后，要实际删除的节点（以下称为目标节点）就最多只有一棵子树了。我们称这棵子树为“唯一子树”，如果目标节点没有子树，那么空节点是唯一子树。
接下来，我们来考察目标节点的颜色：

如果它是红色，那么它的父节点和子节点必然是黑的。此时只需要用唯一子树替换掉目标节点。由于红节点不影响黑高，黑色的父子节点连在一起也不会产生连续红节点，条件 23 同时满足，流程直接结束。
如果它是黑色，并且子节点是红色，那么只需要用唯一子树替换掉目标节点，再将子节点设为黑色。操作后黑节点的数量不变，等价于删掉一个红节点，不影响黑高，红变黑也不会产生连续红节点，条件 23 同时满足，流程直接结束。

如果目标节点和子节点都是黑色，情况就比较麻烦了。此时还是先用唯一子树替换掉目标节点，随后还需要对整棵树进行迭代恒等变形操作。我们同样维护一个指针 cur 表示本次迭代正在处理的节点，初始指向替换后的节点。这个迭代的循环不变式为：

cur 指向的节点是黑色的。
cur 指向的子树满足条件 23。
cur 指向的子树黑高比删除操作之前少了 1。

需要注意的是，初始状态下 cur 有可能指向一个空节点，实现时需要将空节点也当作正常的黑节点来处理。遵照之前定义的辈分，我们定义一个节点的“侄节点”为它兄弟节点的子节点。首先，由于 cur 指向一个黑节点，并且它所在的子树刚才删除了一个黑节点，因此它原先的黑高至少为 2。根据条件 2，它的兄弟节点黑高也至少为 2，所以 cur 必定存在一个非空的兄弟节点。下面，我们进行分情况讨论：

兄弟节点是红色

这种情况下，根据条件 3，兄弟节点的父节点和子节点一定是黑的。我们需要将兄弟节点提升到父节点的位置，并设为黑色，而原先的父节点设为红色。此时，原先兄弟节点的外侧子节点成为了新的兄弟节点，正如之前所述，它一定是黑色的。如此一来，这种情况就被转化为了兄弟节点是黑色的情况。接下来我们不会移动 cur，而是交给后续的条件分支进一步处理。

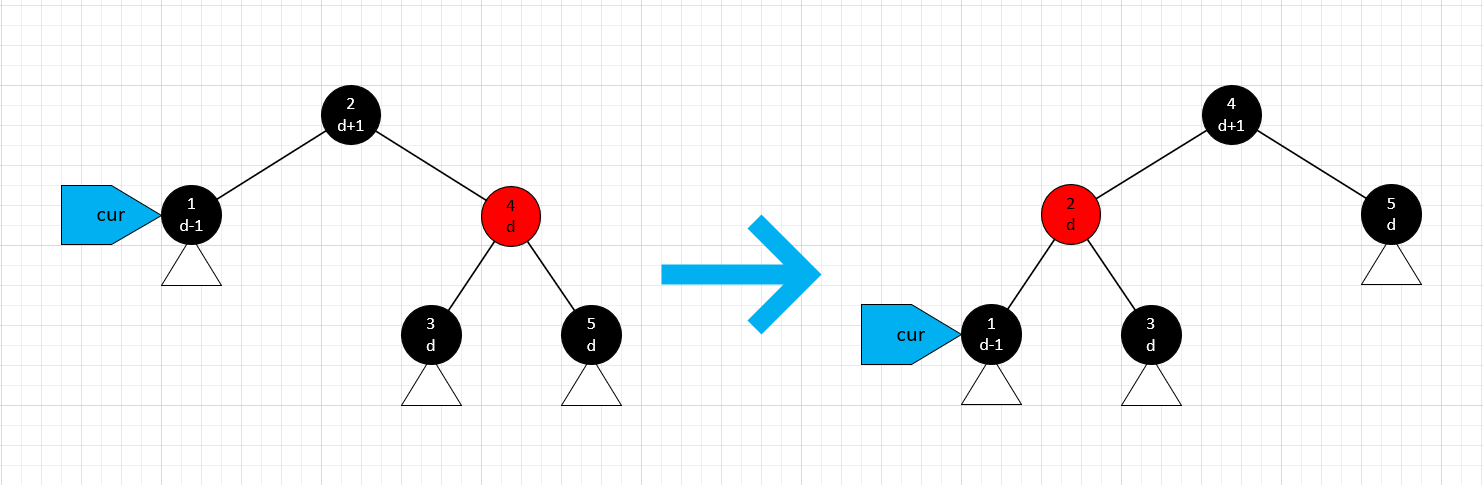
兄弟节点是黑色，侄节点至少一个是红色

这种情况有些复杂，需要分两种子情况来讨论：

外侧侄节点是红色，内侧侄节点颜色任意。此时需要将兄弟节点设为父节点的颜色，并将父节点设为黑色，随后将兄弟节点提升到父节点的位置，内侧侄节点则成为新的兄弟节点。需要一次旋转操作实现。注意虽然 5 号节点结构不变，但颜色由红变黑，自身黑高增加了 1。
内侧侄节点是红色，外侧侄节点是黑色。此时需要将内侧侄节点设为父节点的颜色，并将父节点设为黑色，随后将内侧侄节点提升到父节点的位置，它的内侧子节点则成为新的兄弟节点。需要两次旋转操作实现。
无论如何，必定能够从兄弟节点的子树中抽出一个黑高和 cur 相同的节点来作为 cur 的兄弟节点，补足它缺失的另一半。这样一来，我们就可以在它的上方引入新的黑色父节点来增加整体黑高，抵消 cur 黑高降低带来的影响，这个增加的黑高最终是由红色的侄节点变成黑色贡献的。操作完成后，条件 23 全部满足，迭代可以直接中止。

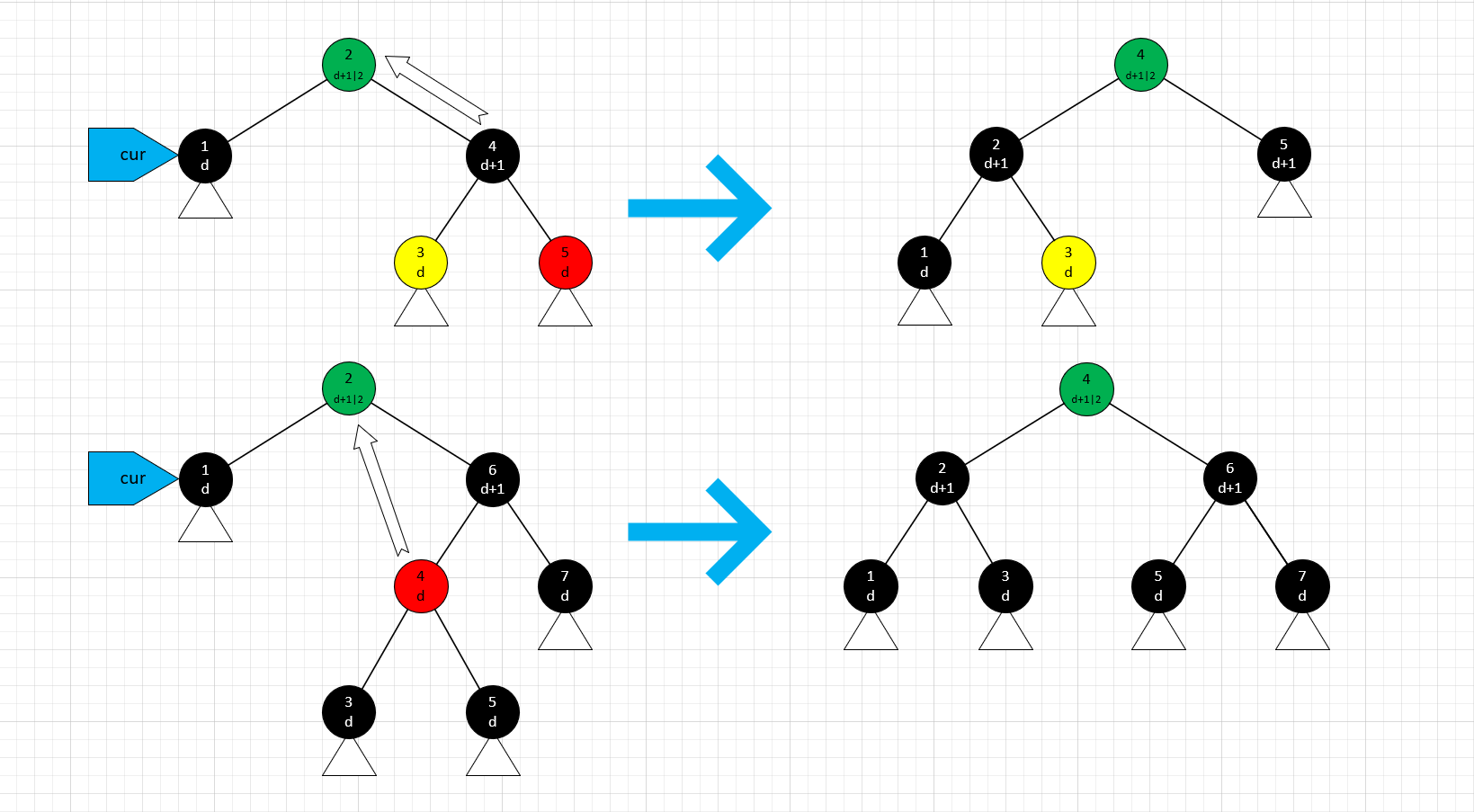
（绿色和黄色节点为颜色任意的节点，但操作前后对应颜色保持不变）

兄弟节点和侄节点都是黑色

这种情况下，需要将兄弟节点染红，然后考察父节点的颜色：

如果父节点是黑色，意味着父节点的黑高受到兄弟节点染红的影响，也减了 1。此时需要将 cur 指向父节点，继续迭代。由图可知，cur 依旧满足循环不变式。
如果父节点是红色，只需将父节点设为黑色，即可抵消黑高减 1 的影响。此时父节点黑高不变，条件 2 完全满足，而红变黑不会产生连续红节点，条件 3 满足，迭代直接结束。

总结

以上就是红黑树中全部值得一提的工作流程了。看到这里，可能不免有人产生疑惑，如此复杂而精妙的数据结构到底是怎样被发明出来的？事实上，红黑树并非完全是某位天才的灵感产物，它的前身是一种特殊的 B 树——“2-3-4 树”，这种树同样拥有自平衡性质，它的节点上可以存放 1-3 个值。至于 2-3-4 树的工作原理就超出本文的范围了，但这篇文章介绍了一种简化版本的 2-3 树及其与红黑树的关系，感兴趣的读者可自行阅读以加深理解。
最后，由于本文的部分内容是笔者的个人理解，受到知识水平限制，难免出现错误或纰漏，如有发现烦请指出，笔者不胜感激。