半年前的题解整合-526互联

前言

去年 11 ~ 12 月写了一车训练小记，选了一些当时写的题解凝炼成这篇博客。转眼半年过去了，感觉自己的能力，码风乃至题解风格都变化不小啊！

P7961 [NOIP2021] 数列

显然是一个 $dp$，首先考虑状态应如何设计。

看到 $n$ 的限制，首先可以想到记一维 $i$ 表示当前已被确定的 $a$ 序列中的元素数量。

发现该题的难点在于从低位向高维的进位难以转移，因此我们可以从低位向高位考虑。

再开一维 $j$ 表示当前考虑到了 $S$ 的第 $0\dots j$ 位，一维 $p$ 表示第 $0\dots j-1$ 向第 $j$ 位的进位为 $p$。

注意 $p$ 可以大于 $1$，即第 $j$ 位的进位暂且不以二进制形式写开。

由于还有$S$ 的二进制表示中 $1$ 不多于 $K$ 的限制，所以再记一个 $k$ 表示当前 $S$ 的第 $0\dots j-1$ 位中已有 $k$ 个 $1$。

这个时候枚举一个 $t$ 表示我们添加了多少 $2^j$ 到 $S$ 中 $(i+t\leq n)$，这样一来，如果 $p+t$ 为偶数，第 $j$ 位就会在处理掉第 $j$ 位的所有进位后变成 $0$；反之则为 $1$。所以 $(p+t)\bmod 2$ 的值即为处理掉第 $j$ 位的进位后第 $j$ 位是否为 $1$。又因为每两个 $1$ 可以向下一位进一个 $1$，所以第 $j$ 位对第 $j+1$ 位会有 $\lfloor \dfrac{p+t}{2} \rfloor$ 的进位。

综上所述，我们设计状态 $dp(i,j,k,p)$ 表示 $a$ 序列中已确定了 $i$ 个元素，当前考虑到了 $S$ 的第 $0\dots j$ 位，当前 $S$ 的第 $0\dots j-1$ 位中有 $k$ 个 $1$，第 $0\dots j-1$ 向第 $j$ 位的进位为 $p$。则 $dp(i,j,k,p)$ 会向 $dp(i+t,j+1,k+(p+t)\bmod 2,\lfloor \frac{p+t}{2} \rfloor) $ 转移（枚举 $t\in [0,n-i]$）。

由于答案满足分配律，不难想到 $dp(i,j,k,p)$ 对新状态的贡献为

\[dp(i,j,k,p) \times {i+t\choose t}\times v_j^t \]

预处理一下组合数和 $v_j$ 的幂次，即可做到 $\mathcal{O}(n^4m)$ 转移。

~~转移的时候先枚举 $j$ 再枚举 $i$ 好像合理一些，但是先 $i$ 后 $j$ 也过了QwQ~~

那么如何统计答案呢？由转移的过程不难想到统计答案时需要枚举 $dp(n,m+1,?,?)$，枚举 $k,p$ 即可。

当 $k+\mathrm{popcnt}(p)\leq K$ 时答案是合法的，因为第 $m+1$ 位的进位还会让 $S$ 中新增 $\mathrm{popcnt}(p)$ 个 $1$。

// 代码中交换了 i 与 j 的定义
for(int i=0;i<=m;++i){
  for(int j=0;j<=n;++j){
    for(int k=0;k<=K;++k){
      for(int p=0;p<=n;++p){
        for(int t=0;t<=n-j;++t)
          dp[i+1][j+t][k+(t+p&1)][t+p>>1]+=
          dp[i][j][k][p]*C[j+t][t]%mod*pv[i][t]%mod;
      }
    }
  }
}
i64 ans=0;
for(int k=0;k<=K;++k){
  for(int p=0;p<=n;++p){
    if(k+popcount(p)<=K) (ans+=dp[m+1][n][k][p])%=mod;
  }
}

P7140 [THUPC2021 初赛] 区间矩阵乘法

不难发现 $d$ 的值域是根号级别的。猜想正解是一种 $\mathcal{O}(n\sqrt n)$ 的做法。

先来化简一下要求的式子

\[\begin{align} \sum_{i=0}^{d-1} \sum_{j=0}^{d-1} \sum_{k=0}^{d-1} a_{p_1+d\cdot i+j} a_{p_2 + d\cdot j + k} &=\sum_{i=0}^{d-1}\sum_{j=0}^{d-1}a_{p_1+j+d\cdot i}\sum_{k=0}^{d-1}{a_{p_2+d\cdot j+k}}\\ &=\sum_{j=0}^{d-1}(sum_{p_2+d \cdot (j+1)-1}-sum_{p_2+d \cdot j-1})\sum_{i=0}^{d-1}{a_{p_1+j+d \cdot i}} \end{align} \]

如果使用同余前缀和（记 $s_{i,j}$ 表示 $\sum_{i=0}^{\lfloor \frac{j}{i} \rfloor}{a_{j-d \cdot i}}$ ），后面那个 $\sum$ 可以用同余前缀和 $\mathcal{O}(1)$ 求出。

暴力遍历 $j \gets [0,d-1]$ 的复杂度是 $\mathcal{O}(\sqrt n)$ 的，而 $s$ 可以通过递推式

\[s_{i,j}=\left\{ \begin{array}{ll} a_j,j\leq i\\ s_{i,j-i}+a_j,j>i \end{array} \right. \]

$\mathcal{O}(n\sqrt n)$ 预处理出。所以总时间复杂度 $\mathcal{O}((n+m)\sqrt n)$；空间复杂度 $\mathcal{O}(n\sqrt n)$，如果动态处理前缀和可以做到 $\mathcal{O}(n)。$

（最终的式子：$\sum_{j=0}^{d-1}(sum_{p_2+d \cdot (j+1)-1}-sum_{p_2+d \cdot j-1})(s_{p_1+j+d(d-1)}-s_{p_1+j}+a_{p_1+j})$，这里的 $sum_j$ 亦可写作 $s_{1,j}$）

void build(int n){
	int block=sqrt(n)+1;
	for(int i=1;i<=block;++i){
		for(int j=1;j<=n;++j){
			if(j<=i) s[i][j]=a[j];
			else s[i][j]=s[i][j-i]+a[j];
		}
	}
}
inline i32 query(int d,int p1,int p2){
	ans=0;
	for(int j=0;j<=d-1;++j) 
		ans+=(s[1][p2+d*(j+1)-1]-s[1][p2+d*j-1])*(s[d][p1+j+d*(d-1)]-s[d][p1+j]+a[p1+j]);
	return ans;
}

P7145 [THUPC2021 初赛] 合法序列

看到 $k\leq 4$ 和二进制，不难想到是一个状压 $dp$。

由于 $2^k \leq 16$，所以可以先枚举第 $0\dots2^k-1$ 位的数，对于其中合法的情况，记 $dp(i,s)$ 表示当前考虑到第 $i$ 位，以第 $i$ 位为末尾的末 $k$ 位为 $s$ 的方案数。时间复杂度 $\mathcal{O}(2^{2^k} \times 2^k \times n)$。

$dp(i,s)=dp(i-1,s>>1)[a_{s>>1}=1]+dp(i-1,(s>>1)|(1<<(k-1)))[a_{(s>>1)|(1<<(k-1))}=1]$

inline int calc(int x){
	int ret=0;
	for(int i=x;i<x+k;++i){
		ret<<=1;
		ret|=a[i];
	}
	return ret;
}
void solve(int x){
	for(int i=(1<<k)-1;i>=0;--i,x>>=1) a[i]=(x&1);
	for(int i=0;i<=(1<<k)-k;++i){
		int val=calc(i);
		if(a[val]==0) return;
	}
	memset(dp,0,sizeof(dp));
	dp[calc((1<<k)-k)][(1<<k)-1]=1;
	for(int i=(1<<k);i<n;++i){
		for(int s=0;s<(1<<k);++s){
			if(!a[s]) continue;
			if(a[s>>1]) dp[s][i]=dp[s>>1][i-1];
			if(a[(s>>1)|(1<<k-1)]) dp[s][i]+=dp[(s>>1)|(1<<k-1)][i-1];
			if(dp[s][i]>mod) dp[s][i]-=mod;
		}
	}
	for(int s=0;s<(1<<k);++s){
		if(!a[s]) continue;
		ans+=dp[s][n-1];
		if(ans>mod) ans-=mod;
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);cout.tie(nullptr);
	cin>>n>>k;
	for(int i=0;i<(1<<(1<<k));++i) solve(i);
	cout<<ans;
}

~~好像有大佬用AC自动机上dp，我大受震撼~~

P7137 [THUPC2021 初赛] 切切糕

考虑 $dp(i,j)$ 表示已考虑了前 $i$ 个切糕，Tinytree 使用了 $j$ 次"优先选糕权"时 Tinytree 的最大得分。

则有 $dp(i,j)=\max (dp(i-1,j)+x,dp(i-1,j-1)+a_i-x)$，其中 $x$ 由 Kiana 决定。

而对 Kiana 而言，为了最小化 Tinytree 得到的切糕总数，他可以

\[\left\{ \begin{array}{ll} 改变 a 中元素的排列顺序\\ 调整 x 的值 \end{array} \right. \]

$x=\frac{dp(i-1,j-1)-dp(i-1,j)+a_i}{2}$ 时可以使二者相等，但是仅靠这个方程解出来的 $x$ 是有可能为负数的，考虑到 $dp(i,j)$ 应不劣于 $dp(i-1,j)$，因此与 $dp(i-1,j)$ 取个 $\max$。（从实际意义上讲，如果能切出负数，那么 Tinytree 不使用优先权所能得到的切糕为 $0$，因此可以直接由 $dp(i-1,j)$ 转移）

$a$ 序列的排列顺序为从大到小排列时答案是最优的，这一点可以用微扰法来证明。（感性理解一下，当 $a$ 呈递减排列时转移过程中的 $x$ 的值是更小甚至为负的，这样一来转移过程中产生的增量就小了，自然 $dp(n,m)$ 也会变小）

#include <bits/stdc++.h>
using namespace std;
using f128 = long double;
const int N = 2500 + 5;
f128 dp[N][N];
int a[N], n, m;
bool cmp(int x, int y){return x > y;}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> m;
	for(int i = 1; i <= n; ++i) cin >> a[i];
	sort(a + 1, a + n + 1, cmp);
	int sum = 0;
	for(int i = 1; i <= n; ++i){
		sum += a[i];
		dp[i][i] = sum/2.0;
		for(int j = min(i - 1, m); j >= 1; --j){
			f128 x = (dp[i - 1][j - 1] - dp[i - 1][j] + a[i]) / 2;
			dp[i][j] = max(dp[i - 1][j], dp[i - 1][j] + x);
		}
	}
	cout << setprecision(10) << fixed << sum - dp[n][m];
}

P8850 [JRKSJ R5] Jalapeno and Garlic

大佬：常系数线性递推
~~我： Mathematica~~

记 $f_i$ 表示沿顺时针方向距目标 $i$ 格时从该点到目标的期望步数。

则 $f_i=1+\frac{1}{2}(f_{i-1}+f_{i+1})$ 。

然后~~默默打开MMA~~可以使用常系数线性递推的方法（转载）

$F(x)=2xF(x)-x^2F(x)-\dfrac{2x}{1-x}+(f_1+2)x,f_i=i(f_1-i+1)$，进而由 $f_0=0$ 得解。

总之最终得到了 $f_i=i(n-i)$。

记 $v_d$ 表示以点 $d$ 为目标时的答案。则有

\[\begin{align} v_d&=\sum_{i=1}^{n}{a_i \cdot f(|d-i|)}\\ &=\sum_{i=1}^{d-1}{a_i \cdot f(d-i)} + \sum_{i=d+1}^{n}{a_i \cdot f(i-d)} \end{align} \]

记 $A=\sum_{i=1}^{d-1}{a_i(d-i)(n-d+i)},B=\sum_{i=d+1}^{n}{a_i(i-d)(n+d-i)}$

乘积展开并按 $\sum$ 分类，得到

\[A=d(n-d)\sum_{i=1}^{d-1}{a_i} + (2d-n)\sum_{i=1}^{d-1}{ia_i} - \sum_{i=1}^{d-1}{i^2a_i} \]

\[B=-d(n+d)\sum_{i=d+1}^{n}{a_i} + (2d+n)\sum_{i=d+1}^{n}{ia_i} - \sum_{i=d+1}^{n}{i^2a_i} \]

$\mathcal{O}(n)$ 预处理前缀和，后缀和就做完了，$v_d=A+B$，注意要 int128。

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using i128 = __int128;

const int N = 1e6 + 5, mod = 1004535809;

int a[N];
i128 pre[3][N], suf[3][N];

int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int n; cin >> n;
	for(int i = 1; i <= n; i++)
        cin >> a[i];
	for(i128 i = 1; i <= n; i++){
		pre[0][i] = pre[0][i - 1] + a[i];
		pre[1][i] = pre[1][i - 1] + i * a[i];
		pre[2][i] = pre[2][i - 1] + i * i * a[i];
	}
	for(i128 i = n; i >= 1; i--){
		suf[0][i] = suf[0][i + 1] + a[i];
		suf[1][i] = suf[1][i + 1] + i * a[i];
		suf[2][i] = suf[2][i + 1] + i * i * a[i];
	}
	i128 A, B, res, ans;
	for(i128 d = 1; d <= n; d++){
		A = d * (n - d) * pre[0][d - 1] + (2 * d - n) * pre[1][d - 1] - pre[2][d - 1];
		B = -d * (n + d) * suf[0][d + 1] + (2 * d + n) * suf[1][d + 1] - suf[2][d + 1];
		if(d == 1) ans = A + B;
		else ans = min(ans, A + B);
	}
	i64 x = ans % mod;
	cout << x;
}

P8849 『JROI-7』hibernal

二进制分组的思想，唯一确定最终结果。

CF1748 D. ConstructOR

发现 $a,b,d < 2^{30}$ 而 $x < 2^{60}$，考虑构造一个 $x$ 使得 $x$ 的 $[\mathrm{lowbit}(d),30)$ 位均为 $1$ 且 $x$ 是 $d$ 的倍数，这样一来同时保证了 $a|x = b|x = x$。对 $[\mathrm{lowbit}(d),30)$ 位扫一遍即可。

void solve(){
	i64 a, b, d;
	cin >> a >> b >> d;
	if(min(__builtin_ffs(a), __builtin_ffs(b)) < __builtin_ffs(d)){
		cout << "-1\n";
		return;
	}
	int c = __builtin_ctz(d);
	i64 res = 0;
	for(int i = c; i < 30; ++i){
		if((res >> i) & 1) continue;
		res += (d << (i - c));
	}
	cout << res << '\n';
}

CF1748 F. Circular Xor Reversal

首先只考虑两个数 $a_i,a_j$，可以通过以下的异或操作实现交换操作：

\[\begin{align} a_i \gets a_i \oplus a_j \\ a_j \gets a_i \oplus a_j \\ a_i \gets a_i \oplus a_j \end{align} \]

那么，如何类比到这道题呢？我们一步一步考虑。

算法 1

一种比较容易的思路是考虑如何使 $a_i \gets a_i \oplus a_j$。下文为简化叙述，记一个长为 $m$ 的数组 $b$，并记 $(l \dots r)$ 表示 $\oplus_{i=l}^{r}{b_i}$，$(l,r)$ 表示 $b_l \oplus b_r$。

考虑如何使 $b_0 \gets b_0 \oplus b_m$。首先从 $m-1$ 向 $0$ 扫一遍，此时的序列状态为：

\[b=[(0 \dots m),(1 \dots m),\dots,(m-1 \dots m),m] \]

因为要让 $b_0 \gets (0,m)$，所以递推地考虑能不能让 $b_1 \gets (1 \dots m-1)$。所以接下来可以从 $1$ 向 $m-1$ 扫一遍，再从 $m-2$ 向 $1$ 扫一遍：

\[b=[(0 \dots m),1,2,\dots,m-1,m] \]

\[b=[(0 \dots m),(1 \dots m-1),(2 \dots m-1),\dots,(m-2 \dots m-1),m-1,m] \]

这样一来再从 $0$ 向 $m-2$ 扫一遍，最终得到了：

\[b=[(0,m),1,2,\dots,m-1,m] \]

简单的分析一下，容易发现完成一次异或操作的复杂度达到了 $4m$ 的量级，完成一次交换操作就大概需要 $4n+4m$ 的操作量了，原序列需要 $\mathrm{swap}$ $\frac{n}{2}$ 次，因此我们大概需要 $2n^2+2nm$ 的操作量。然而这个题~~很毒瘤~~只留了 $250000$ 次操作机会，而 $2n^2$ 就已经达到 $320000$ 了。

算法 2

分析一下构造数组 $b$ 的过程，不难发现在我们枚举 $\mathrm{swap}$ 的时候是存在很多重复步骤的！因此想到如何尽量避免重复步骤。单次 $\mathrm{swap}$ 的过程显然没什么可优化的，所以考虑是否能减少 $\mathrm{swap}$ 的次数，是否能整体考虑等。

事实上是可以整体考虑的。观察算法 1 中构造 $b$ 数组的过程，容易发现得到 $b=[(0 \dots m),1,2,\dots,m-1,m]$ 是只需要 $2m$ 的操作数的。继续归纳的话，我们不难构造出如下的数组 $b$：

\[b=\left\{ \begin{array}{ll} [(0 \dots m),(1 \dots m-1),(2 \dots m-2),\dots,(\frac{m}{2}-1 \dots \frac{m}{2}+1),\frac{m}{2},\dots,m-1,m],m为偶数\\ [(0 \dots m),(1 \dots m-1),(2 \dots m-2),\dots,(\frac{m-1}{2} \dots \frac{m+1}{2}),\frac{m+1}{2},\dots,m-1,m],m为奇数 \end{array} \right. \]

最后从 $0$ 向 $\lfloor \frac{m}{2} \rfloor - 1$ 扫一遍即可得到：

\[b=\left\{ \begin{array}{ll} [(0,m),(1,m-1),(2,m-2),\dots,(\frac{m}{2}-1,\frac{m}{2}+1),\frac{m}{2},\dots,m-1,m],m为偶数\\ [(0,m),(1,m-1),(2,m-2),\dots,(\frac{m-1}{2},\frac{m+1}{2}),\frac{m+1}{2},\dots,m-1,m],m为奇数 \end{array} \right. \]

记将 $a$ 数组中的一段 $[l,r]$ 变为如上形式的过程为 $f(l,r)$。（即取出 $a$ 数组中的 $[l,r]$ 段作为 $b$ 数组时的操作过程）

（注意原题意中 $a$ 数组可以视作一个环，所以 $l>r$ 时意为 $[l,n-1] \cup [0,r]$）

（以下叙述默认 $n$ 为偶数）我们先试着执行一次 $f(0,n-1)$，发生改变的部分对应着上图中的 $A$ 部分。这和开篇提到的交换有异曲同工之妙，如果我们接着执行 $f(\frac{n}{2},\frac{n}{2}-1)$，发生改变的部分对应上图 $B$ 部分。所以我们把 $A,B$ 部分视为整体，可以得到一个大概的思路：依次进行 $f(0,n-1),f(\frac{n}{2},\frac{n}{2}-1),f(0,n-1)$，改变 $A,B,A$。注意 $A,B$ 两部分中编号相同的位置，拿 $1$ 举例：

当我们通过操作 $f(0,n-1)$ 改变了 $A$ 部分时，$A_1 \gets A_1 \oplus B_1$，即 $a_0 \gets a_0 \oplus a_{n-1}$
当我们通过操作 $f(\frac{n}{2},\frac{n}{2}-1)$ 改变了 $B$ 部分时，$B_1 \gets A_1 \oplus B_1$，即 $a_{n-1} \gets a_0 \oplus a_{n-1}$
最后一步通过操作 $f(0,n-1)$ 改变了 $A$ 部分时，$A_1 \gets A_1 \oplus B_1$，即 $a_0 \gets a_0 \oplus a_{n-1}$

上述操作过程对于其它编号同理。最终我们便成功反转了 $a$ 序列。

不妨分析一下复杂度，每次执行 $f$ 时操作次数为 $m+(m-1)+\dots+1+\frac{m}{2}=\frac{m^2+2m}{2}$。因此解决该题共需 $\frac{3}{2} (m^2+2m)$ 次操作。显然有 $m\leq n\leq 400$，故 $\frac{3}{2} (m^2+2m)\leq 241200$，可以通过。

摆一下结论：

若 $n$ 为偶数，依次执行 $f(0,n-1),f(\frac{n}{2},\frac{n}{2}-1),f(0,n-1)$ 即可反转序列。
若 $n$ 为奇数，依次执行 $f(0,n-1),f(\frac{n+1}{2},\frac{n-1}{2}-1),f(0,n-1)$ 即可反转序列。

vector<int> ans;
int n;
inline void work(int l, int r){
	if(l > r) r += n;
	int opl = l, m = r - l;
	for(int i = 1; l <= r; i ^= 1){
		if(i){
			r--;
			for(int j = r; j >= l; --j)
				ans.push_back(j);
		}else{
			l++;
			for(int j = l; j <= r; ++j)
				ans.push_back(j);
		}
	}
	for(int i = opl; i < opl + m / 2; ++i) ans.push_back(i);
}
void solve(){
	cin >> n;
	if(n & 1){
		work(0, n - 1);
		work((n + 1) / 2, (n - 1) / 2 - 1);
		work(0, n - 1);
	}else{
		work(0, n - 1);
		work(n / 2, n / 2 - 1);
		work(0, n - 1);
	}
	cout << ans.size() << '\n';
	for(auto &x : ans) cout << x % n << ' ';
}

后记：这是本人第一次尝试 *3000 的题目，也是本人第一次 AC 了洛谷上的一道黑题。很感动。

CF1420 D. Rescue Nibel!

经典的区间覆盖问题。

两个区间有交集当且仅当 $\max(l_1,l_2) \leq \min(r_1,r_2)$，因此这个问题可以转化为二维偏序问题。考虑定一动一，按左端点升序排序。只需计算前 $i-1$ 个区间有多少个 $r \geq l_i$。记这个值为 $cnt_{i-1}$，那么第 $i$ 个区间对答案的贡献为 $\binom{cnt_{i-1}}{k-1}$。

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 mod = 998244353, N = 3e5 + 5, M = N << 1;
struct segment{
	int l, r;
	bool operator < (const segment &x) const {return l < x.l;}
}seg[N];
int t[M], dsu[M], cnt[N];
inline void add(int x){for(; x < M; x += x & (-x)) t[x]++;}
inline int query_s(int x){int res = 0; for(; x; x -= x & (-x)) res += t[x]; return res;}
inline int query(int x, int y){return query_s(y) - query_s(x - 1);}
i64 fac[N];
inline i64 ksm(i64 a, i64 b, i64 p){
	i64 res = 1;
	while(b){
		if(b & 1) res = res * a % p;
		a = a * a % p; b >>= 1;
	}
	return res;
}
inline i64 inv(i64 x){return ksm(x, mod - 2, mod);}
inline i64 binom(i64 n, i64 m){
	if(m > n) return 0;
	return fac[n] * inv(fac[m]) % mod * inv(fac[n - m]) % mod;
}
void solve(){
	int n, k, m = 0;
	cin >> n >> k;
	for(int i = 1; i <= n; ++i){
		cin >> seg[i].l >> seg[i].r;
		dsu[++m] = seg[i].l, dsu[++m] = seg[i].r;
	}
	sort(dsu + 1, dsu + m + 1);
	m = unique(dsu + 1, dsu + m + 1) - dsu - 1;
	for(int i = 1; i <= n; ++i){
		seg[i].l = lower_bound(dsu + 1, dsu + m + 1, seg[i].l) - dsu;
		seg[i].r = lower_bound(dsu + 1, dsu + m + 1, seg[i].r) - dsu;
	}
	sort(seg + 1, seg + n + 1);
	i64 ans = 0;
	for(int i = 1; i <= n; ++i){
		cnt[i - 1] = query(seg[i].l, m);
		add(seg[i].r);
		ans = (ans + binom(cnt[i - 1], k - 1)) % mod;
	}
	cout << ans;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	fac[0] = 1;
	for(int i = 1; i < N; ++i) fac[i] = fac[i-1] * i % mod;
	solve();
}

CF1747 E. List Generation

期中考试数学的时候做出来的qwq

首先可以将问题转化为：给定一张 $(n+1)\times(m+1)$（纵坐标范围 $[0,n]$，横坐标范围 $[0,m]$）的网格图，求满足至少有一条只向下或向右的从 $(0,0)$ 到 $(n,m)$ 的路径经过点集内所有点的本质不同点集大小和。

显然一个点集可以归属于不同的路径，因此本题难点在于如何不重不漏地统计答案。下文给出一种不需要容斥的做法。

我们考虑找到一种分类方式使得每个点集仅被归属于一条路径。发现一条路径上一定存在一些拐点，也是这些拐点唯一确定了这一条路径。如下图红色网格即各个拐点。

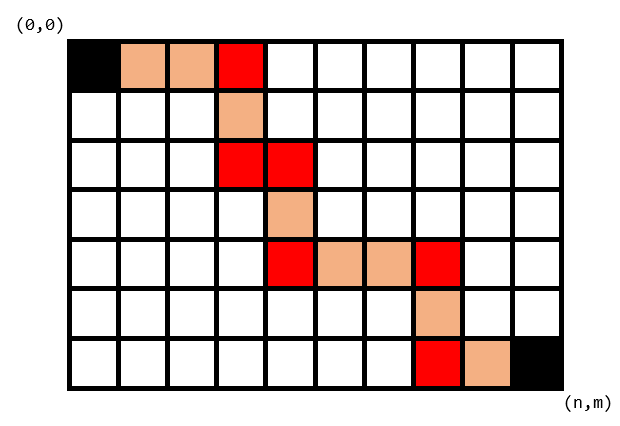
这启示我们可以进一步将这个路径划分成若干个先向右再向下的结构（向右与向下至少 $1$ 格），并将结构的终点称作结点，如下图红色部分就是该路径的结点。特别地，我们记纵坐标为 $n$ 或横坐标为 $0$ 的结点被 $(0,0)$ 或 $(n,m)$ 直接连接，如最下面那个结点。容易发现不同的结点点集对应的路径一定不同。

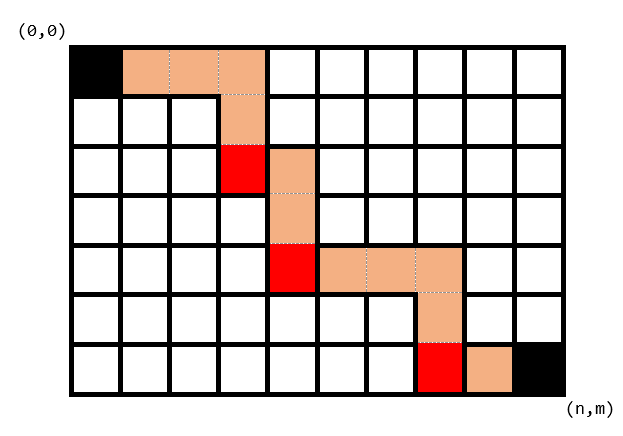
枚举结点是容易的，对于我们当前枚举到的结点点集，钦定我们一定会选择其中所有的结点，及 $(0,0),(n,m)$ 两点，路径上的剩余部分则可以任选，这样一来，我们得到的总点集归属且仅归属于一个结点点集，成功做到了不重不漏。

思路清楚后，公式推导就简单了。记输出答案为 $Ans(n,m)$，并记 $n \leq m$，则

\[Ans(n,m) = \sum_{k=0} ^ {n} \binom{n}{k} \binom{m}{k} \sum_{i=0} ^ {n + m - 1 - k} \binom{n + m - 1 - k}{i} (k+2+i) \]

解释一下这个公式，最外层的 $\sum_{k=0} ^ {n} \binom{n}{k} \binom{m}{k}$ 是在枚举结点集，其中 $k$ 指结点集的大小，每个结点的纵坐标范围在 $[1,n]$，横坐标范围在 $[0,m-1]$。记 $s=n+m-1-k$ 代表除去结点点集和 $(0,0),(n,m)$ 后路径上剩余的点的数量，则

\[\sum_{i=0} ^{s} {\binom{s}{i}(k+2+i)} \]

计算的是在剩余点中进行选择后对 $Ans(n,m)$ 的贡献，其中 $i$ 枚举的是选择了 $i$ 个点， $(k+2+i)$ 指当前的总点集大小。

直接计算的话是 $\mathcal{O}(n(n+m))$ 的，重新考虑一下 $\sum_{i=0} ^{s} {\binom{s}{i}(k+2+i)}$ 这个式子，可以将它拆成 $(k+2) 2^s + \sum_{i=0} ^ {s} {\binom{s}{i}i}$。考虑到组合数具有对称性，有 $\sum_{i=0} ^ {s} {\binom{s}{i}i} = \sum_{i=0} ^ {s} {\binom{s}{i}(s-i)}$，我们把两者加起来除以 $2$ 就可以得到 $\sum_{i=0} ^ {s} {\binom{s}{i}i} = s2^{s-1}$ 了。时间复杂度 $\mathcal{O}(n)$。

void solve(){
	int n, m;
	cin >> n >> m;
	if(n > m) swap(n, m);
	i64 ans = 0, tmp = 0, s;
	for(int k = 0; k <= n; ++k){
		s = n + m - 1 - k;
		tmp = s * pw2[s - 1] + 1LL * (k + 2) * pw2[s];
		tmp %= mod;
		ans += binom(n, k) * binom(m, k) % mod * tmp % mod;
		ans %= mod;
	}
	cout << ans << '\n';
}

CF1175 F. The Number of Subpermutations

CF1746 F. Kazaee

P3792 由乃与大母神原型和偶像崇拜

CF869 E. The Untended Antiquity

CF1418 G. Three Occurrences

见哈希算法学习笔记 I：XOR hashing

P8858 折线

观察样例就会发现答案只可能在 $[2,4]$。感性理解一下，一条起止任意且拥有两个折点的折线可以将平面任意划分，为了将起止与 $(0,0),(10^{100},10^{100})$ 连接还需两个折点，因此答案的上界为 $4$。

当答案为 $2$ 时，一定存在一条直线 $x=a$ 或 $y=a$ 使得平面被划分成的两部分点数相等。动态维护其中一部分有多少个点即可。

当答案为 $3$ 时，一定存在一个位于右下方/左上方的矩形使得矩形内的点数与另一部分相等。考虑位于右下方的情况，则问题可以抽象成：判断是否存在一点 $(x_0,y_0)$，使得满足 $x_i \geq x_0,y_i \leq y_0$ 的点数为 $\frac{n}{2}$。类似于一个二维偏序问题，我们考虑先按 $x$ 从大到小，$y$ 从小到大对所有点排序，树状数组维护合法点数，同时枚举 $x_0 \in \{x_i\}$。由于随着 $y_0$ 增大，合法的点数只增不减，利用这一单调性可以二分 $y_0$。

int t[N], n;
inline void add(int x){for(; x <= n; x += x & (-x)) t[x]++;}
inline int query(int x){int ret = 0; for(; x; x -= x & (-x)) ret += t[x]; return ret;}
struct point{
	int x, y;
}pt[N];
inline bool cmp1(point &a, point &b){return a.x < b.x;}
inline bool cmp2(point &a, point &b){return a.y < b.y;}
inline bool cmp3(point &a, point &b){if(a.x == b.x) return a.y < b.y; return a.x > b.x;}
inline bool cmp4(point &a, point &b){if(a.y == b.y) return a.x < b.x; return a.y > b.y;}
void solve(){
	cin >> n;
	for(int i = 1; i <= n; ++i) cin >> pt[i].x >> pt[i].y;
	sort(pt + 1, pt + n + 1, cmp1);
	int cnt = 0, cur = 0, last = 0;
	for(int i = 1; i <= n; ++i){
		if(pt[i].x == last) ++cur;
		else{
			cnt += cur;
			if(cnt == n / 2){
				cout << "2\n";
				return;
			}else if(cnt > n / 2) break;
			cur = 1;
			last = pt[i].x;
		}
	}
	sort(pt + 1, pt + n + 1, cmp2);
	cnt = 0, cur = 0, last = 0;
	for(int i = 1; i <= n; ++i){
		if(pt[i].y == last) ++cur;
		else{
			cnt += cur;
			if(cnt == n / 2){
				cout << "2\n";
				return;
			}else if(cnt > n / 2) break;
			cur = 1;
			last = pt[i].y;
		}
	}
	for(int i = 1; i <= n; ++i) t[i] = 0;
	sort(pt + 1, pt + n + 1, cmp3);
	for(int i = 1; i <= n; ++i){
		add(pt[i].y);
		if(pt[i].x != pt[i + 1].x){
			int l = 1, r = n, mid;
			while(l <= r){
				mid = (l + r) >> 1;
				cur = query(mid);
				if(cur == n / 2){
					cout << "3\n";
					return;
				}else if(cur > n / 2) r = mid - 1;
				else l = mid + 1;
			}
		}
	}
	for(int i = 1; i <= n; ++i) t[i] = 0;
	sort(pt + 1, pt + n + 1, cmp4);
	for(int i = 1; i <= n; ++i){
		add(pt[i].x);
		if(pt[i].y != pt[i + 1].y){
			int l = 1, r = n, mid;
			while(l <= r){
				mid = (l + r) >> 1;
				cur = query(mid);
				if(cur == n / 2){
					cout << "3\n";
					return;
				}else if(cur > n / 2) r = mid - 1;
				else l = mid + 1;
			}
		}	
	}
	cout << "4\n";
}

CF1761 D. Carry Bit

下文起用 $a_i,b_i$ 表示其二进制表示下的第 $i$ 位（1-indexed）。

人类智慧地想到记 $c_i$ 表示第 $i$ 位向第 $i + 1$ 位进位的值（1-indexed，$i \in [1,n]$），且 $c_0 = 0$。

这样一来，由 $c_i$ 其实是可以直接确定 $(a_i,b_i)$ 的。具体来讲可以分以下四类：

$c_i = 0, c_{i - 1} = 0$，则 $(a_i,b_i) = (0,0),(0,1),(1,0)$
$c_i = 0, c_{i - 1} = 1$，则 $(a_i,b_i) = (0,0)$
$c_i = 1, c_{i - 1} = 0$，则 $(a_i,b_i) = (1,1)$
$c_i = 1, c_{i - 1} = 1$，则 $(a_i,b_i) = (0,1),(1,0),(1,1)$

因此当 $c_i = c_{i - 1}$ 时，$(a_i,b_i)$ 有 $3$ 种可能；当 $c_i \neq c_{i - 1}$ 时，$(a_i,b_i)$ 只有 $1$ 种可能。

枚举一个 $q$ 表示 $c$ 中满足 $c_i \neq c_{i - 1}(i \in [1,n])$ 的 $i$ 的总数，则对于这样的 $c$，我们有 $3^{n - q}$ 种 $(a,b)$。

下面的问题是，如何计算满足 $c_i \neq c_{i - 1}$ 的总数为 $q$，且最终 $f(a,b) = k$ 的 $c$ 的方案数。

首先考虑 $q$ 的限制带来了什么。观察到 $c$ 一定是由若干个 $1$ 与若干个 $0$ 交替组成的（e.g. $c = \{0, 1, 1, 0, 1, 1, 0, 0\}$）。而每一段极长的 $0$ 与极长的 $1$ 的交汇处都会有一处 $c_i \neq c_{i - 1}$，不难得到 $c$ 中会有 $\lceil {\frac{q + 1}{2}}\rceil$ 段极长的 $0$ 与 $\lfloor {\frac{q + 1}{2}}\rfloor$ 段极长的 $1$。（将 $c_0$ 一并考虑）

至于 $k$ 的限制，经过推导得到当 $c$ 中恰好有 $k$ 个 $1$ 与 $n - k + 1$ 个 $0$（将 $c_0$ 一并考虑）时满足 $k$ 的限制。

这样一来就成了一个典型的组合数学问题了。

我们考虑将 $k$ 个 $1$ 划分为 $\lfloor {\frac{q + 1}{2}}\rfloor$ 段，将 $n - k + 1$ 个 $0$ 划分为 $\lceil {\frac{q + 1}{2}}\rceil$ 段，两者交替排列，其方案数之积即为此时合法的 $c$ 的数量。故最终有：

\[Ans = \sum \limits_{q = 0} ^ {n} {3 ^ {n - q} \cdot \binom{k - 1}{\lfloor {\frac{q + 1}{2}}\rfloor - 1} \cdot \binom{n - k}{\lceil {\frac{q + 1}{2}}\rceil - 1}} \]

i64 pp[N], fac[N];
void sieve(){
	pp[0] = 1LL; for(int i = 1; i < N; ++i) pp[i] = pp[i - 1] * 3 % mod;
	fac[0] = 1LL; for(int i = 1; i < N; ++i) fac[i] = fac[i - 1] * i % mod;
}
inline i64 ksm(i64 a, i64 b, i64 p){
	i64 ret = 1;
	while(b){
		if(b & 1) ret = ret * a % p;
		b >>= 1; a = a * a % mod;
	}
	return ret;
}
inline i64 inv(int x){return ksm(x, mod - 2, mod);}
inline i64 binom(int x, int y){
	if(y > x) return 0;
	if(y == -1) return (x == -1);
	return inv(fac[y]) * inv(fac[x - y]) % mod * fac[x] % mod;
}
void solve(){
	int n, k; cin >> n >> k;
	i64 ans = 0;
	for(int q = 0; q <= n; ++q){
		ans += pp[n - q] * binom(k - 1, (q + 1) / 2 - 1) % mod * binom(n - k, q / 2);
		ans %= mod;
	}
	cout << ans << '\n';
}

P5651 基础最短路练习题

保证 $G$ 中不存在简单环使得边权异或和不为 $0$

考虑两点间不同的最短路要么部分重合，要么部分成环，重合时异或和自然为 $0$，不重合时由于上述限制异或和也为 $0$。推广一下这个结论就知道，本题中两点间最短路的异或和一定相等，即所有路径等价。所以求一棵生成树，然后 $\mathcal{O}(n)-\mathcal{O}(1)$ 处理即可。

P2149 [SDOI2009] Elaxia的路线

$\texttt{Description}$

给定带权无向图和两对点 $(x_1,y_1),(x_2,y_2)$，求两对点间最短路的最长公共距离。

（即对于所有的 $x_1 \to y_1$ 的最短路的边集与 $x_2 \to y_2$ 的最短路的边集的交集，求这个交集的最大边权和）。

解 1

符号约定：记 $dis_{u,v}$ 表示无向图上 $u \to v$ 的最短路径长，$w_{(u,v)}$ 表示边 $(u,v)$ 的边权，最短路集指所有最短路中被包括的有向边组成的有向边集。

引理 1 一条有向边 $(u,v)$ 位于 $x \to y$ 的某条最短路上的充分必要条件是 $dis_{x,u} + w_{(u,v)} + dis_{v,y} = dis_{x,y}$。

证明利用最短路的子路径也是最短路这一性质，考虑若 $(u,v)$ 位于 $x \to y$ 的任一最短路上，则 $x \to u, v \to y$ 的部分同样是最短路；反过来，取 $x \to u, v \to y$ 的最短路径长 $dis_{x,u},dis_{v,y}$，若 $dis_{x,u} + w_{(u,v)} + dis_{v,y} = dis_{x,y}$，则有向边 $(u,v)$ 一定在一条 $x \to u \to v \to y$ 的最短路上。

引理 2 对于无向图上任意一条无向边 $(u,v)$，其所对应的两条有向边至多有 $1$ 条属于 $x \to y$ 的最短路集。

证明考虑依据边权大小建立模型：其中 $1,4$ 点为路径起止端点，$a,b$ 为非负整数，边 $(2,3)$ 的边权为 $z(z \geq 1)$，$1 \to 2, 1 \to 3, 2 \to 4, 3 \to 4$ 的最短路径长均被标注在图中。

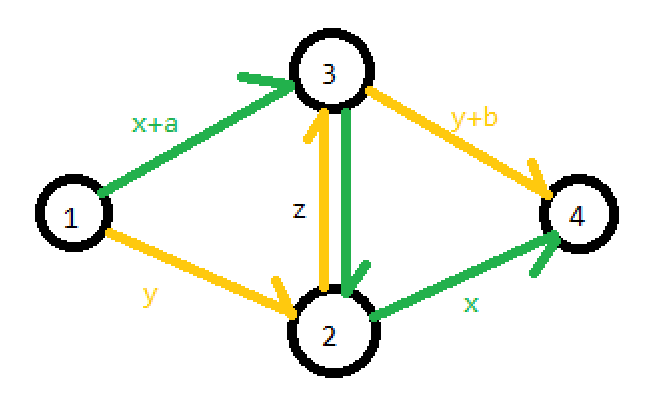
对于这种情况，有 $2$ 条可能的经过边 $(2,3)$ 或 $(3,2)$ 的路径：

$1 \to 3 \to 2 \to 4$，即绿色路径，记该路径为①
$1 \to 2 \to 3 \to 4$，即黄色路径，记该路径为②

那么，有向边 $(2,3)$ 与 $(3,2)$ 同时存在于 $1 \to 4$ 的最短路集中的充分必要条件是 $2x + a + z = 2y + b + z \leq x + y$。

解得 $x \leq y - a - z, y \leq x - b - z$。另一方面，由于 $a,b \geq 0, z \geq 1$，所以 $x,y$ 是恒无解的，所以这个关系式恒不成立，即有向边 $(2,3)$ 与 $(3,2)$ 不可能同时存在于 $1 \to 4$ 的最短路集中。

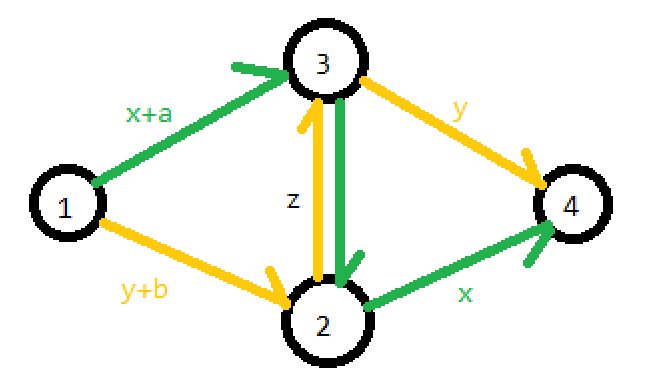
与上述讨论类似，最终仍可通过无解反证。证毕。

又由于图的边权均正整数，故最终形成的最短路集不可能出现环，因此，最短路集一定是一个DAG

引理 3 最长公共部分一定是一条链。

证明由于最短路的子路径也是最短路，所以一段公共部分上成环的部分一定可以转化为一条长度相等的链。证毕。

综上所述，我们可以求出 $x_1 \to y_1, x_2 \to y_2$ 对应的 DAG，对这两个 DAG 求最长链即可。这个过程可以对 DAG 进行一次拓扑实现，状态转移显然，$Ans_v = max{Ans_u + w_{(u,v)}} $。

大体思路是这样，但还有不少细节需要注意：（记 $x_1 \to y_1, x_2 \to y_2$ 对应的 DAG 分别为 $D_1, D_2$）

建立新图时，需要遍历每一条有向边 $(u,v)$，若 $(u,v)$ 存在于 $D_1$ 中，则考虑 $(u,v)$ 或 $(v,u)$ 是否存在于 $D_2$ 中，若存在则向一个新图中加入有向边 $(u,v)$。（由引理 2 可知这样建图 $(u,v)$ 和 $(v,u)$ 至多一者会加入新图）
按照上述规则建图，则对新图进行拓扑时 $Ans_{y_2}$ 的值不能转移到别的 $Ans_v$ 上去，即状态转移严谨来讲是这样的：

\[Ans_v = \left\{ \begin{array}{ll} w_{(u,v)}, u = y_2 \\ Ans_u + w_{(u,v)}, otherwise \end{array} \right. \]

原因在于，由于我们建立的新图中路径的方向与 $D_1$ 一致，所以新图中可能存在一条穿过 $y_2$ 的链。但是最短路到 $y_2$ 就为止了，不可能再增广到链的异侧。为了避免这个情况，因此有 $Ans_{y_2}$ 不能加到别的 $Ans_v$ 上去。

给出一份可以解释为什么不能直接转移的样例，其中 $2 \to 8, 8 \to 4, 4 \to 5$ 均为新图中存在的边，$y_2 = 8$。

至此这道题就做完了。给出完整代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1500 + 5, M = 3e5 + 5;
struct edge{
	int v, nxt, w;
}e1[M << 1], e2[M << 1];
int head1[N], tot1, head2[N], tot2, deg[N];
inline void add1(int u, int v, int w){
	e1[++tot1].nxt = head1[u];
	head1[u] = tot1;
	e1[tot1].v = v;
	e1[tot1].w = w;
}
inline void add2(int u, int v, int w){
	e2[++tot2].nxt = head2[u];
	head2[u] = tot2;
	e2[tot2].v = v;
	e2[tot2].w = w;
	++deg[v];
}
struct node{
	int val, u;
	bool operator < (const node &x) const {return val > x.val;}
};
priority_queue<node> pq;
bool vis[N];
int dis[4][N];
void dijkstra(int id, int s){
	memset(dis[id], 0x3f, sizeof(dis[id]));
	memset(vis, 0, sizeof(vis));
	dis[id][s] = 0;
	pq.push((node){0, s});
	while(!pq.empty()){
		int u = pq.top().u; pq.pop();
		if(vis[u]) continue;
		vis[u] = 1;
		for(int i = head1[u]; i; i = e1[i].nxt){
			if(dis[id][u] + e1[i].w < dis[id][e1[i].v]){
				dis[id][e1[i].v] = dis[id][u] + e1[i].w;
				pq.push((node){dis[id][e1[i].v], e1[i].v});
			}
		}
	}
}

int ans[N];
int x_1, y_1, x_2, y_2;
queue<int> S;
void topo(int n){
	for(int i = 1; i <= n; ++i) if(!deg[i]) S.push(i);
	while(!S.empty()){
		int u = S.front(); S.pop();
		for(int i = head2[u]; i; i = e2[i].nxt){
			ans[e2[i].v] = max(ans[e2[i].v], ((u == y_2)? 0 : ans[u]) + e2[i].w);
			if(--deg[e2[i].v] == 0) S.push(e2[i].v);
		}
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	int n, m; cin >> n >> m;
	 cin >> x_1 >> y_1 >> x_2 >> y_2;
	int u, v, w;
	for(int i = 1; i <= m; ++i){
		cin >> u >> v >> w;
		add1(u, v, w); add1(v, u, w);
	}
	dijkstra(0, x_1); dijkstra(1, y_1); dijkstra(2, x_2); dijkstra(3, y_2);
	for(int i = 1; i <= n; ++i){
		for(int j = head1[i]; j; j = e1[j].nxt){
			if(dis[0][i] + e1[j].w + dis[1][e1[j].v] == dis[0][y_1]){
				if(dis[2][i] + e1[j].w + dis[3][e1[j].v] == dis[2][y_2] || 
				 dis[3][i] + e1[j].w + dis[2][e1[j].v] == dis[2][y_2])
					add2(i, e1[j].v, e1[j].w);
			}
		}
	}
	topo(n);
	cout << *max_element(ans + 1, ans + n + 1);
}

解 2

建新图时其实还有一种方法：分类讨论地求一下只保留在两 DAG 中同向出现的边时的最长链，和只保留在两 DAG 中反向出现的边时的最长链。这样一来 dp 过程中就不必对 $Ans_{y_2}$ 进行特殊转移了。非常巧妙。

解 3

推广一下解 1 中的引理 2，可以得出推论：最短路算法最终形成的最短路集必然是一个 DAG。

因此，建图时除了运用解 1 中的引理 1，还有一种办法是在 $dijkstra$ 的松弛操作中记录前驱。即向松弛部分加入如下片段：

if (dis[e.to] >= e.w + dis[now.to]){
    if (dis[e.to] > e.w + dis[now.to]){
        pre[e.to].clear();
        dis[e.to] = e.w + dis[now.to];
        que.push({e.to, dis[e.to]});
    }
    pre[e.to].push_back({now.to, e.w});
}

这样一来就可以得到 $dijkstra$ 后形成的 DAG 了。但是这个 DAG 并不是我们最终想要的最短路集，因此考虑将所有的边反向后对该图进行一次 dfs，标记所有遍历到的边，这样便得到了最短路集。

P3619 魔法

考虑对于两个任务，先 $1$ 再 $2$ 的方案可行当且仅当 $T + b_1 > h_2$，即 $T > h_2 - b_1$，同理先 $2$ 后 $1$ 的方案可行当且仅当 $T > h_1 - b_2$。因此让 $h_2 - b_1 \leq h_1 - b_2$ 就能保证先 $1$ 后 $2$ 的方案一定不劣。即 $h_1 + b_1 \geq h_2 + b_2$。故按 $h_i + b_i$ 降序排序，$\mathcal{O}(n)$ 判断即可。

void solve(){
	int n; i64 T; cin >> n >> T;
	for(int i = 1; i <= n; ++i) cin >> a[i].t >> a[i].b;
	sort(a + 1, a + n + 1);
	for(int i = 1; i <= n; ++i){
		if(T <= a[i].t){
			cout << "-1s\n";
			return;
		}
		T += a[i].b;
		if(T <= 0){
			cout << "-1s\n";
			return;
		}
	} 
	cout << "+1s\n";
}

P3953 [NOIP2017 提高组] 逛公园

记 $dis_{u \to v}$ 表示 $u \to v$ 的最短路径长，$w(u,v)$ 表示有向边 $(u,v)$ 的权值。

当图上有 $0$ 环且经过该 $0$ 环的方案数不为 $0$ 时方案数无穷。给出两种方法：

在 $dp$ 过程中记一个 $instack$。
对 $0$ 边建图跑 $dfs$，判断是否存在 $0$ 环使得 $0$ 环上存在一边 $(u,v)$ 使 $dis_{1 \to u} + dis_{v \to n} \leq dis_{1 \to n} + k$。

由于一条路径大于最短路的增量一定是在路径中逐渐增大的，因此考虑设计一种无后效性的 $dp$：记 $dp(u,k)$ 表示 $1 \to u$ 的长度为 $dis_{1 \to u} + k(k \geq 0)$ 的路径数，则状态转移是容易的：

\[dp(v,k) = \sum \limits_{(u,v) \in E} {dp(u, dis_{1 \to v} + k - w(u,v) - dis_{1 \to u})} \]

不难知道 $dis_{1 \to v} + k - w(u,v) - dis_{1 \to u} \leq k$，而当这个值为负时显然对应的方案数为 $0$（不可能有比最短路还短的路径）。拓扑排序后 dp 或直接记忆化搜索即可。（代码判 $0$ 环的方式是记录 $instack$)

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 1e5 + 10, M = 2e5 + 10, INF = 1e9;
struct edge{
	int v, nxt, w;
}e1[M], e2[M];
int head1[N], head2[N], tot1, tot2;
inline void add1(int u, int v, int w){
	e1[++tot1].nxt = head1[u];
	head1[u] = tot1;
	e1[tot1].v = v;
	e1[tot1].w = w;
}
inline void add2(int u, int v, int w){
	e2[++tot2].nxt = head2[u];
	head2[u] = tot2;
	e2[tot2].v = v;
	e2[tot2].w = w;
}
struct node{
	int val, u;
	bool operator < (const node &x) const {return val > x.val;}
};
priority_queue<node> pq;
bool vis[N];
int dis[N];
int n, m, p;
void dijkstra(int s){
	for(int i = 1; i <= n; ++i) vis[i] = 0, dis[i] = INF;
	dis[s] = 0;
	pq.push((node){0, s});
	while(!pq.empty()){
		int u = pq.top().u; pq.pop();
		if(vis[u]) continue;
		vis[u] = 1;
		for(int i = head1[u]; i; i = e1[i].nxt){
			if(dis[e1[i].v] > dis[u] + e1[i].w){
				dis[e1[i].v] = dis[u] + e1[i].w;
				pq.push((node){dis[e1[i].v], e1[i].v});
			}
		}
	}
}
bool ins[N][60], fail;
int f[N][60];
int dp(int v, int k){
	if(fail) return 0;
	if(k < 0) return 0;
	if(ins[v][k]){
		fail = 1;
		return 0;
	}
	if(f[v][k] != -1) return f[v][k];
	ins[v][k] = 1;
	int ans = 0;
	for(int i = head2[v]; i && !fail; i = e2[i].nxt)
		ans = (ans + dp(e2[i].v, dis[v] + k - e2[i].w - dis[e2[i].v])) % p;
	if(v == 1 && k == 0) ans = (ans + 1) % p;
	ins[v][k] = 0;
	return f[v][k] = ans;
}
void solve(){
	int K; cin >> n >> m >> K >> p;
	tot1 = tot2 = 0;
	for(int i = 1; i <= n; ++i){
		head1[i] = head2[i] = 0;
		for(int j = 0; j <= K; ++j) ins[i][j] = 0, f[i][j] = -1;
	}
	int u, v, w;
	for(int i = 1; i <= m; ++i){
		cin >> u >> v >> w;
		add1(u, v, w);
		add2(v, u, w);
	}
	dijkstra(1);
	fail = 0;
	int res = 0;
	for(int i = 0; i <= K; ++i){
		res = (res + dp(n, i)) % p;
		if(fail){
			cout << "-1\n";
			return;
		}
	}
	cout << res << '\n';
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	int T; cin >> T;
	while(T--) solve();
}

UVA12620 Fibonacci Sum

斐波那契数列在取模意义下是有循环节的（详细证明），一个结论是在模 $p$ 意义下，循环节的大小不会大于 $6p$。因此直接 $\mathcal{O}(n^2)$ 判断或打表即可。对于该题结论为每 $300$ 项为一循环节。

inline void query(i64 l, i64 r){
	i64 n = r / 300 - (l + 299) / 300;
	i64 ans = n * s[300];
	ans += s[300] - s[(l - 1) % 300];
	ans += s[((r - 1) % 300 + 1) % 300];
	cout << ans << '\n';
}

P4366 [Code+#4]最短路

有一定思维的图论题。

直接加边作完全图一定会炸，考虑怎么将路径转化为等价的路径。我们发现贡献中这个 $(i~\mathrm{xor}~j)$ 的形式可以拆成从 $i$ 到 $j$ 一位一位修改，这启示我们对于每一个点 $i$，只需连 $i \to (i~\mathrm{xor}~2^k)$ 的有向边即可覆盖所有情况。此时路径的权值显然是 $2^k \times C$。

这样的边数是 $\mathcal{O}(m + n \log n)$ 的，总复杂度 $\mathcal{O}(n \log (m + n\log n))$。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 3e6 + 10;
struct edge{
	int v, nxt, w;
}e[M];
int head[N], tot;
inline void add(int u, int v, int w){
	e[++tot].nxt = head[u];
	head[u] = tot;
	e[tot].v = v;
	e[tot].w = w;
}
struct node{
	int val, u;
	bool operator < (const node &x) const {return val > x.val;}
};
priority_queue<node> pq;
bool vis[N];
int dis[N];
void dijkstra(int s){
	memset(dis, 0x3f, sizeof(dis));
	dis[s] = 0;
	pq.push((node){0, s});
	while(!pq.empty()){
		int u = pq.top().u; pq.pop();
		if(vis[u]) continue;
		vis[u] = 1;
		for(int i = head[u]; i; i = e[i].nxt){
			if(dis[e[i].v] > dis[u] + e[i].w){
				dis[e[i].v] = dis[u] + e[i].w;
				pq.push((node){dis[e[i].v], e[i].v});
			}
		}
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	int n, m, C; cin >> n >> m >> C;
	int u, v, w;
	for(int i = 1; i <= m; ++i){
		cin >> u >> v >> w;
		add(u, v, w);
	}
	int to;
	for(int i = 0; i <= n; ++i){
		for(int j = 0; j <= 20; ++j){
			to = i ^ (1 << j);
			if(to <= n) add(i, i ^ (1 << j), (1 << j) * C);
		}
	}
	cin >> u >> v;
	dijkstra(u);
	cout << dis[v];
}