526互联

强化学习基础篇【1】：基础知识点、马尔科夫决策过程、蒙特卡洛策略梯度定理、REINFORCE 算法

发布时间 2023-06-02 13:51:01作者: 汀、人工智能

强化学习基础篇【1】：基础知识点、马尔科夫决策过程、蒙特卡洛策略梯度定理、REINFORCE 算法

1.强化学习基础知识点

智能体（agent）：智能体是强化学习算法的主体，它能够根据经验做出主观判断并执行动作，是整个智能系统的核心。

环境（environment）：智能体以外的一切统称为环境，环境在与智能体的交互中，能被智能体所采取的动作影响，同时环境也能向智能体反馈状态和奖励。虽说智能体以外的一切都可视为环境，但在设计算法时常常会排除不相关的因素建立一个理想的环境模型来对算法功能进行模拟。

状态（state）：状态可以理解为智能体对环境的一种理解和编码，通常包含了对智能体所采取决策产生影响的信息。

动作（action）：动作是智能体对环境产生影响的方式，这里说的动作常常指概念上的动作，如果是在设计机器人时还需考虑动作的执行机构。

策略（policy）：策略是智能体在所处状态下去执行某个动作的依据，即给定一个状态，智能体可根据一个策略来选择应该采取的动作。

奖励（reward）：奖励是智能体贯式采取一系列动作后从环境获得的收益。注意奖励概念是现实中奖励和惩罚的统合，一般用正值来代表奖励，用负值代表实际惩罚。
:

在flappy bird游戏中，小鸟即为智能体，除小鸟以外的整个游戏环境可统称为环境，状态可以理解为在当前时间点的游戏图像。在本游戏中，智能体可以执行的动作为向上飞，或什么都不做靠重力下降。策略则指小鸟依据什么来判断是要执行向上飞的动作还是什么都不做，这个策略可能是根据值函数大小判断，也可能是依据在当前状态下执行不同动作的概率或是其他的判断方法。奖励分为奖励和惩罚两种，每当小鸟安全的飞过一个柱子都会获得一分的奖励，而如果小鸟掉到地上或者撞到柱子则或获得惩罚。

2.马尔科夫决策过程

图1: 经典吃豆人游戏

在经典的吃豆人游戏中，吃豆人通过对环境进行观察，选择上下左右四种动作中的一种进行自身移动，吃掉豆子获得分数奖励，并同时躲避幽灵防止被吃。吃豆人每更新一次动作后，都会获得环境反馈的新的状态，以及对该动作的分数奖励。在这个学习过程中，吃豆人就是智能体，游戏地图、豆子和幽灵位置等即为环境，而智能体与环境交互进行学习最终实现目标的过程就是马尔科夫决策过程（Markov decision process，MDP）。

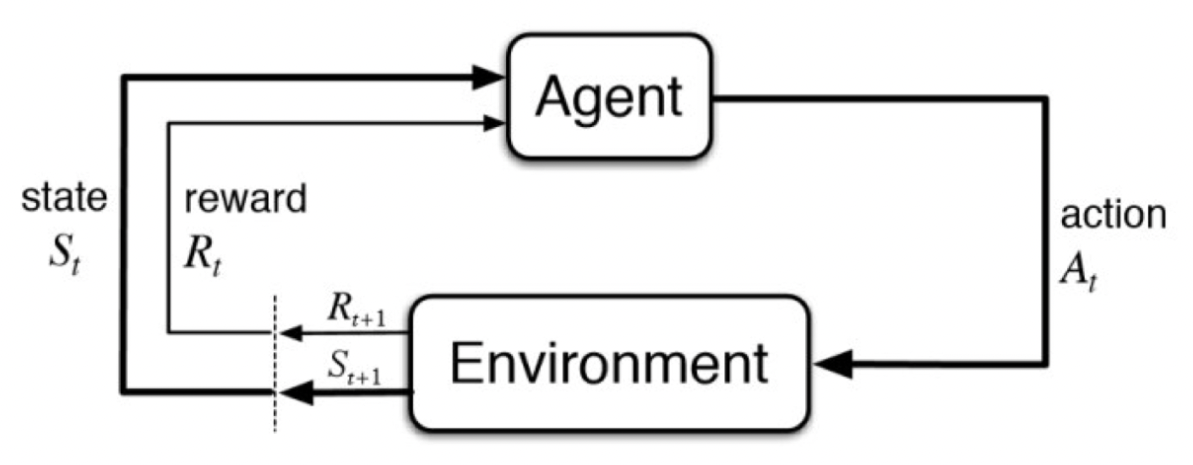
图2: 马尔科夫决策过程中的智能体-环境交互

上图形式化的描述了强化学习的框架，智能体（Agent）与环境（Environment）交互的过程：在 $t$ 时刻，智能体在当前状态 $S_t$ 采取动作 $A_t$。在下一时刻 $t+1$，智能体接收到环境反馈的对于动作 $A_t$ 的奖励 $R_{t+1}$，以及该时刻状态 $S_{t+1}$。从而，MDP和智能体共同给出一个轨迹：

$$
S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,S_3,A_3,...
$$
接下来，更具体地定义以下标识：

  • $S_t$ 是有限的状态集合
  • $A_t$ 是有限的动作集合
  • $P$ 是基于环境的状态转移矩阵：其中每一项为智能体在某个状态 $s$ 下，采取动作 $a$ 后，与环境交互后转移到其他状态 $s^{'}$ 的概率值，表示为 $P(S_{t+1}=s^{'}|s_{t}=s,a_{t}=a)$
  • R是奖励函数：智能体在某个状态 $s$ 下，采取动作 $a$ 后，与环境交互后所获得的奖励，表示为 $R(s_{t}=s,a_{t}=a)$
  • $\gamma$ 是折扣因子(discounted factor)，取值区间为 $[0,1]$

所以MDP过程可以表示为 $(S,A,P,R,\gamma)$，如果该过程中的状态转移矩阵 $P$ 和奖励 $R(s,a)$ 对智能体都是可见的，我们称这样的Agent为Model-based Agent，否则称为Model-free Agent。

3.策略梯度定理

策略函数的参数化可表示为$\pi_{\theta}(s,a)$，其中$\theta$为一组参数，函数取值表示在状态$s$下选择动作$a$的概率。为了优化策略函数，首先需要有一个对策略函数优劣进行衡量的标准。假设强化学习问题的初始状态为$s_{0}$，则希望达到最大化的目标为

$$
J(\theta) := V_{\pi_{\theta}}(s_{0})
$$
其中，$v_{\pi_{\theta}}$是在策略$\pi_{\theta}$下的真实价值函数，这个价值函数代表衡量一个状态的价值，即一个状态采取所有行为后的一个价值的期望值。如果能求出梯度$\nabla_{\theta}J(\theta)$，就可以用梯度上升法求解这个问题，即求解价值函数的最大值。

在这个函数中，$J(\theta)$既依赖于动作的选择有依赖于动作选择时所处状态的分布。给定一个状态，策略参数对动作选择及收益的影响可以根据参数比较直观地计算出来，但因为状态分布和环境有关，所以策略对状态分布的影响一般很难确切知道。而$J(\theta)$对模型参数的梯度却依赖于这种未知影响，那么如何估计这个梯度呢？

Sutton等人在文献中给出了这个梯度的表达式：

$$
\nabla_{\theta}J(\theta)\propto\sum_{s}\mu_{\pi_{\theta}}(s)\sum_{a}q_{\pi_{\theta}}(s,a)\nabla_{\theta}\pi_{\theta}(s,a)
$$
其中，$\mu_{\pi_{\theta}}(s)$称为策略$\pi_{\theta}$的在策略分布。在持续问题中，$\mu_{\pi_{\theta}}(s)$为算法$s_{0}$出发经过无限多步后位于状态$s$的概率。

策略梯度定理的证明：（注意：在证明过程中，为使符号简单，我们在所有公式中隐去了$\pi$对$\theta$的依赖）

$$
\scriptsize{
\begin{align}
\nabla v_{\pi}(s) &= \nabla[\sum_{a}\pi(a|s)q_{\pi}(s,a) \
&= \sum_{a}[\nabla\pi(a|s)q_{\pi}(s,a)+\pi(a|s)\nabla q_{\pi}(s,a)] \
&= \sum_{a}[\nabla\pi(a|s)q_{\pi}(s,a)+\pi(a|s)\nabla\sum_{s{'},r}p(s,r|s,a)(r+v_{\pi}(s^{'}))] \
&= \sum_{a}[\nabla\pi(a|s)q_{\pi}(s,a)+\pi(a|s)\sum_{s{'}}p(s|s,a)\nabla v_{\pi}(s^{'})] \
&= \sum_{a}[\nabla\pi(a|s)q_{\pi}(s,a)+\pi(a|s)\sum_{s{'}}p(s|s,a)\sum_{a{'}}[\nabla\pi(a|s{'})q_{\pi}(s,a{'})+\pi(a|s{'})\sum_{s{''}}p(s{''}|s,a^{'})\nabla v_{\pi}(s^{''})]] \
&= \sum_{s \in S}\sum_{k=0}^{\infty}Pr(s\rightarrow x,k,\pi)\sum_{a}\nabla\pi(a|x)q_{\pi}(x,a)
\end{align}}
$$
其中，$Pr(s\rightarrow x,k,\pi)$是在策略$\pi$下，状态$s$在$k$步内转移到状态$x$的概率。所以，我们可以得到：

$$
\begin{align}
\nabla J(\theta) &= \nabla v_{\pi}(s_{0}) \
&= \sum_{s}(\sum_{k=0}^{\infty}Pr(s_{0}\rightarrow s,k,\pi))\sum_{a}\nabla\pi(a|s)q_{\pi}(s,a) \
&= \sum_{s}\eta(s)\sum_{a}\nabla\pi(a|s)q_{\pi}(s,a) \
&= \sum_{s{'}}\eta(s)\sum_{s}\frac{\eta(s)}{\sum_{s{'}}\eta(s)}\sum_{a}\nabla\pi(a|s)q_{\pi}(s,a) \
&= \sum_{s{'}}\eta(s)\sum_{s}\mu(s)\sum_{a}\nabla\pi(a|s)q_{\pi}(s,a) \
&\propto\sum_{s}\mu(s)\sum_{a}\nabla\pi(a|s)q_{\pi}(s,a)
\end{align}
$$

4.蒙特卡洛策略梯度定理

根据策略梯度定理表达式计算策略梯度并不是一个简单的问题，其中对$\mu_{\pi_{\theta}}$和$q_{\pi_{\theta}}$的准确估计本来就是难题，更不要说进一步求解$\nabla_{\theta}J(\theta)$了。好在蒙特卡洛法能被用来估计这类问题的取值，因此首先要对策略梯度定理表达式进行如下的变形：

$$
\begin{align}
\nabla_{\theta}J(\theta) &\propto\mu_{\pi_{\theta}}(s)\sum_{a}q_{\pi_{\theta}}(s,a)\nabla_{\theta}\pi_{\theta}(s,a) \
&= \sum_{s}\mu_{\pi_{\theta}}(s)\sum_{a}\pi_{\theta}(s,a)[q_{\pi_{\theta}}(s,a)\frac{\nabla_{\theta}\pi_{\theta}(s,a)}{\pi_{\theta}(s,a)}] \
&= \mathbb{E}{s, a\sim\pi}[q{\pi_{\theta}}(s,a)\frac{\nabla_{\theta}\pi_{\theta}(s,a)}{\pi_{\theta}(s,a)}] \
&= \mathbb{E}{s, a\sim\pi}[q{\pi_{\theta}}(s,a)\nabla_{\theta}\ln{\pi_{\theta}(s,a)}]
\end{align}
$$
上式为梯度策略定理的一个常见变形，但由于式中存在$q_{\pi_{\theta}}$，算法无法直接使用蒙特卡洛法来求取其中的期望。为此，进一步将该式进行变形，得到：

$$
\begin{align}
\nabla_{\theta}J(\theta) &\propto\mathbb{E}{s, a\sim\pi}[\mathbb{E}[G_{t}|s,a]\nabla_{\theta}\ln{\pi_{\theta}(s,a)}] \
&= \mathbb{E}{s, a\sim\pi}[G\nabla_{\theta}\ln{\pi_{\theta}(s,a)}]
\end{align}
$$
其中，$T(s,a)$表示从状态$s$开始执行动作$a$得到的一条轨迹（不包括$s$和$a$），$G_{t}$为从状态$s$开始沿着轨迹$T(s,a)$运动所得的回报。可以使用蒙特卡洛采样法来求解（即上述公式），算法只需要根据策略来采样一个状态$s$、一个动作$a$和将来的轨迹，就能构造上述公式中求取期望所对应的一个样本。

5.REINFORCE 算法

REINFORCE （蒙特卡洛策略梯度） 算法是一种策略参数学习方法，其中策略参数 $\theta$ 的更新方法为梯度上升法，它的目标是为了最大化性能指标 $J(\theta)$ , 其更新公式为：

$$
\theta_{t+1} = \theta_{t} + \alpha\widehat{\nabla J(\theta_t)}
$$
根据蒙特卡洛定理中对 $\nabla_{\theta}J(\theta)$ 的计算，则有：

$$
\nabla_{\theta}J(\theta) = \mathbb{E}{s, a\sim\pi}[G\nabla_{\theta}\ln{\pi_{\theta}(s,a)}]
$$
根据上述梯度更新公式， 得到蒙特卡洛策略梯度更新公式：

$$
\theta = \theta + \eta\gamma^{'} G\nabla_\theta\ln\pi_\theta(s_t, a_t)
$$
其中，$\eta$ 为学习率，$\gamma^{'}$ 为衰减率，在REINFORCE算法中，暂不考虑衰减问题，设置 $\gamma^{'} = 1$ 。

REINFORCE 算法流程：

输入：马尔可夫决策过程$MDP=(S, A, P, R, \gamma)$，即状态，智能体，决策，奖励和折现系数，$\gamma = 1$，暂不讨论。
输出：策略 $\pi(a|s, \theta)$，即在状态为s，参数为$\theta$的条件下，选择动作a的概率。
算法的具体流程：

  1. 随机初始化；
  2. repeat
  3. 根据策略$\pi_\theta$采样一个片段(episode，即智能体由初始状态不断通过动作与环境交互，直至终止状态的过程)，获得$s_0, a_0, R_1, s_1, ..., s_T-1, a_T-1, R_T$；
    2. for $t \leftarrow 0$ to $T - 1$ do
    1. $G \leftarrow \sum_{k=1}^{T-t} \gamma_{k-1} R_{t+k}$，G是对回报的计算，回报是奖励随时间步的积累，在本实验中，$\gamma = 1$。
      2. $\theta = \theta + \eta\gamma^{'} G\nabla_\theta\ln\pi_\theta(s_t, a_t)$，其中$\eta$是学习率。策略梯度算法采用神经网络来拟合策略梯度函数，计算策略梯度用于优化策略网络。
  4. 直到$\theta$收敛

更多文章请关注公重号：汀丶人工智能