526互联

P9476 [_-0 B] 地铁

发布时间 2023-09-26 08:53:51作者: FOX_konata

原题

人类智慧题！！！

假如没有地铁，这题就是一个非常典型的计算贡献的题。我们对每一条边看他左右子树中通过的客流量多少，对于一个边权为 \(w\) 的边，他的贡献显然为 \(w \times S_1 \times S_2\) ，其中 \(S_1,S_2\) 为当前边把树分成左右两部分的子树大小

现在有了地铁，使答案减少了 \(D\)

假设一个人从 \(A\) 走到 \(B\) ，路经 \(A,p_1,p_2,...,p_t,B\) 共 \(t+2\) 个点，则对 \(D\) 产生的贡献是：

\[(w_{A \rightarrow p_1}-w'_{A \rightarrow p_1}) + (w_{p_1 \rightarrow p_2}-w'_{p_1 \rightarrow p_2}) + ... +(w_{p_t \rightarrow B}-w'_{p_t \rightarrow B})-t \]

这个式子中的 \(t\) 看起来非常碍眼，因为我们想要考虑每个边对答案产生的贡献，但 \(t\) 显然与每条边无关，而是和这个人有没有经过铁路有关，这是我们不想要的，因此我们可以魔改一下式子：

\[(w_{A \rightarrow p_1}-w'_{A \rightarrow p_1}-t)+t + (w_{p_1 \rightarrow p_2}-w'_{p_1 \rightarrow p_2}-t)+t + ... +(w_{p_t \rightarrow B}-w'_{p_t \rightarrow B}-t) \]

这样看起来就好多了，因为 \(w - w' - t\) 就可以看成是路径上边的贡献，而 \(t\) 就可以看成是路径上度数为 \(2\) 的点的贡献(即把所有点的点权都看成 \(t\))

因此我们考虑每个边和每个点贡献的次数

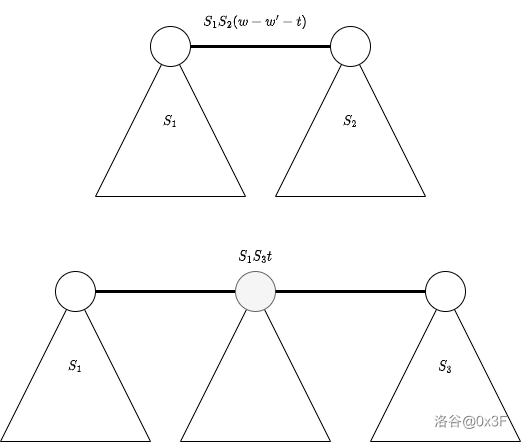
对于一条边，计算同上，对 \(D\) 的贡献为 \((w - w' - t) \times S_1 \times S_2\)

对于一个点，他把树分成了三个部分，如图，他的贡献为 \(t \times S_1 \times S_3\)

因此我们考虑树形 \(dp\)

设 \(dp_i\) 表示以 \(i\) 为根的子树中，链的一端为 \(i\) 的父亲，另一端在 \(i\) 的子树中的最大贡献

我们发现转移分两种情况：

  1. 链的另一端就是 \(i\) 点
    此时 \(dp_i \leftarrow (w_{(i,fa_i)} - w'_{(i,fa_i)}-t) \times siz_i \times (N - siz_i)\)

  2. 链的另一端在 \(j\) 点的子树内，其中 \(j\) 是 \(i\) 的直接儿子
    此时 \(dp_i \leftarrow (w_{(i,fa_i)} - w'_{(i,fa_i)} - t) \times siz_i \times (N - siz_i) + t \times siz_j \times (N - siz_i) + dp_j\)

在求完 \(dp\) 值后还没完，因为我们还没有找到答案，我们要考虑怎么更新答案。不妨设最终答案为 \(D\)

我们设地铁两个端点的 \(LCA\) 为 \(r\) ，则有两种可能：

  1. 如果 \(r\) 是端点，则 \(D \leftarrow dp_r\)

  2. 如果 \(r\) 不是端点，则 \(D \leftarrow dp_s + dp_t + t \times siz_s \times siz_t\)

注意，这里读入的 \(t\) 和铁路的端点 \(t\) 并不是一个 \(t\) ！

对于第一种情况是很好考虑的，直接对于每个点更新一边 \(D\) 即可

但对于第二种情况，我们直接枚举 \(s,t\) 显然会超时，怎么办呢

我们再次考虑魔改一下式子：

\[D - dp_s = t \times siz_t \times siz_s + dp_t \]

这长的想什么？像斜率优化！

\(y : dp_t\)
\(x : -t \times siz_t\)
\(k : siz_s\)
\(b : D - dp_s\)

我们可以把他们按照 \(siz\) 排个序，然后用单调队列维护凸包

最终复杂度 \(O(n \log n)\) ，瓶颈在于排序