理解很困难,但是代码真的很简单。祝贺我过了我做的第一个有关置换的题目。
problem
已经不是能简化的东西了
一位科学家正在研究一个自我生长的长度为 \(n\) 的排列 \(a_1,a_2,\ldots,a_n\)。
排列每天都会变化,每一天,元素 \(x\) 都会变成 \(a_x\),即 \(a_x\) 会变成 \(a_{a_x}\)。具体地:
- 第一天,排列会变成 \(b\),其中 \(b_x = a_{a_x}\);
- 第二天,排列会变成 \(c\),其中 \(c_x = b_{b_x}\);
- \(\ldots\)
例如,若 \(a = [2,3,1]\),则第一天会变成 \([3,1,2]\),第二天会变成 \([2,3,1]\)。
定义 \(\sigma(x) = a_x\),定义 \(f(x)\) 为最小的正整数 \(m\) 满足 \(\sigma^m(x) = x\),其中 \(\sigma^m(x) = \underbrace{\sigma(\sigma(\ldots \sigma}_{m \text{ 个 } \sigma}(x) \ldots))\)。
例如,\(a = [2,3,1]\) 时,\(\sigma(1) = 2\),\(\sigma^2(1) = \sigma(\sigma(1)) = \sigma(2) = 3\),\(\sigma^3(1) = \sigma(\sigma(\sigma(1))) = \sigma(3) = 1\),故 \(f(1) = 3\)。再例如 \(a = [4,2,1,3]\),\(\sigma(2) = 2\) 故 \(f(2) = 1\);\(\sigma(3) = 1\),\(\sigma^2(3) = 4\),\(\sigma^3(3) = 3\) 故 \(f(3) = 3\)。
现在给出第 \(k\) 天的排列 \(a'\)。求找出一个初始的排列 \(a\) 使得 \(\sum\limits^n_{i=1} \dfrac{1}{f(i)}\) 最小。
\(1 \le n \le 2 \cdot 10^5\),\(1 \le k \le 10^9\)
solution
置换
置换:一个排列 \(A=\{A_1,A_2,\cdots,A_n\}\)。
定义两个置换的乘法 \(A\times B\) 为一个新的置换为 \(\{B_{A_1},B_{A_2},\cdots,B_{A_n}\}\)。单位元是 \(\{1,2,\cdots,n\}\)。
对置换建一个图:\(i\to p_i\)。一次开平方就变成 \(i\to p_{p_i}\),也就是这个图往前走两步的结果。
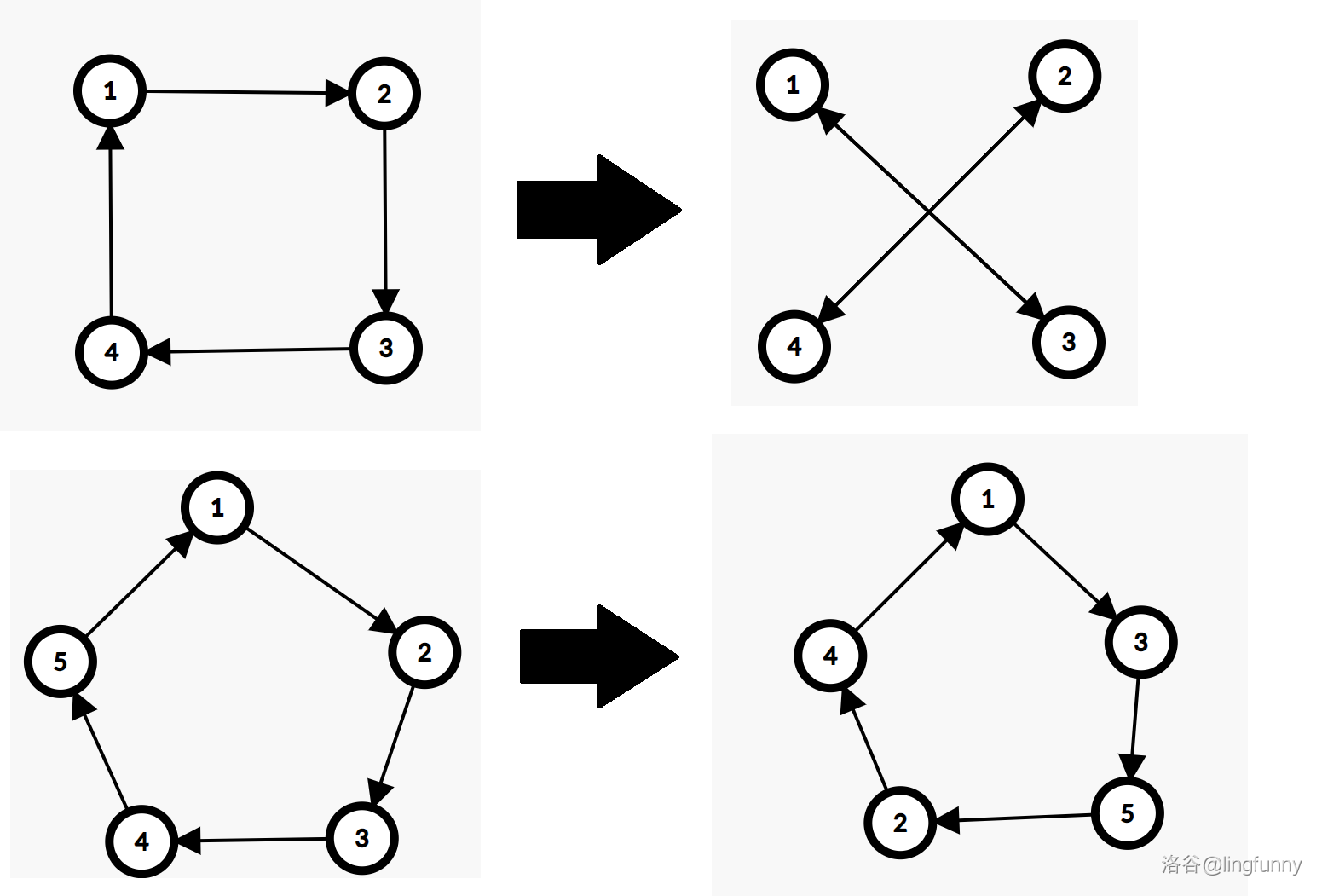
(图源:https://www.luogu.com.cn/blog/_post/546969)
可以定义置换环:原图上这些有向环就叫置换环,一个置换可能有很多个环。(注意到每个点的入度和出度都为一)。
下面是一个性质:对于长度为 \(n\) 的置换环 \(A\),\(A^k\) 是 \(\gcd(n,k)\) 个长度相等置换环拼起来的结果。
证明:考虑在环上走。。。
这里注意一下,原题中的操作是 \(a'=a^{(2^k)}\)(开 \(k\) 次平方)而不是 \(a^k\)(对着 \(a\) 用 \(a\) 做 \(k-1\) 次置换)。
时间正流
考虑初始的 \(a\),有好多好多好多个环!!!
对于一个环我们把它拉出来记为 \(c\)(就是按照顺序遍历环),然后我们说:经过 \(k\) 天后,\(c_i\) 会指向 \(c_{(i+2^k)\bmod n}\) 的地方。所以我们可以写 SPJ 了!
然后的话,对于一个偶环,经过一天后会被拆成两个环;而对于奇环则不会。
然后考虑 \(f(i)\) 是什么,其实是置换环长度,也就是说 \(\sum_i f(i)\) 就是 \(a\) 中置换环个数。
对着置换环开根号
考虑一个小一点的问题:已知 \(A^2=B\),给出 \(B\) 求 \(A\)。
先把算法流程写出来:
- 定义指针 \(i=j=1\),辅助数组 \(c\)。
- \(c_j=B_i\)。
- \(j=j+2\),\(p=B_p\)。
- 如果 \(c\) 没被填满,回到第二步;否则去往第五步。
- \(ans_{c_i}=c_{(i+1)\bmod n}\)
example:
b: 3 1 4 5 2
c: 3 2 4 1 5
a: 5 4 2 1 3
我们冷静一下,这实际上是还原了原来置换环的样子。我们同时说明了这个 \(A\) 不是惟一的。
时间倒流
为了使 \(a\) 中置换环个数尽可能少,我们考虑合并很多个环。
对于 \(a'\) 中的长度相同的偶环,因为偶环再变换一个还能再拆(其实最多拆 \(\log\) 次),说明这些偶环是恰好活到这里。
这就说明我们在 \(a\) 中的大偶环最终拆成了 \(2^k\) 个小的。所以合并的时候也是 \(2^k\) 个偶环拼在一起(注意这个是可以同步进行的,但必须是 \(2^k\) 个合并)。如果 \(k\) 很大,可以报无解了。
对于 \(a'\) 中的长度相同的奇环,可以合并,也可以不合并,反正都那样。
为了贪心,我们从大到小枚举 \(j=20\to 0\) 合并 \(2^j\) 个奇环。
有一个问题:怎么合并呢?这和手撕根号一样,还是还原置换环的原始形态,只不过现在是一堆置换环要拼在一起了。
做完了。
code
点击查看代码
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
struct Impossible{};
LL qpow(LL a,LL b,int p=1e9){LL r=1;for(a%=p;b;b>>=1,a=a*a%p) if(b&1) r=r*a%p; return r;}
int n,m,dest[1<<17];
vector<int> cyc[1<<17],buc[1<<17];
bool vis[1<<17];
void findcycle(){
for(int i=1;i<=n;i++){
if(vis[i]) continue;
int p=i; cyc[i].push_back(i);
while(dest[p]!=i) cyc[i].push_back(p=dest[p]),vis[p]=1;
buc[cyc[i].size()].push_back(i);
}
}
int mian(){
for(int i=1;i<=n;i++) scanf("%d",dest+i);
findcycle();
int lim=qpow(2,min(m,20));
try{
for(int siz=0;siz<=n;siz++){
int len=buc[siz].size();
if(siz%2==0&&len%lim) throw Impossible();
for(int T=lim;T>=1;T>>=1){
int Tsiz=T*siz;
while(len>=T){
vector<int> tmp(Tsiz);
for(int i=len-T;i<len;i++){
int j=i-len+T;
for(auto&p:cyc[buc[siz][i]]) tmp[j]=p,j=(j+qpow(2,m,Tsiz))%Tsiz;
}
for(int j=0;j<T*siz;j++) dest[tmp[j]]=tmp[(j+1)%Tsiz];
len-=T;
}
}
}
puts("YES");
for(int i=1;i<=n;i++) printf("%d%c",dest[i]," \n"[i==n]);
}catch(Impossible){puts("NO");}
return 0;
}
void reset(){
for(int i=1;i<=n;i++) cyc[i].clear(),buc[i].clear(),vis[i]=0;
}
int main(){
// #ifdef LOCAL
// freopen("input.in","r",stdin);
// #endif
for(scanf("%*d");~scanf("%d%d",&n,&m);reset(),mian());
return 0;
}