我们已经知道,GAN使用的损失函数为特殊的二进制交叉熵函数(BCE Loss),公式常写作
但是,这其中的 \(\mathop{min} \limits_G \mathop{max} \limits_D\) 有着什么样的含义?在吴恩达生成对抗神经网络的课程中所提到的生成器想要“最大化”损失,判别器想要“最小化”损失,为什么在这个公式中刚好又是相反的?你可能会说,吴恩达课程中的交叉熵前面有个负号,那么这个负号是为什么会出现在前面?
首先我们先不看公式,先来看看吴恩达课程中是怎么描述这个最大最小博弈的。
生成器想要最大化损失函数,因为这意味着鉴别器表现不佳,并且其将假值判定为真值。判别器想要最小化损失函数,因为这意味着它正确的分类的图像。
讲人话,对于生成器来讲,生成的图像能够使得判别器判断不出真假,达到以假乱真的效果,那么生成器的目的就达到了。而对于判别器来讲,判别器当然希望自己越能分辨出图片的真假越好。这段话没毛病,但是好像跟我们的 \(\mathop{min} \limits_G \mathop{max} \limits_D\) 所违背?那我们来再仔细看眼这个公式。
我们先将公式分解一下,把交叉熵这个损失函数单独提取出来,即
该式表示为,全部\(m\)个样本的交叉的均值(因为当真实数据和生成数据的样本点固定下来时,期望\(\mathbb{E}\)就等于均值)。在式中,\(x_i\)代表真实数据,\(z_i\)代表和真实数据相同结构的潜在噪声,也就是随机数据。则\(G(z_i)\)表示在生成器(Generator)中基于\(z_i\)生成的假数据,而\(D_i\)则表示判别器(Discriminator)在真实数据\(x_i\)上的判断结果,进一步\(D(G(z_i))\)则表示为判别器在生成器的假数据上的判断结果。其中,这两个结果都是基于“真”来讲的,即\(D(x_i)\)与\(D(G(z_i))\)都是样本为真(标签为1)的概率。
那么,看到了这个式子中,这么多的\(log\)函数,我们直接想到其函数图
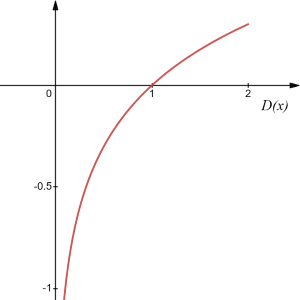
通过函数图,我们更能够清晰看到,该函数是一个单调递增的函数。结合上面所描述的,\(D(x_i)\)与\(D(G(z_i))\)既然描述的都是样本为真的概率,那么其取值应当为\([0, 1]\),那么\(log\)函数在定义域\([0, 1]\)区间内,取值则应当为\((-\infty,0)\)。换句话说,在损失函数\(V\)上不存在最小值,只存在最大值。
根据上述结论,可以总结出:当\(logD(x_i)\)最大(即将真实数据判别为真),并且\(log(1-D(G(z_i)))\)最大时(即将假数据判断为假),损失函数达到最大值。即损失\(V\)在判别器的判别能力最强时达到最大值。那这个结论不就是说判别器判的越准确,损失越大?这好像违背我们“损失函数”这个词的意思。那么我们再从判别器和生成器两个角度来看下这个问题。
对于判别器来讲,判别器都需要判断真实数据和生成数据,也就是损失函数\(V\)的前半部分和后半部分都与其有关联。那么对于判别器的损失在数学形式上和函数\(V\)是一致的,我们用\(Loss_D\)来表示判别器的损失,则有
而对于生成器来讲,生成器无法影响\(D(x_i)\),因此只需要关注函数\(V\)的后半部分,我们用\(Loss_G\)来表示生成器的损失,则有
假如我们是一个收古董的中介,我们肯定希望自己有一双火眼金睛,可以一眼看出卖家给我们的画作是不是真迹,或者当我们无法确认的时候,我们给别人说“你的收藏品八成是真的”。这时我们就相当于判别器,希望自己判断尽量准确的同时,输出“为真的概率”。在带入\(Loss_D\)后,最佳的损失值则是
这说明判别器希望最大化\(Loss_D\),并且理论上限是0,其本质是令\(D(x_i)\)逼近1,\(D(G(z_i)))\)逼近0。
假如我们是个专业古董造假团队,我们肯定希望自己造出来的东西越真越好,最好真的连顶尖仪器都扫描不出来,因此这时候我肯定希望我的\(D(G(z_i))\)是无限接近1的,也就是让判别器判断我的东西就是真的。在带入\(Loss_G\)后,最佳损失值则是
这说明生成器希望最小化\(Loss_G\),并且理论下限是无穷小,其本质是令\(D(x_i)\)逼近1,\(D(G(z_i)))\)逼近0。
由此,通过共享损失函数\(V\),判别器与生成器实现了互相对抗,也就是我们所说的最大最小博弈,即 \(\mathop{min} \limits_G \mathop{max} \limits_D\) 。只要训练过程很顺利,那么\(D(x_i)\)与\(D(G(z_i)))\)都应该在理论上非常接近0.5。
这时候,我们再回到我们的损失函数,再次看到这个函数,你可能还是认为“这个log函数太抽象了!怎么会判真的概率越大,损失越大呢!不行,我觉得还是应该判真的概率越大,损失越小才对!”那没关系,我们在log函数的前面加个负号,那这整个函数图像就上下颠倒了,就变为了在定义域\([0,1]\)中没有最大值,只有最小值,且最小值为0的单调递减函数了。同样的,我们需要给损失函数\(V\)加上个负号,再把我们以上所有结论全部都取反一遍。这时候,吴恩达老师课程中所述的生成器想要“最大化”损失,判别器想要“最小化”损失也就能解释了。