【XR-1】分块

题目描述

有一个长度为 \(n\) 的序列，xht37 现在想分块维护它。

PinkRabbit 要求他只准将序列分成 \(PR\) 种长度的块。

NaCly_Fish 要求他只准将序列分成 \(NF\) 种长度的块。

同一个人可能会要求 xht37 多次相同的块长。

xht37 想同时满足 PinkRabbit 和 NaCly_Fish 要求，只好使用两个人都允许的长度分块。

xht37 想知道，有多少种不同的分块方案，答案对 \(10 ^ 9 + 7\) 取模。

输入格式

第一行一个正整数 \(n\)，表示序列的长度。

第二行一个正整数 \(PR\)，表示 PinkRabbit 要求的分块长度的种类数。

第三行 \(PR\) 个正整数，表示 PinkRabbit 要求的 \(PR\) 种分块长度。

第四行一个正整数 \(NF\)，表示 NaCly_Fish 要求的分块长度的种类数。

第五行 \(NF\) 个正整数，表示 NaCly_Fish 要求的 \(NF\) 种分块长度。

输出格式

输出一行一个整数，表示不同分块方案的种类数对 \(10 ^ 9 + 7\) 取模的值。

解法探究

用桶可以得到两个人都要求的块长值，设其为\(L_k\)，由计数DP原理可以列出DP式：

\[dp_i = \Sigma_j \ dp_{i - L_j} \]

由于\(n \leq 10^{18}\)，我们考虑用矩阵快速幂加速这个式子，通常在矩阵快速幂时，都首先考虑每一位的单位乘积矩阵，即乘一次代表向前一位，即由\(dp_i\)推到\(dp_{i + 1}\)
考虑原矩阵是一个1*100的矩阵,最前面的a[1]代表dp[now],a[2] = dp[now - 1],a[3] = dp[now - 2]....
这是由于我们进行dp时需要前面最多100位的信息
对于第一列，即\(dp_{i + 1}\)的值，我们在转移矩阵相应的块长处设为1，即取上一个矩阵中的第\(L_i\)项，即\(dp[i + 1 - L_i]\)
对于第2_{100列，原封不动地取原来矩阵的第1}99项，所以在Matrix[i][i + 1] = 1(i \(\in [1,99]\))即可

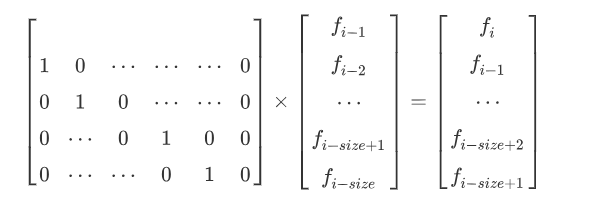
(截自洛谷题解区，所以是竖着的)

通过本题，应再次加深矩阵快速幂优化的印象，结合lxw巨的题目分书 luogu U281338进行理解，搞懂“乘一次前进一步”的过程

Code

#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7,N = 105,M = 100;
typedef long long ll;
int st[N],a[N],pr,nf,tp = 0,maxL = 0,res[N];
ll n;
struct Matrix{
	int p[N][N];
};
Matrix operator *(Matrix x,Matrix y)
{
	Matrix z;
	memset(z.p,0,sizeof(z.p));
	for(int i = 1;i <= M;i++)
		for(int j = 1;j <= M;j++)
			for(int k = 1;k <= M;k++)
				z.p[i][j] = (z.p[i][j] + 1ll * x.p[i][k] * y.p[k][j] % MOD) % MOD;
	return z;
}
inline Matrix ksm(Matrix base,ll pts)
{
	Matrix ret = base;
	pts--;
	for(;pts > 0;pts >>= 1,base = base * base)
		if(pts & 1)
			ret = ret * base;
	return ret;
}
int main()
{
	cin>>n;
	int x;
	cin>>pr;
	for(int i = 1;i <= pr;i++)
	{
		cin>>x;
		st[x] = 1;
	}
	cin>>nf;
	for(int i = 1;i <= nf;i++)
	{
		cin>>x;
		if(st[x] == 1)
			a[++tp] = x;
	}
	Matrix mul;
	memset(mul.p,0,sizeof(mul.p));
	for(int i = 1;i <= tp;i++) mul.p[a[i]][1] = 1;
	for(int i = 1;i <= M;i++) mul.p[i][i + 1] = 1;
	memset(st,0,sizeof(st));
	st[1] = 1;
	mul = ksm(mul,n);
	for(int i = 1;i <= 1;i++)
		for(int j = 1;j <= M;j++)
			for(int k = 1;k <= M;k++)
				res[j] += 1ll * st[k] * mul.p[k][j] % MOD,res[j] %= MOD;
	cout<<res[1];
	return 0;
 }