526互联

题解 BZOJ4399 魔法少女LJJ

发布时间 2023-06-09 16:32:26作者: Chronologika

前言

XXX：你瞅你长得那个B样，俺老孙就(氧化钙)......
这魔法(J8)少女能不能去死啊啊啊啊啊啊啊啊啊啊......

正文

"LJJ你是来搞笑的吧"

你说得对, 但是这数据就是骗人的.
首先看题面:

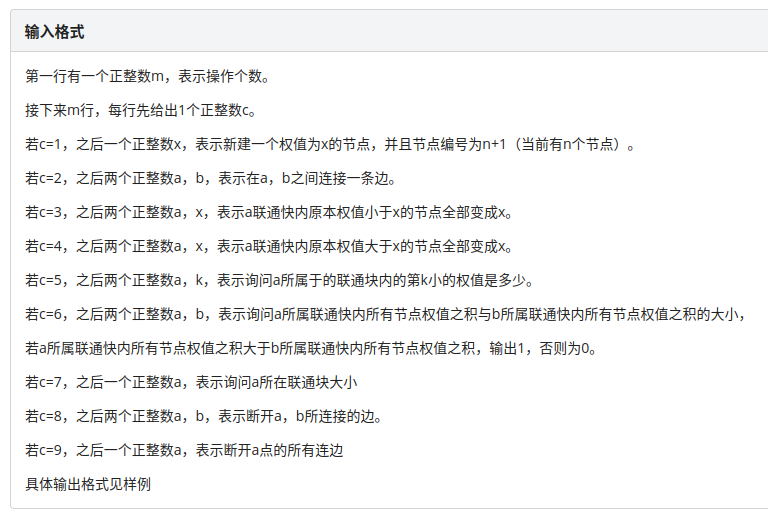
image

然后看样例:

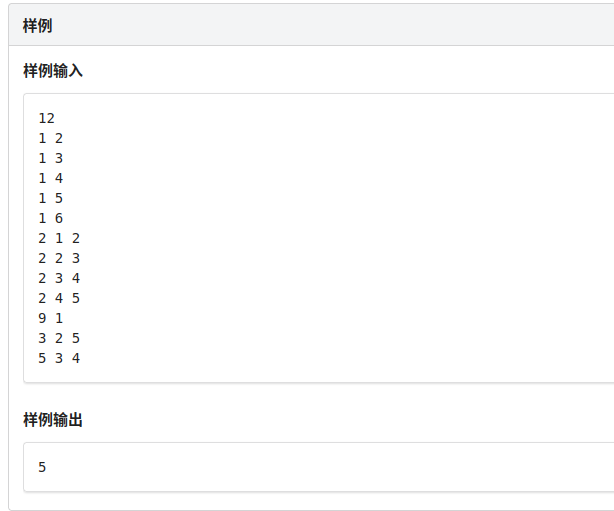
image

最后看数据范围:

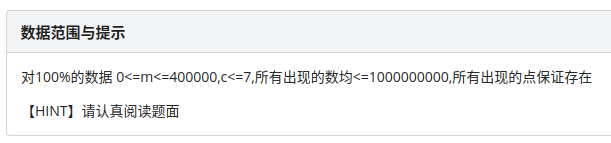
image

我惊奇的发现 \(c \le 7\) ! 家人们我真难绷qaq...

问题分析

显然第 \(8\) 条和第 \(9\) 条可以忽略, 直接看前 \(7\) 条即可.

  1. 线段树动态开点. 过于简单, 不予赘述.
  2. 线段树合并. 过于简单, 不予赘述.
  3. 很暴力地想, 因为维护的是一颗权值线段树(内部的值是单调的), 所以很容易将权值比 \(x\) 小的划分到一边(比 \(x\) 大的不用管), 先把它们删去, 记录删去了多少个点, 重新更改时把这些之前删去的值加上即可. 当然也不是不可以直接更改, 稍微在插点的时候判断一下就行.
  4. 原理同 \(3\) , 不予赘述.
  5. 查第 \(k\) 小值. 过于简单, 不予赘述.
  6. 比较两个连通块(两棵线段树)的点的乘积大小. 显然单纯求乘积一定会爆, 因为 \(\log_x(a \times b) = \log_x(a) + \log_x(b)\) , 所以我们可以通过求每一项的 \(\log_x\) 值的和来代替求每一项的积. 根据函数图像 \(f(x) = \log_a(x)\) 可知这样可以优化不少值域. 库函数提供了 \(\log 2\), \(\ln\) (即 \(\log\) ) 和 \(\log 10\). 这里不建议用 \(\log 10\), 因为它求出来的值太小, 会出现精度问题.
  7. 查连通块内点的个数. 过于简单, 不予赘述.

代码实现

想出这些远远不够, 还要在调代码上下一番功夫. 要注意的点都在下方的代码里:

#include <bits/stdc++.h>
using namespace std;

const int maxn(400005); 

inline int read() {
    int f(1), x(0);
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
    for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + (c & 15);
    return f * x;
}

int m, n, op[maxn], c1[maxn], c2[maxn], val[maxn];

// 离散化
int lb(int x) { return lower_bound(val + 1, val + 1 + n, x) - val; }

// 并查集优化
int fa[maxn], tot;
int getfa(int x) { return fa[x] == x ? x : fa[x] = getfa(fa[x]); }

int cnt, rt[maxn];
struct SegmentTree {
    int l, r, data;
    int lazy;
    long double mul;
};
array<SegmentTree, maxn << 5> t;

void pushup(int p) {
    t[p].data = t[t[p].l].data + t[t[p].r].data;
    t[p].mul = t[t[p].l].mul + t[t[p].r].mul;
}

void pushdown(int p) {
    if (t[p].lazy) {
        t[t[p].l].lazy = t[t[p].r].lazy = 1;
        t[t[p].l].data = t[t[p].l].mul = 0;
        t[t[p].r].data = t[t[p].r].mul = 0;
        t[p].lazy = 0;
    }
}

void insert(int& p, int l, int r, int c, double x, int y) {
    if (!p) p = ++cnt;
    if (l == r) {
        t[p].data += c;
        t[p].mul += x; // 就是这里不用再乘 c
        return;
    }

    pushdown(p);
    int mid = (l + r) >> 1;
    if (y <= mid) insert(t[p].l, l, mid, c, x, y);
    else insert(t[p].r, mid + 1, r, c, x, y);
    pushup(p);
}

void merge(int& a, int b, int l, int r) {
    if (!a || !b) {
        a = a ? a : b;
        return;
    }
    if (l == r) {
        t[a].data += t[b].data;
        t[a].mul += t[b].mul;
        return;
    }

    pushdown(a); pushdown(b);
    int mid = (l + r) >> 1;
    merge(t[a].l, t[b].l, l, mid);
    merge(t[a].r, t[b].r, mid + 1, r);
    pushup(a);
}

int ask_kth(int p, int l, int r, int k) {
    if (l == r) return val[l];
    pushdown(p);
    int mid = (l + r) >> 1;
    if (t[t[p].l].data >= k) return ask_kth(t[p].l, l, mid, k);
    else return ask_kth(t[p].r, mid + 1, r, k - t[t[p].l].data);
}

void del(int p, int l, int r, int x, int y) {
    if (!p || y < x) return;
    if (x <= l && r <= y) {
        t[p].data = t[p].mul = 0;
        t[p].lazy = 1;
        return;
    }

    int mid = (l + r) >> 1;
    pushdown(p);
    if (x <= mid) del(t[p].l, l, mid, x, y);
    if (y > mid) del(t[p].r, mid + 1, r, x, y);
    pushup(p);
}

int ask_num(int p, int l, int r, int x, int y) {
    if (!p || y < x) return 0;
    if (x <= l && r <= y) return t[p].data;
    pushdown(p);
    int mid = (l + r) >> 1, tmp(0);
    if (x <= mid) tmp += ask_num(t[p].l, l, mid, x, y);
    if (y > mid) tmp += ask_num(t[p].r, mid + 1, r, x, y);
    return tmp;
}

int main() {
    m = read();

    for (int i = 1; i <= m; ++i) {
        op[i] = read(); c1[i] = read();

        if (op[i] != 1 && op[i] != 7) c2[i] = read();
        if (op[i] == 1) val[++n] = c1[i];
        if (op[i] == 3 || op[i] == 4) val[++n] = c2[i];
    }
    // c1[] 和 c2[] 都是离散化前的权值

    // 离散化
    sort(val + 1, val + 1 + n);
    n = unique(val + 1, val + 1 + n) - (val + 1);
    // 离散化后的值域是 [1, n]
    // 最上面的 lb() 求出来的是离散化后的权值
    // log() 里面一定是离散化之前的权值, 否则求出来的成绩大小关系会改变

    for (int i = 1; i <= m; ++i) {
        if (op[i] == 1) {
            // 此时只有的 c1[] 是离散化前的点权值
            insert(rt[++tot], 1, n, 1, log(c1[i]), lb(c1[i]));
            fa[tot] = tot;
        }

        if (op[i] == 2) {
            int a = getfa(c1[i]), b = getfa(c2[i]);
            if (a != b) {
                fa[b] = a;
                merge(rt[a], rt[b], 1, n);
                // 并查集合并与线段树合并的方向要一致
            }
        }

        if (op[i] == 3) {
            int a = getfa(c1[i]), b = lb(c2[i]); // b 是离散化后的权值
            if (b == 1) continue;
            int num = ask_num(rt[a], 1, n, 1, b - 1); // num 表示要删去的有多少个点
            del(rt[a], 1, n, 1, b - 1);
            insert(rt[a], 1, n, num, num * log(c2[i]), b);
            // b 在函数对应的 y 的位置, 因为 y 要和 mid 比较, mid 又是通过离散化后的值域求出来的, 所以 y 的位置传的是离散化以后的权值 b
            // 这里面的 log() 已经乘上了 num , 因为删了 num 个点, 所以要加上 num 个 log() , 所以函数里面就不用乘 c
        }

        if (op[i] == 4) {
            int a = getfa(c1[i]), b = lb(c2[i]);
            if (b == n) continue;
            int num = ask_num(rt[a], 1, n, b + 1, n);
            del(rt[a], 1, n, b + 1, n);
            insert(rt[a], 1, n, num, num * log(c2[i]), b);
        }

        if (op[i] == 5) {
            int a = getfa(c1[i]);
            printf("%d\n", ask_kth(rt[a], 1, n, min(c2[i], t[rt[a]].data)));
        }

        if (op[i] == 6) {
            int a = getfa(c1[i]), b = getfa(c2[i]);
            printf("%d\n", t[rt[a]].mul > t[rt[b]].mul);
        }

        if (op[i] == 7) {
            int a = getfa(c1[i]);
            printf("%d\n", t[rt[a]].data); // 直接输出就行
        }
    }
}

结语

敲这B代码跟深井冰似的... 不过以后应该再也不会害怕调恶心的代码了吧...