一.
OSU!
题目背景
原 《产品排序》 参见P2577
题目描述
osu 是一款群众喜闻乐见的休闲软件。
我们可以把 osu 的规则简化与改编成以下的样子:
一共有 \(n\) 次操作,每次操作只有成功与失败之分,成功对应 \(1\),失败对应 \(0\),\(n\) 次操作对应为 \(1\) 个长度为 \(n\) 的 01 串。在这个串中连续的 \(X\) 个 \(1\) 可以贡献 \(X^3\) 的分数,这 \(x\) 个 \(1\) 不能被其他连续的 \(1\) 所包含(也就是极长的一串 \(1\),具体见样例解释)
现在给出 \(n\),以及每个操作的成功率,请你输出期望分数,输出四舍五入后保留 \(1\) 位小数。
输入格式
第一行有一个正整数 \(n\),表示操作个数。接下去 \(n\) 行每行有一个 \([0,1]\) 之间的实数,表示每个操作的成功率。
输出格式
只有一个实数,表示答案。答案四舍五入后保留 \(1\) 位小数。
样例 #1
样例输入 #1
3
0.5
0.5
0.5
样例输出 #1
6.0
提示
【样例说明】
\(000\) 分数为 \(0\),\(001\) 分数为 \(1\),\(010\) 分数为 \(1\),\(100\) 分数为 \(1\),\(101\) 分数为 \(2\),\(110\) 分数为 \(8\),\(011\) 分数为 \(8\),\(111\) 分数为 \(27\),总和为 \(48\),期望为 \(\dfrac{48}8 = 6.0\)。
\(n \leq 1 \times 10 ^ 5\)。
一.背景
《osu!》是一款Microsoft Windows平台上的同人音乐游戏。由Dean Herbert(Peppy)使用.NET Framework中的C#编写,后来升级为.NET 6.0并陆续在Mac OS、iOS、Android、Windows Phone等平台推出。游玩方式的设计参考了《押忍!战斗!应援团》、《太鼓达人》、《BeatmaniaIIDX》、《O2Jam》和《DJMax》,游戏共有osu!标准模式、osu!taiko、osu!catch以及osu!mania共四种玩法,深受各类音乐游戏玩家的喜爱。
二.前言
先用状压的思想做但是发现\(n\leq 1\times10^5\)
对于每个状态算出它的概率和求和然后加到一块容易写出一下代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
inline int read(){
int f(1),x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f*x;
}
inline void Write(int x){
if(x>9) Write(x/10);
putchar(x%10+'0');
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
Write(x);
putchar('\n');
}
}
using namespace Testify;
const int N=1e5+5;
int n;
double op[N];
inline double P(int s){
double Ecstasy(1);
int cnt(0);
for(register int i=1;i<=n;i++){
cnt++;
if(s&1){
Ecstasy*=op[cnt];
}
else{
Ecstasy*=(1.0-op[cnt]);
}
if(s){
s>>=1;
}
}
return Ecstasy;
}
inline double Sigma(int s){
int Ecstasy(0);
int cnt=0;
while(s){
while(s&1){
cnt++;
s>>=1;
}
Ecstasy+=(cnt*cnt*cnt);
cnt=0;
s>>=1;
}
return Ecstasy;
}
signed main(){
n=read();
for(register int i=1;i<=n;i++){
scanf("%lf",&op[i]);
}
double Tempestissimo(0);
for(register int s=1;s<(1<<n);s++){
double gai=P(s);
Tempestissimo+=(gai*Sigma(s));
}
printf("%.1lf",Tempestissimo);
return 0;
}
然后得了10分
因为\(n\)数据太大,肯定不能暴力枚举
三.思路
对于每个排列
$\ \ \ \ \ \ \ (x+1)^3 $
\(=(x+1)\times (x+1)\times (x+1)\)
\(=(x^2+2x+1)\times (x+1)\)
\(=x^3+x^2+2x^2+2x+x+1\)
\(=x^3+3x^2+3x+1\)
所以
\((x+1)^3\)比\(x^3\)多了\(3x^2+3x+1\)
即\(x^3[i]=x^3[i-1]+3\times x^2[i-1]+3\times x^1[i-1]+1\)
$\ \ \ \ \ \ \ (x+1)^2 $
\(=(x+1)\times (x+1)\)
\(=x^2+2\times x+1\)
所以
\((x+1)^2\)比\(x^2\)多了\(2\times x+1\)
即\(x^2[i]=x^2[i-1]+2\times x^1[i-1]+1\)
那么我们只需要维护\(x^2\)和\(x^1\)的期望 就能求出\((x+1)^3\)力


设\(dp[i]\)表示前\(i\)种情况の期望,即\(x^3[i]\)
\(x1[i]\)表示第\(i\)种情况的\(x\)の期望,即\(x^2[i]\)
\(x2[i]\)表示第\(i\)种情况的\(x^2\)の期望,即\(x^1[i]\)
那么我们可以得到式子
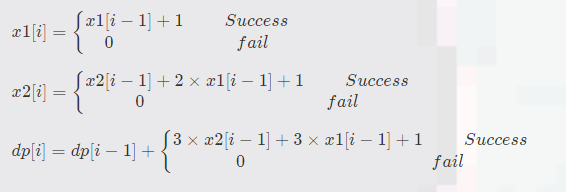
所以只要在算出上式再$\times $上本次操作の概率就能得出期望力????
不难得到\(AC\)代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n;
double dp[N],x1[N],x2[N],op[N];
signed main(){
scanf("%lld",&n);
for(register int i=1;i<=n;i++){
scanf("%lf",&op[i]);//概率
}
// x1[0]=x2[0]=dp[0]=0;//初始化
for(register int i=1;i<=n;i++){
x1[i]=op[i]*(x1[i-1]+1);
x2[i]=op[i]*(x2[i-1]+2*x1[i-1]+1);
dp[i]=dp[i-1]+op[i]*(3*x2[i-1]+3*x1[i-1]+1);
}
printf("%.1lf",dp[n]);
return 0;
}
完结撒花????
二.列队春游
题目

前言
出生镇楼
思路:
- 打个暴力先
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
inline int read(){
int f(1),x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f*x;
}
inline void Write(int x){
if(x>9) Write(x/10);
putchar(x%10+48);
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
Write(x);
putchar('\n');
}
}
using namespace Testify;
const int N=305;
int n,tot(0);
int a[N];
double Tempestissimo(0);
signed main(void){
n=read();
a[0]=114514;
for(register int i=1;i<=n;i++){
a[i]=read();
}
sort(a+1,a+n+1);
do{
tot++;
Tempestissimo++;
for(register int i=2;i<=n;i++){
int cnt=0;
for(register int j=i-1;j>=0;j--){
cnt++;
if(a[j]>=a[i]){
break;
}
}
Tempestissimo+=cnt;
}
}while(next_permutation(a+1,a+n+1));
printf("%.2lf",Tempestissimo/tot);
return 0;
}
对于每种情况都模拟一遍最后加上然后除以总数\(tot\)即为答案
- 组合数学
对于每个小朋友都算出对应情况的方案数然后乘起来每个小朋友每种视野的期望就能得到答案
①预处理出对于每个小朋友 有多少身高比他矮的 小朋友 (注意一点身高和小朋友一样高的算比他高的,否则只能得50分) 假设\(h[i]\)表示对于第\(i\)个小朋友有多少身高比他矮的 小朋友
② 循坏枚举小朋友\(i\)和比小朋友身高低的忍术\(j\)
③ 对于每种比他矮的小朋友 (\(j+1\)即视野期望) 通过逆天 组合数学 得到答案
④ 组合数学从两方面考虑,一是第\(i\)个的小朋友前\(j+1\)个人 (即前面矮的j个人的前一个) 是身高比i大的小朋友
那么身高较矮的\(j\)个小朋友方案数为\(A_{h[i]}^j\)
从身高高或相等的小朋友抽取一个小朋友 方案数为\(A_{n-h[i]-1}^1\)
剩下的人随便放都可以,方案数\(A_{n-j-2}^{n-j-2}\)
将剩下\(n-j-2\)个人看做一个整体,将已经确定的\(j+2\)个人看做一个整体,那么就有\(n-j-1\)个空位插入\(1\)个整体,方案数为\((n-j-1)\)
⑤ 第二方面是第\(i\)个的小朋友前\(j+1\)个人 (即前面矮的j个人的前一个) 是老师
那么这种情况下 那么身高较 矮的\(j\)个小朋友方案数为\(A_{h[i]}^j\)
剩下的\(n-j-1\)个都是随便排,有方案数\(A_{n-j-1}^{n-j-1}\)种,
和上面不同的地方是,\(j+1\)个小朋友看做一个整体,这个整体一定在老师后面,即队伍最前面,就不能插空了
总结:设\(Tempestissimo\)为 总 的方案数,则
接下来在每次循环中都将 单独的 方案数乘上视野期望(即j+1)在累计到\(ans\)中即可!!!!!!
完结撒花!!不放代码捏
思路借鉴@Trump_ 


三.矩阵粉刷
题目描述
为了庆祝新的一年到来,小M决定要粉刷一个大木板。大木板实际上是一个\(W*H\)的方阵。小M得到了一个神奇的工具,这个工具只需要指定方阵中两个格子,就可以把这两格子为对角的,平行于木板边界的一个子矩形全部刷好。小M乐坏了,于是开始胡乱地使用这个工具。
假设小M每次选的两个格子都是完全随机的(方阵中每个格子被选中的概率是相等的),而且小M使用了\(K\)次工具,求木板上被小M粉刷过的格子个数的期望值是多少。
输入格式
第一行是整数\(K,W,H\)
输出格式
一行,为答案,四舍五入保留到整数。
样例
样例输入
1 3 3
样例输出
4
样例解释
准确答案约为3.57
数据范围与提示
\(100%\) 的数据满足:\(1 ≤ W, H ≤ 1000, 0 ≤ K ≤ 100\)
考虑对于位置\((i,j)\)不被粉刷的可能性
显然,考虑粉刷其他地方的情况
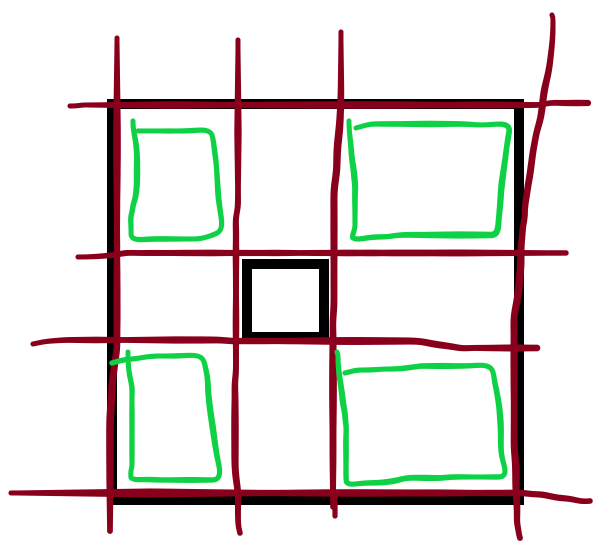
如图,找出每个红色的区域,设面积为\(S\),那么顶点可以取的地方显然为\(S^2\),注意不是\(C(S,2)\)
减去重复的绿色区域,就可以求出了,还是比较简单的
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
inline int read(){
int f(1),x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f*x;
}
inline void Write(int x){
if(x>9) Write(x/10);
putchar(x%10+'0');
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
Write(x);
putchar('\n');
}
}
using namespace Testify;
//???????????
int n,m,k;
inline double qpow(double x,int k){//x^k
double op=1;
while(k){
if(k&1) op=op*x;
x=x*x;
k>>=1;
}
return op;
}
inline double C(int x){
if(x==1) return 1;
return x*x;
}
double Tempestissimo(0);
signed main(){
k=read(),n=read(),m=read();
for(register int i=1;i<=n;i++){
for(register int j=1;j<=m;j++){
double s1=(i-1)*(m);
double s2=(n-i)*(m);
double s3=(j-1)*(n);
double s4=(m-j)*(n);
double d1=(i-1)*(j-1);
double d2=(n-i)*(j-1);
double d3=(m-j)*(n-i);
double d4=(m-j)*(i-1);
double qwq=(C(s1)+C(s2)+C(s3)+C(s4)-C(d1)-C(d2)-C(d3)-C(d4));
double qaq=(C(n*m));
Tempestissimo+=(1-qpow(qwq/qaq,k));
}
}
// cout<<Tempestissimo;
write(Tempestissimo+0.5);
return 0;
}
四.守卫者的挑战
题目描述
打开了黑魔法师Vani的大门,队员们在迷宫般的路上漫无目的地搜寻着关押applepi的监狱的所在地。突然,眼前一道亮光闪过。“我,Nizem,是黑魔法圣殿的守卫者。如果你能通过我的挑战,那么你可以带走黑魔法圣殿的地图……”瞬间,队员们被传送到了一个擂台上,最初身边有一个容量为K的包包。
擂台赛一共有N项挑战,各项挑战依次进行。第i项挑战有一个属性ai,如果ai>=0,表示这次挑战成功后可以再获得一个容量为ai的包包;如果ai=-1,则表示这次挑战成功后可以得到一个大小为1 的地图残片。地图残片必须装在包包里才能带出擂台,包包没有必要全部装满,但是队员们必须把 【获得的所有的】地图残片都带走(没有得到的不用考虑,只需要完成所有N项挑战后背包容量足够容纳地图残片即可),才能拼出完整的地图。并且他们至少要挑战成功L次才能离开擂台。
队员们一筹莫展之时,善良的守卫者Nizem帮忙预估出了每项挑战成功的概率,其中第i项挑战成功的概率为pi%。现在,请你帮忙预测一下,队员们能够带上他们获得的地图残片离开擂台的概率。
输入格式
第一行三个整数N,L,K。
第二行N个实数,第i个实数pi表示第i项挑战成功的百分比。
第三行N个整数,第i个整数ai表示第i项挑战的属性值.
输出格式
一个整数,表示所求概率,四舍五入保留6 位小数。
样例
样例输入1
3 1 0
10 20 30
-1 -1 2
样例输出1
0.300000
样例输入2
5 1 2
36 44 13 83 63
-1 2 -1 2 1
样例输出2
0.980387
数据范围与提示
若第三项挑战成功,如果前两场中某场胜利,队员们就有空间来容纳得到的地图残片,如果挑战失败,根本就没有获得地图残片,不用考虑是否能装下;
若第三项挑战失败,如果前两场有胜利,没有包来装地图残片,如果前两场都失败,不满足至少挑战成功次()的要求。因此所求概率就是第三场挑战获胜的概率。
对于 \(100%\) 的数据,保证\(0<=K<=2000,0<=N<=200,-1<=ai<=1000,0<=L<=N,0<=pi<=100。\)
考虑背包dp
设\(dp[i][j][k]\),为已经打了\(i\)场比赛,赢了\(j\)场,剩下的背包容量为\(k\)时的概率
\(level[i].p\)为概率,\(level[i].shengyiwu\)是背包容量加减情况
先把\(level\)按分配背包多少排序,这样可以先把背包都拿上,再去获得地图残片?
当下一场比赛可能获得地图残片时,即背包容量\(-1\),分两种情况,一是下一场比赛获胜,转移方程即为
如果下一次比赛输
当下一场比赛能获得背包时,即背包容量\(-1\),分两种情况,一是下一场比赛获胜,转移方程即为
如果下一次比赛输
所以就能得到答案力
这里注意背包容量最多考虑到\(n\)就行了,为什么呢?
因为即使每场比赛都打赢,才会获得\(n\)个地图残片,这时剩下背包容量为0就行了,背包里最多才能放\(n\)个东西,如果你背包容量\(>n\)了,可能不太好统计,因为你不确定背包最大为多少?
所以上面的转移方程可以优化为
最后统计起来打完\(n\)场比赛,已经打赢了\(≥l\)场比赛的,剩下背包数量\(0~n\)的期望(概率)就行
有人可能会说:你\(min(k+level[i].shengyiwu,n)\)难道不会让背包容量为\(n\)的情况多算吗?
当然会多算,但是这样可以把比\(n\)还大的情况都累计到\(n\)上就行,所以最后统计可以完全
点击抄袭代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace Testify{
inline int read(){
int f(1),x(0);
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
return f*x;
}
inline void Write(int x){
if(x>9) Write(x/10);
putchar(x%10+48);
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
Write(x);
putchar('\n');
}
}
using namespace Testify;
const int N=1e5+5;
int n,l,K;
double tmp;
struct node{
int shengyiwu;
double p;
friend inline bool operator <(const node &a,const node &b){
return a.shengyiwu>b.shengyiwu;
}
}level[N];
double dp[205][205][505];//打了i场比赛,已经赢了j场,剩下背包の容量为k的概率
signed main(void){
n=read(),l=read(),K=read();
for(register int i=1;i<=n;i++){
scanf("%lf",&tmp);
level[i].p=tmp/100;
}
for(register int i=1;i<=n;i++){
level[i].shengyiwu=read();
}
sort(level+1,level+n+1);
dp[0][0][min(K,n)]=1;
for(register int i=1;i<=n;i++){
for(register int j=0;j<=i;j++){
for(register int k=0;k<=n;k++){
if(level[i].shengyiwu==-1){//背包-1
if(j-1>=0&&k-1>=0){//赢
dp[i][j][k-1]+=dp[i-1][j-1][k]*level[i].p;
}
dp[i][j][k]+=dp[i-1][j][k]*(1-level[i].p);
}
else {//获得背包
if(j-1>=0){//赢
dp[i][j][min(k+level[i].shengyiwu,n)]+=dp[i-1][j-1][k]*level[i].p;
}
dp[i][j][k]+=dp[i-1][j][k]*(1-level[i].p);
}
}
}
}
double Tempestissimo(0);
for(register int i=l;i<=n;i++){
for(register int j=0;j<=n;j++){
Tempestissimo+=dp[n][i][j];
}
}
printf("%.6lf",Tempestissimo);
return 0;
}
五.概率充电器
[SHOI2014] 概率充电器
题目描述
著名的电子产品品牌 SHOI 刚刚发布了引领世界潮流的下一代电子产品——概率充电器:
“采用全新纳米级加工技术,实现元件与导线能否通电完全由真随机数决定!SHOI 概率充电器,您生活不可或缺的必需品!能充上电吗?现在就试试看吧!”
SHOI 概率充电器由 \(n-1\) 条导线连通了 \(n\) 个充电元件。进行充电时,每条导线是否可以导电以概率决定,每一个充电元件自身是否直接进行充电也由概率决定。随后电能可以从直接充电的元件经过通电的导线使得其他充电元件进行间接充电。
作为 SHOI 公司的忠实客户,你无法抑制自己购买 SHOI 产品的冲动。在排了一个星期的长队之后终于入手了最新型号的 SHOI 概率充电器。你迫不及待地将 SHOI 概率充电器插入电源——这时你突然想知道,进入充电状态的元件个数的期望是多少呢?
输入格式
第一行一个整数 \(n\)。概率充电器的充电元件个数。充电元件由 \(1 \sim n\) 编号。
之后的 \(n-1\) 行每行三个整数 \(a, b, p\),描述了一根导线连接了编号为 \(a\) 和 \(b\) 的充电元件,通电概率为 \(p\%\)。
第 \(n+2\) 行 \(n\) 个整数 \(q_i\)。表示 \(i\) 号元件直接充电的概率为 \(q_i\%\)。
输出格式
输出一行一个实数,为能进入充电状态的元件个数的期望,四舍五入到小数点后 6 位小数。
样例 #1
样例输入 #1
3
1 2 50
1 3 50
50 0 0
样例输出 #1
1.000000
样例 #2
样例输入 #2
5
1 2 90
1 3 80
1 4 70
1 5 60
100 10 20 30 40
样例输出 #2
4.300000
提示
对于 \(30\%\) 的数据,\(n \leq 5 \times 10^3\)。
对于 \(100\%\) 的数据,\(n \leq 5 \times 10^5\),\(0 \leq p,q_i \leq 100\)。
题太逆天了,一开始没考虑环打逆天暴力就得10分,现在还是100分\(Unaccept\)呜呜呜,未完待续...
