引入
树链剖分用于将树分割成若干条链的形式,以维护树上路径的信息。
具体来说,将整棵树剖分为若干条链,使它组合成线性结构,然后用其他的数据结构维护信息。
By OI-Wiki
大多数情况下,「树链剖分」都指「重链剖分」,本文就只讲一下「重链剖分」。
前置芝士(重链剖分中的一些定义 \(\&\) 性质)
对于树上的任意一个结点,
-
重儿子 表示其子结点中子树最大(子树中包含的结点个数最多)的子结点;若有多个子树最大的子结点,任取其一;若无子结点,则无重儿子。
(生动形象) -
轻儿子 表示其除重儿子外的所有子结点。
-
重边 表示从此结点到其重儿子的边。
-
轻边 表示从此结点到其轻儿子的边。
-
重链 表示由若干条首尾连接的重边构成的链(落单的节点也算作一条重链)。
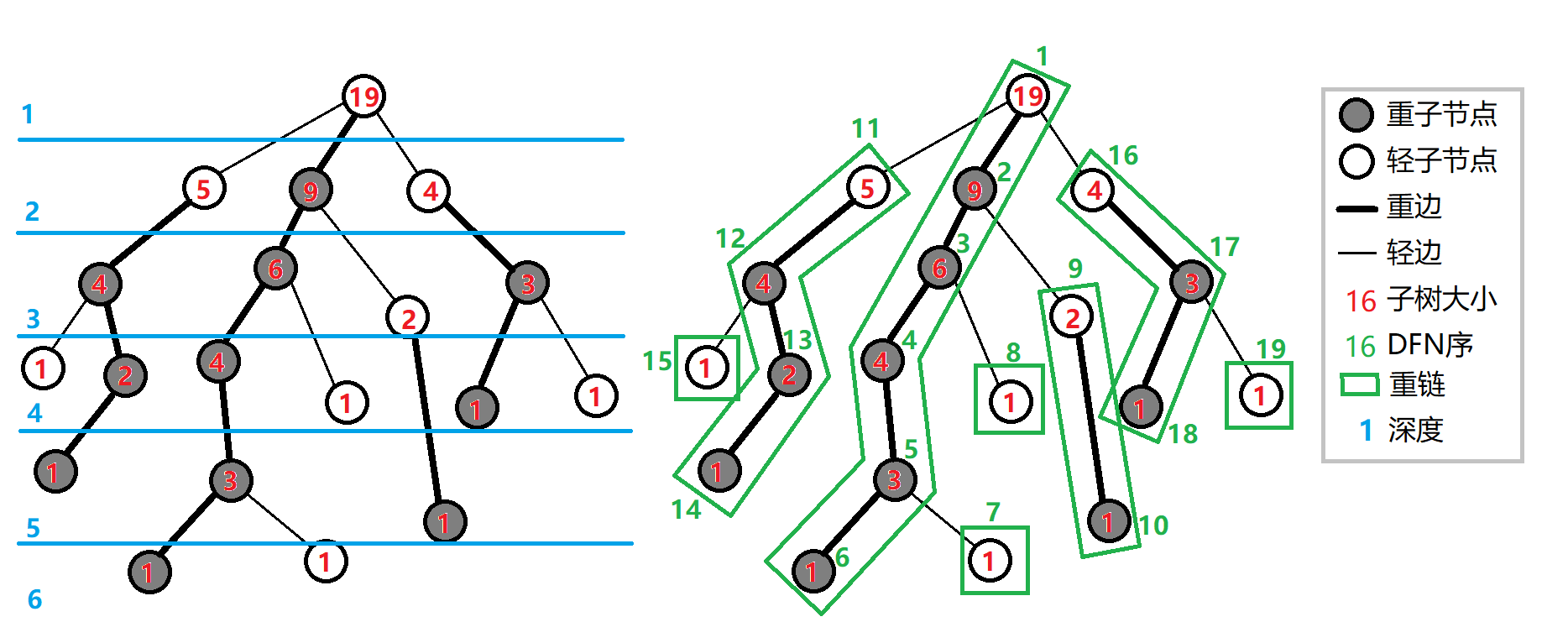
用一下 Wiki 上的图。
如图,可以发现,在以上定义过后,整棵树就可以被剖分成若干条重链。
而且有一些有趣的性质:
-
轻儿子必在一重链顶端。
-
树上的任意一条路径可以被划分成不超过 \({\cal O}(\log n)\) 条连续的链。
证明先咕着。
应用
树剖主要针对的是如下问题:
P3384 【模板】重链剖分/树链剖分
已知一棵包含 \(N\) 个结点的树(连通且无环),每个结点上包含一个数值,需要支持以下操作:
1 x y z,表示将树从 \(x\) 到 \(y\) 结点最短路径上所有结点的值都加上 \(z\)。
2 x y,表示求树从 \(x\) 到 \(y\) 结点最短路径上所有结点的值之和。
3 x z,表示将以 \(x\) 为根节点的子树内所有结点值都加上 \(z\)。
4 x表示求以 \(x\) 为根节点的子树内所有结点值之和。对于 \(100\%\) 的数据: \(1\le N \leq {10}^5\),\(1\le M \leq {10}^5\)。
是不是很像线段树之类的题?
没错,树剖就是这个思想,将树上的操作映射到一段连续的序列上,变成区间操作,再用线段树解决。
代码中的一些定义
- \({\bf root}\) 表示树的根节点。
对于树上的任意节点 \(u\),
- \({\bf fa}[u]\) 表示 \(u\) 的父亲编号。
- \({\bf dep}[u]\) 表示 \(u\) 在树中的深度。
- \({\bf sz}[u]\) 表示以 \(u\) 为根的子树中的结点个数。
- \({\bf son}[u]\) 表示 \(u\) 的重儿子。
- \({\bf top}[u]\) 表示 \(u\) 所在重链的顶点(深度最小的结点)。
- \({\bf id}[u]\) 表示 \(u\) 映射到新序列上的位置。
- \({\bf nw}[{\bf id}[u]]\) 表示 \(u\) 映射到新序列上后的点权(即 \({\bf nw}[i]\) 表示新序列第 \(i\) 个位置的权值,就是存下新的序列)。
对于本题,需要的代码如下:
const int N = 1e5 + 10, M = N << 1;
int n, m, root, mod;
int h[N], ne[M], e[M], w[M], idx;
int id[N], nw[N], cnt;
int dep[N], top[N], sz[N], fa[N], son[N];
树剖(重链剖分)代码实现
首先,常用两个 \(dfs\) 解决。
之后,就是线段树模板。
最后,根据题目需要实现一些将询问转化为新序列的区间操作的函数。
\(\large \text{Part 1}\)
第一个 \(dfs\) 标记所有重儿子,顺便处理深度、父亲等。
\(\large \color{gray} \cal{Code}\) (详解看注释)
void dfs1(int u, int father, int depth){
dep[u] = depth, fa[u] = father, sz[u] = 1;
// 维护当前节点的dep, fa, sz
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == father) continue;
// 跳过返祖的边
dfs1(j, u, depth + 1);
// 遍历以子结点为根的子树,记得传对参数
sz[u] += sz[j];
// 因为此子结点j以下的节点都遍历完了,可以直接更新当前节点u的sz
if(sz[son[u]] < sz[j]) son[u] = j;
// 如果当前儿子的sz大于了之前的重儿子,更新重儿子
}
}
// ...
dfs(root, -1, 1) // 主函数调用,注意从根节点开始
第二个 \(dfs\) 处理出重链,并将树上的点映射到新的序列中。
处理重链实际上就是标记每个结点 \(u\) 所在重链的顶点 \({\bf top}[u]\)(因为后面只会用到这个)。
映射的部分有些需要注意的地方(重点),具体看代码:
\(\large \color{gray} \cal{Code}\) (详解看注释)
// u是当前结点,t是当前结点所在重链的顶点
id[u] = ++cnt, nw[cnt] = w[u], top[u] = t;
// 在序列上新建一个结点,下标为cnt
// 将点权映射至新序列,标记top[u]
if(!son[u]) return;
// 如果是叶节点,即没有重儿子,跳过
dfs2(son[u], t);
// 这里要注意,为了保证重链在映射的新序列中是连续的,向下遍历时一定要优先遍历重儿子
// 重儿子必定不在重链的顶端,重儿子所在重链的顶端和其父节点是一样的
// 随后处理轻儿子
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == son[u] || j == fa[u]) continue;
// 重儿子前面遍历过了,跳过;返租边照样跳过
dfs2(j, j);
// 轻儿子肯定在一条重链的顶端
}
}
\(\large \text{Part 2}\)
线段树板子,只需基础的区间加,求区间和即可。
注意维护的是映射的新序列, \(\rm build\) 时要用新序列 \(\bf nw\),代码就不展示了,最后的整合代码里有。
还不会线段树看这篇博客 \(\large \Longrightarrow\) Link。
\(\large \text{Part 3}\)
实现此题的四种操作。
-
1 x y z,表示将树从 \(x\) 到 \(y\) 结点最短路径上所有结点的值都加上 \(z\)。
因为树上的任意一条路径可以被划分成不超过 \({\cal O}(\log n)\) 条连续的链,而每一条重链映射到新序列上都是一段连续的区间,于是就转化成了 \({\cal O}(\log n)\) 个区间操作,具体过程还是有许多的细节,见下:
\(\large \color{gray} \cal{Code}\) (详解看注释)
void update_path(int u, int v, int k){
// 表示将树从u到v的最短路径上所有结点的值都加上k
// 这里将u和v一直往上跳,每次跳到所在重链的顶端再上一个结点,直到跳到两个点的LCA位为止
while(top[u] != top[v]){ // 这里注意,两点跳到同一条重链上时就结束,后面单独分析
if(dep[top[u]] < dep[top[v]]) swap(u, v);
// 注意一定是要比较top[u]和top[v]的深度,否则有可能跳到LCA上面,画个图看看就知道了
update(1, id[top[u]], id[u], k);
// 每跳过一条重链,就区间修改一次
// 注意映射时深度越浅在越前面,左右别搞反了
u = fa[top[u]];
// 注意要跳到所在重链的顶点的父节点,不然一直在原地跳
}
// 最后在同一条重链上时单独处理
if(dep[u] < dep[v]) swap(u, v);
update(1, id[v], id[u], k);
// 还是注意顺序
}
-
3 x z,表示将以 \(x\) 为根节点的子树内所有结点值都加上 \(z\)。
这个其实很简单,因为映射新序列时是按照的搜索序,一个子树中所有结点必定是连续的。
代码很简单:
\(\large \color{gray} \cal{Code}\)
void update_tree(int u, int k){
update(1, id[u], id[u] + sz[u] - 1, k);
// 右边界 + sz[u] - 1 即可
}
另外两个查询的操作类似,这里也就不赘述了。
完整代码
最后是完整的巨长 \(\color{red}{\cal 210}\) 行 \(\color{gray}{\cal Code}\) :
可能是我的一些 Max/Min/read 模板太臃肿了。
不开 \(\rm long \ long\) 见祖宗哦
#include <map>
#include <queue>
#include <cmath>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
namespace oi{
template <class T>
inline T Abs(T x){return x > 0 ? x : -x;}
template <class T>
inline T Max(T a, T b){return a > b ? a : b;}
template <class T, class... TT>
inline T Max(T a, TT... b){
T res = Max(b...);
return Max(a, res);
}
template <class T>
inline T Min(T a, T b){return a < b ? a : b;}
template <class T, class... TT>
inline T Min(T a, TT... b){
T res = Min(b...);
return Min(a, res);
}
template <class T>
inline void read(T &x){
x = 0;
char ch = getchar();
bool flag = 0;
while(ch < '0' || ch > '9') flag |= ch == '-', ch = getchar();
while(ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
flag ? x = -x : 0;
}
template <class T, class... TT>
inline void read(T &x, TT &...xx){
read(x), read(xx...);
}
}
using namespace std;
using namespace oi;
typedef long long ll;
typedef unsigned long long ull;
const int N = 1e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
int n, m, root, mod;
int h[N], ne[M], e[M], w[M], idx;
int id[N], nw[N], cnt;
int dep[N], top[N], sz[N], fa[N], son[N];
struct Segment_Tree{
int l, r;
ll add, sum;
}tr[N << 2];
void init(){
memset(h, -1, sizeof h);
}
inline void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs1(int u, int father, int depth){
dep[u] = depth, fa[u] = father, sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == father) continue;
dfs1(j, u, depth + 1);
sz[u] += sz[j];
if(sz[son[u]] < sz[j]) son[u] = j;
}
}
void dfs2(int u, int t){
id[u] = ++cnt, nw[cnt] = w[u], top[u] = t;
if(!son[u]) return;
dfs2(son[u], t);
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == son[u] || j == fa[u]) continue;
dfs2(j, j);
}
}
inline void pushup(int u){
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
inline void pushdown(int u){
if(tr[u].add){
Segment_Tree &root = tr[u], &le = tr[u << 1], &ri = tr[u << 1 | 1];
le.add += root.add;
ri.add += root.add;
le.sum += root.add * (le.r - le.l + 1);
ri.sum += root.add * (ri.r - ri.l + 1);
root.add = 0;
}
}
void build(int u, int l, int r){
tr[u] = {l, r, 0, nw[l]};
if(l == r) return;
int mid = (l + r) >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
void update(int u, int l, int r, int c){
if(l <= tr[u].l && tr[u].r <= r){
tr[u].add += c;
tr[u].sum += c * (tr[u].r - tr[u].l + 1);
return;
}
pushdown(u);
int mid = (tr[u].l + tr[u].r) >> 1;
if(l <= mid) update(u << 1, l, r, c);
if(r > mid) update(u << 1 | 1, l, r, c);
pushup(u);
}
ll query(int u, int l, int r){
if(l <= tr[u].l && tr[u].r <= r){
return tr[u].sum;
}
pushdown(u);
int mid = (tr[u].l + tr[u].r) >> 1;
ll res = 0;
if(l <= mid) res += query(u << 1, l, r);
if(r > mid) res += query(u << 1 | 1, l, r);
return res;
}
void update_path(int u, int v, int k){
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]]) swap(u, v);
update(1, id[top[u]], id[u], k);
u = fa[top[u]];
}
if(dep[u] < dep[v]) swap(u, v);
update(1, id[v], id[u], k);
}
void update_tree(int u, int k){
update(1, id[u], id[u] + sz[u] - 1, k);
}
ll query_path(int u, int v){
ll res = 0;
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]]) swap(u, v);
res += query(1, id[top[u]], id[u]);
u = fa[top[u]];
}
if(dep[u] < dep[v]) swap(u, v);
res += query(1, id[v], id[u]);
return res;
}
ll query_tree(int u){
return query(1, id[u], id[u] + sz[u] - 1);
}
int main(){
init();
read(n, m, root, mod);
for(int i = 1; i <= n; ++i) read(w[i]);
int a, b;
for(int i = 1; i < n; ++i){
read(a, b);
add(a, b), add(b, a);
}
dfs1(root, -1, 1);
dfs2(root, root);
build(1, 1, n);
int op, u, v, k;
while(m--){
read(op, u);
if(op == 1){
read(v, k);
update_path(u, v, k);
}
else if(op == 3){
read(k);
update_tree(u, k);
}
else if(op == 2){
read(v);
printf("%lld\n", query_path(u, v) % mod);
}
else printf("%lld\n", query_tree(u) % mod);
}
return 0;
}
进阶
/#TODO#/