0 比赛经过
比赛还没开始的时候就感觉状态不太好。果然。
总归到底都是一个心态问题。
A 题经过
看 A 题,结果半天看不懂,一开始没有注意到一定要在黑格子上操作。扔到 DeepL 上翻译了一下,再手玩一下样例就做出来了,速度有点慢。CF 怎么这么喜欢出分讨题啊。
看题目不能太急,要一个一个单词的看。
B 题经过
B 题题面有点绕。看懂题之后其实想偏了一会,被样例图片误导了一会,直到开始动手玩样例的时候才发现其实不难。马上写出来了。玩样例是好的。
C 题经过
一看到有关两个质数之和的乱搞题就要想到 \(2\)。我就是这样的,然后顺藤摸瓜马上想到了正解。但是我还是想复杂了,因为我当时比较急,认为奇质数要轮换着填,如果填完了奇质数还有空要填就直接不填了,不可能还有方案。然后就 Wrong Answer On Test \(4\) 了。
考试的时候心态要放平稳,不能急,要多想一会,如果心态不好就及时调整。
D & E 题经过
说是 D & E,实际上 E 基本没看。
一看到 D,发现是一道 \(\gcd\) 的题。然而这种题我最不会了。所以刚开始有点怕,结果没注意到 \(a_i \leq 10^6\) 的数据范围。基本把做 D 的三个性质都想到了,然后就随便糊了一个认为很对的 \(\mathcal{O}(168n)\) 的乱搞解,结果贼难写,然后还 T 了。放平心态后又重新看了一遍题,还是没看到 \(a_i \leq 10^6\) 的数据范围。
中途有想过要不要跳 E,但是后来放弃了这个想法。其实我曾经做过与 E 极其类似的一道 dp 题。
所以,数据范围有可能是题目的一个突破口。而且在一道题毫无进展的时候可以换一道题,换换脑子。
但是确实,E 和 F 确实比较超出我本身的真实水平。所以多练也是必须的。
A. Not Shading
0 鲜花
我需要提升一眼盯真的能力。
1 题目大意
1.1 题目大意
给定一个染着黑白色的 \(n \times m\) 的网格,每次可以选择一个黑色格子,把这个格子同行或者同列的格子全部染黑,问把 \((r,c)\) 染黑的最小操作次数。
1.2 数据范围
对于 \(100\%\) 的数据:
-
\(1 \leq n, m \leq 50\)
-
\(1 \leq r \leq n\)
-
\(1 \leq c \leq m\)
2 解题分析
玩一下样例后注意到情况很少,于是开始分类讨论。
-
当棋盘上没有黑色格子时,答案无解。
-
当 \((r, c)\) 为黑色时,答案为 \(0\)。
-
当第 \(r\) 行 或第 \(c\) 列有格子为黑色时,答案为 \(1\)。
-
否则,答案为 \(2\)。
这需要解释吗,过于显然了
3 AC Code
void solve() {
cin >> n >> m >> r >> c;
f (i, 1, n)
cin >> a[i] + 1;
bool flag = false;
bool flag2 = false;
f (i, 1, n)
f (j, 1, m) {
if (a[i][j] == 'B'){
flag = true;
if (i == r || c == j)
flag2 = true;
}
}
if (!flag) printf("-1\n");
else if (a[r][c] == 'B') printf("0\n");
else if (flag2) printf("1\n");
else printf("2\n");
}
4 赛后总结
此题我的看题速度很慢,看了很久才懂得题意,玩了一会样例才开始写,一眼盯真的能力读题能力和实践能力需要提升。
B. Not Sitting
0 鲜花
非常好题目,爱来自 CF。
我需要提升一眼盯真的能力。
1 题目大意
1.1 题目大意
有一个 \(n \times m\) 的网格,里面有 \(k\) 个网格被 Tina 染了色。Rahul 先选座位,他不能选染了色的座位。Tina 在 Rahul 之后选座位,他可以随便选。Rahul 想要和 Tina 坐的尽量近,但 Tina 想与 Rahul 坐的尽量远。问对于每一个 \(0 \leq k \leq n \times m - 1\),Rahul 与 Tina 的距离为多少。
注意:上文的距离指曼哈顿距离。
1.2 数据范围
对于 \(100\%\) 的数据:
- \(2 \leq n \cdot m \leq 10^5\)
2 解法分析
第一眼发现不会。于是就开始玩样例。
考虑下面的情况:

显然,当 \(k = 0\) 时,答案为这个。
那如果 \(k = 1\) 呢?那么 Tina 肯定要把原来 Rahul 的位置染色,否则 Rahul 一定会选择原来的位置。
所以每个不同的 \(k\) 所对应 Rahul 的位置是不同的。
到现在,我们不难想到计算出 Rahul 在 \((x,y)\) 时的答案。那么,因为答案是最大哈密顿距离,所以 Tina 的最优策略一定是选择 \((1,1),(1,m),(n,1), (n,m)\) 之中的一个点。直接枚举即可。
于是,预处理出每个 \((x,y)\) 的答案后,对它们组成的数组进行排序再输出即可。
3 AC Code
struct Node {
int x, y;
int maxdis;
bool operator < (const Node &x) const {
return maxdis < x.maxdis;
}
}t[maxn];
int get(int x, int y, int a, int b) {
return abs(x - a) + abs(y - b);
}
void solve() {
cin >> n >> m;
f (i, 1, n)
f (j, 1, m) {
int col = (i - 1) * m + j;
t[col].x = i, t[col].y = j;
t[col].maxdis = max({get(i, j, 1, 1), get(i, j, 1, m), get(i, j, n, 1), get(i, j, n, m)});
}
sort(t + 1, t + n * m + 1);
f (i, 1, n * m)
printf("%lld ", t[i].maxdis);
printf("\n");
}
4 赛后总结
这题我的赛场表现还算满意,马上就想出来了正解。甚至比我 A 想到正解的速度还快。
但读题速度还是太慢了。
C. Not Assigning
0 鲜花
用复杂做法吃了一发罚时,改成简单做法就过了。
我是什么成分的弱智。
1 题目大意
1.1 题目大意
给你一颗 \(n\) 个结点的树,你需要对每条边赋权值,使得任意一条边权或者任意两条相邻边权权值之和为素数。输出一种构造方案。注意:赋的边权 \(w\) 要满足 \(w \leq 10^5\)。
1.2 数据范围
对于 \(100\%\) 的数据:
- \(1 \leq n \leq 10^5\)
2 解法分析
2.1 题目直觉
一看到素数立马想到 \(2\)。但先别急,玩一下样例。
考虑下面的一棵树:
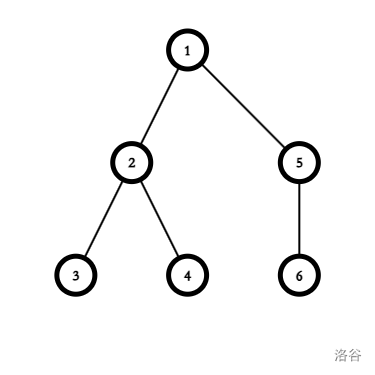
试了一下,发现它好像不行。为什么呢?
再考虑下面的一棵树:
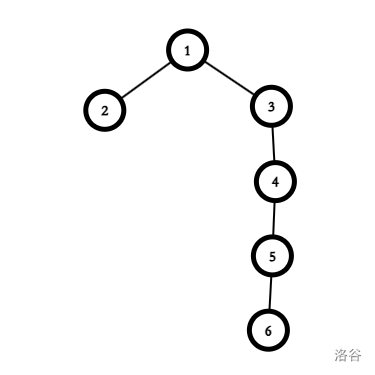
它好像可以,比如说依次填:\(2 \ 3 \ 2 \ 3 \ 2\) 或者 \(2 \ 5 \ 2 \ 5 \ 2\) 都可以,但是 \(2 \ 7 \ 2 \ 7 \ 2\) 不行。
我们到这里就发现了一个规律:树一定要是一条链,此时依次填入 \(2\) 和一个满足 \(p_i\) 为素数且 \(p_i+2\) 为素数的 \(p_i\) 即可。以下统称满足这种性质的素数集合为 \(p\)。
2.2 证明
考虑证明。一般这种题都要分析奇偶性质。知周所众,\(2\) 是唯一一个偶质数。如果相邻两条边都填 \(>2\) 的奇质数,那么它们两个数加起来一定是一个 \(\geq4\) 的偶数,显然是合数,不满足题意。所以我们得知答案一定得是 \(2\) 和 \(p\) 中的某一个数。
然后再来分析为何只能是链。反证法,如果这个树不是链,则一定能找到一个点 \(x\),使得连接它的边超过 \(2\) 条。设连接这个点且边权为 \(2\) 的边权集为 \(w_1\),其他边权集为 \(w_2\),那么由鸽笼原理,必有 \(|w_1| \geq 2\) 或者 \(|w_2| \geq 2\)。分类讨论:
-
如果 \(|w_1| \geq 2\),则 \(2 + 2 = 4\) 为合数,矛盾。
-
如果 \(|w_2| \geq 2\),则它们两个数加起来一定是一个 \(\geq4\) 的偶数,显然是合数,矛盾。
综上所述,满足要求的树只能是链。
3 AC Code
bool dfs(int u, int fa, int ty) {
int pcnt = 0, wcol = -1;
for (auto v : to[u])
if (v.first != fa)
pcnt ++, wcol = v.second;
if (pcnt > 1)
return false;
if (pcnt == 0) return true;
w[wcol] = (ty == 0 ? 2 : 3);
for (auto v : to[u])
if (v.first != fa)
return dfs(v.first, u, ty ^ 1);
return true;
}
void solve() {
cin >> n;
f (i, 1, n) {
to[i].clear();
deg[i] = 0;
}
f (i, 1, n - 1) {
int u, v;
cin >> u >> v;
to[u].push_back({v, i}); deg[v] ++;
to[v].push_back({u, i}); deg[u] ++;
}
int pos = -1;
f (i, 1, n) {
if (deg[i] > 2) {
printf("-1\n");
return ;
}
if (deg[i] == 1) pos = i;
}
bool flag = dfs(pos, -1, 0);
if (!flag) {
printf("-1\n");
return ;
}
f (i, 1, n - 1)
printf("%lld ", w[i]);
printf("\n");
}
4 赛后总结
不要把题目给想复杂。
不要把题目给想复杂。
不要把题目给想复杂。
怎么个想复杂法呢,我自作聪明把 \(\leq 10^5\) 且满足 \(p + 2\) 与 \(p\) 均为素数的所有数都给筛出来,然后轮换着填。结果素数不够。然后就 WA 了。
D. Not Adding
0 鲜花
赛场上以为 \(\mathcal{O}(168n)\) 能过,就去写这个做法了。T 了。结果正解就几行。
警钟敲烂。
1 题目大意
1.1 题目大意
给定一个 \(a\),你可以从 \(a\) 中选择两个数求 \(g = \gcd(x, y)\),如果 \(g\) 不在数组中就加到数组里。问最多可以加几个数。
1.2 数据范围
对于 \(100\%\) 的数据:
-
\(1 \leq n \leq 10^6\)
-
\(1 \leq a_i \leq 10^6\)
2 解法分析
一看到这个题。\(\gcd\)??再一看数据范围。\(a_i \leq 10^6\)??于是你就发现很怪。\(\gcd\) 一般不和值域有关。
这说明此题的复杂度与 \(a_i\) 有关。
于是很容易想到枚举一个数 \(x\),然后判断是否能通过 \(\gcd\) 操作得到即可。
很容易总结出两点:
- \(x\) 要没有在 \(a\) 中出现过。
- \(x\) 的倍数在 \(a\) 中需要超过 \(2\) 个。
于是我们兴高采烈的开始写代码,结果 WA 了。于是开始想有没有 Conser Case。于是继续玩样例。
还真有!考虑下面的数据:
2
20 40
显然,它不可能变出其他可能的值,所以答案是 \(0\)。但是当我们的程序跑到 \(x = 10\) 时,我们发现前两条规则都满足!Why?
于是,不难发现第三条规则:
- \(x \geq \gcd(b_1, b_2, \cdots, b_m)\),其中 \(b\) 是所有在 \(a\) 中的 \(x\) 的倍数的集合。
综上所述,这道题就完成了。
3 AC Code
int mygcd(int x, int y) {
return y == 0 ? x : mygcd(y, x % y);
}
void solve() {
cin >> n;
f (i, 1, n) {
scanf("%lld", &a[i]);
vis[a[i]] = 1;
}
int ans = 0;
f (i, 1, 1e6) {
if (vis[i]) continue;
int p = 0;
for (int j = i * 2; j <= 1e6; j += i)
if (vis[j])
p = mygcd(j, p);
if (p <= i && p != 0) ans ++;
}
printf("%lld\n", ans);
}
5 赛后总结
同鲜花。正解就几行。
多想 \(1\) 分钟,少些 \(2\) 分钟的代码。
E. Not Escaping
1 题目大意
1.1 题目大意
给你一个 \(n \times m\) 的网格图,假设你现在在第 \(x\) 行:
-
你可以移动到第 \(x\) 行的任意其他格点,代价为移动的距离 \(\times a_x\)。
-
你可以通过梯子爬到另外一个格点,设这是第 \(i\) 个梯子,则价值为 \(h_i\)。梯子保证是往上爬的,换句话说,如果你从 \((i,j)\) 爬到了 \((x,y)\),那么保证 \(x > i\)。
问你如果从 \((1,1)\) 走到 \((n,m)\) 所需要的最少代价为多少。
注意:价值 \(\neq\) 代价,价值为 \(+\),代价为 \(-\)。
1.2 数据范围
对于 \(100\%\) 的数据:
-
\(1 \leq n, m \leq 10^5\)
-
\(1 \leq k \leq 10^5\)
2 解法分析
读题的过程中容易发现一个很奇怪的点:
如果你从 \((i,j)\) 爬到了 \((x,y)\),那么保证 \(x > i\)。
仔细一看,这不就相当于一个无后效性的保证吗?但是我们再一看操作 \(1\):行内进行。我们就知道,这个无后效性仅仅在行上得到了保证。所以我们可以很容易的想到按照行为顺序进行 dp。
但是我们又发现:\(1 \leq n, m \leq 10^5\)!这玩个毛啊。所以我们得先把点数的问题处理好,排除一些无效点。
继续观察数据范围,发现 \(k\) 的范围很正常,而且似乎我们只需要考虑梯子两端的顶点,出发点 \((1,1)\) 与终点 \((n, m)\)。这样一来,有效点的数量被压缩成了 \(2 \times k + 2\) 个,看起来很合理。
回到 dp。我们把每个有效点以第一关键字 \(x\),第二关键字 \(y\) 进行排序,然后行内从左到右,从右往左分别扫一遍,最后跨行更新梯子即可。时间复杂度 \(\mathcal{O}(k\log k)\)。
3 AC Code
其实代码可读性还可以,就是太长了。
struct Node {
int x, y, id;
vector <pair <int, int> > ladder;
bool operator < (const Node &p) const {
return x != p.x ? x < p.x : y < p.y;
}
}t[maxn * 2];
void solve() {
cin >> n >> m >> k;
f (i, 1, n)
scanf("%lld", &x[i]);
f (i, 1, k)
scanf("%lld %lld %lld %lld %lld", &a[i], &b[i], &c[i], &d[i], &h[i]);
f (i, 1, 2 * k + 2)
t[i].ladder.clear();
tot = 0;
f (i, 1, k) {
++ tot; t[tot] = {a[i], b[i], tot};
++ tot; t[tot] = {c[i], d[i], tot};
t[tot - 1].ladder.push_back({tot, h[i]});
}
++ tot; t[tot] = {1, 1, tot};
++ tot; t[tot] = {n, m, tot};
sort(t + 1, t + tot + 1);
f (i, 1, tot)
mp[t[i].id] = i;
f (i, 1, tot)
for (auto &x : t[i].ladder)
x.first = mp[x.first];
f (i, 1, n)
row[i].clear();
f (i, 1, tot)
row[t[i].x].push_back(i);
f (i, 1, tot)
dp[i] = 2e18;
dp[1] = 0;
f (i, 1, n) {
f (j, 1, (int) row[i].size() - 1) {
int p = row[i][j - 1];
int q = row[i][j];
dp[q] = min(dp[q], dp[p] + abs(t[p].y - t[q].y) * x[i]);
}
g (j, (int) row[i].size() - 1, 1) {
int p = row[i][j - 1];
int q = row[i][j];
dp[p] = min(dp[p], dp[q] + abs(t[p].y - t[q].y) * x[i]);
}
for (int p : row[i])
for (auto q : t[p].ladder)
dp[q.first] = min(dp[q.first], dp[p] - q.second);
}
if (dp[tot] >= 1e18) printf("NO ESCAPE\n");
else printf("%lld\n", dp[tot]);
}