CNN 卷积神经网络

1. 二维卷积公式（机器学习）

\[O(i, j) = \sum^{kh}_{i = 0} \sum^{kw}_{j = 0} w(i, j) * I(i + kh, j + kw) \]

上述公式中，\(O\) 为输出矩阵，\(I\) 为输入矩阵，\(w\) 为卷积核，\(kh, kw\) 分别为卷积核的高度和宽度，代表着卷积核的大小。

PS：数学中的卷积和卷积神经网络中的卷积严格意义上是两种不同的运算。卷积神经网络的卷积本质上是一种spatial filter，是互相关运算。简单地说，在机器学习中，卷积核不进行翻转；在数学中，卷积核需要进行翻转。

2. LeNet-5 模型

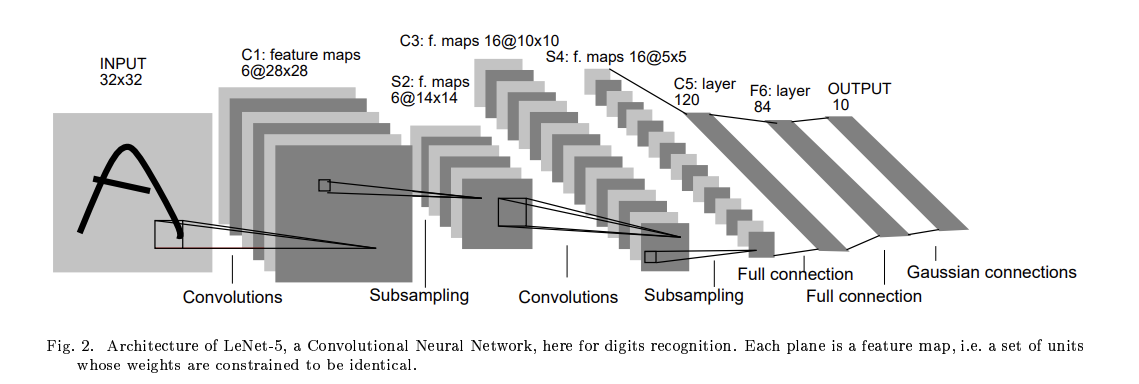
2.1 LeNet-5 的基本结构

公式

令输入矩阵 \(I\) 的大小为 \((H, W)\)，滤波器（卷积核）的大小为 \((kh, kw)\)，输出矩阵 \(O\) 的大小为 \((OH, OW)\)，填充为 \(P\)，步长为 \(S\)。由此输出矩阵大小公式如下：

\[\begin{align} OH &= \frac{H + 2P - kh}{S} + 1 \\ OW &= \frac{W + 2P - kw}{S} + 1 \end{align} \]

INPUT 输入层
输入一张 \(32 \times 32\) 的图片。通常会对输入图像进行预处理（例如像素值归一化）
卷积层 C1
输入大小：\(32 \times 32\)
卷积核种类数：\(6\)
卷积核大小(kh, kw)：\(5 \times 5\)
填充(P)：\(0\)
步长(S)：\(1\)
由此，每个卷积核产生一个 \(28 \times 28\) 的特征图，共 \(6\) 个特征图，神经元数量：\(28 \times 28 \times 6\)
采样层 S2
输入大小：\(28 \times 28\)
采样区域：\(2 \times 2\)
采样方式：Max Pooling 最大池化
步长：\(2\)
由此，输出的 \(6\) 个特征图的大小为 \(14 \times 14\)，神经元数量：\(14 \times 14 \times 6\)
卷积层 C3
输入大小：\(14 \times 14\)
卷积核种类数：\(16\)
卷积核大小(kh, kw)：\(5 \times 5\)
填充(P)：\(0\)
步长(S)：\(1\)
由此，每个卷积核产生一个 \(10 \times 10\) 的特征图，共 \(16\) 个特征图，神经元数量：\(10 \times 10 \times 16\)
采样层 S4
输入大小：\(10 \times 10\)
采样区域：\(2 \times 2\)
采样方式：Max Pooling 最大池化
步长：\(2\)
由此，输出的 \(16\) 个特征图的大小为 \(5 \times 5\)，神经元数量：\(5 \times 5 \times 16\)
全连接层 C5
C5将每个大小为 \(5 \times 5\) 的特征图拉成一个长度为400的向量，并通过一个带有120个神经元的全连接层进行连接。120是由LeNet-5的设计者根据实验得到的最佳值。
全连接层 F6
输入大小：输入的 \(120 \times 1\) 的向量
计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过\(\text{sigmoid}\) 函数输出
由此输出一个 \(84 \times 1\) 的向量
全连接层 Output
共有 \(10\) 个神经元，分别代表数字 0~9。当神经元 \(i\) 的值为0，则表明识别的结果为数字 \(i\)。采用的是径向基函数(RBF)的网络连接方式。

3. CNN计算示例

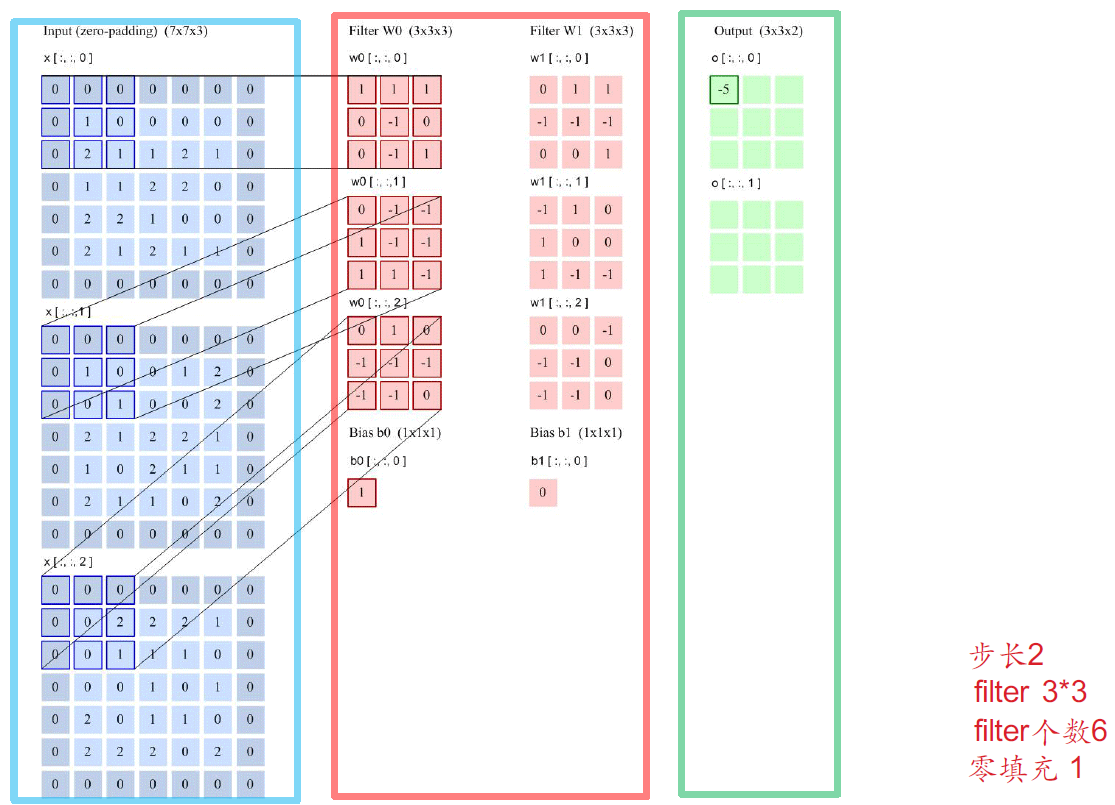
3.1 Conv2d 卷积

\[O(;, ;, 0) = \sum^{kh}_{i = 0} \sum^{kw}_{j = 0} w(i, j, 0) * I(i + kh, j + kw, 0) \]

以计算O(0, 0, 0) 为例

\[O(0, 0, 0) = ((-1) \times 1 + (-1) \times 2 + 1 \times 1) + (-1 \times 1 + (-1) \times 1) + (-1 \times 2) + 1 = -5 \]

3.2 ReLU 非线性激活

\[f_{ij} = \begin{cases} 0, & f_{ij} \le 0 \\ f_{ij}, & f_{ij} > 0 \end{cases} \]

3.3 Pooling 池化（欠采样/下采样）

一般的有：

Max Pooling 最大池化：即每个块里取最大的作为输出的对应元素
Average Pooling 平均池化：即计算每一块的平均值作为输出的对应元素

4. LeNet-5 模型代码

#加载库
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision.datasets as datasets
import torchvision.transforms as transforms

# 定义LeNet-5模型
class LeNet5(nn.Module):
    def __init__(self):
        super(LeNet5, self).__init__()
        # C1
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1) 
        # S2
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
        # C3
        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)
        # S4
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # C5
        self.fc1 = nn.Linear(in_features=16 * 5 * 5, out_features=120)
        # F6
        self.fc2 = nn.Linear(in_features=120, out_features=84)
        # Output
        self.fc3 = nn.Linear(in_features=84, out_features=10)
        
    def forward(self, x):
        x = self.pool1(torch.relu(self.conv1(x)))
        x = self.pool2(torch.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        x = self.fc3(x)
        return x

5. Softmax 和 LogSoftmax

5.1 Softmax

torch.nn.Softmax(dim = 1)

'''
dim = 0: 对每一列的所有元素进行softmax，使得每一列元素和为1
dim = 1: 对每一行的所有元素进行softmax，使得每一行元素和为1
'''

当 \(\text{dim} = 1\) 时的公式：

\[\text{Softmax} ( x) = \frac{e^{ x}}{<e^{ x}, 1 _d>} = \frac{[e^{x_0}, e^{x_1}, ... ,e^{x_{d - 1}}]}{\sum_{j = 0}^{d - 1} e^{x_j}} \]

由此可以看出每个元素的值域为 \((0, 1)\)。

但是，在计算过程中，由于存在指数运算，所以可能会导致数值过大，造成 上溢出；也有可能由于数值小数位靠后，精确度不够，导致四舍五入变为0，此时就造成了 下溢出。

5.2 LogSoftmax

torch.nn.LogSoftmax(dim = 1)

公式：

\[\begin{split} \text{LogSoftmax}( x) &= \text{log}\frac{e^{ x}}{<e^{ x}, x _d>} \\ &= \text{log}[e^{x_0}, e^{x_1}, ... , e^{x_{d - 1}}] - \text{log} \sum_{j = 0}^{d - 1}e^{x_j} \\ &= [x_0 - \text{log}\sum_{j = 0}^{d - 1}e^{x_j}, ..., x_{d - 1} - \text{log}\sum^{d - 1}_{j = 0} e^{x_j}] \end{split} \]

由此可以看出，每个元素的映射到的值域为 \((-\infty, 0)\)。而且由于是对 \(e^x\) 进行对数运算，所以不会造成 \(\text{log}(0)\) 的情况，所以并不用担心负无穷的情况。