ABC267G Increasing K Times
一道计数题.
主要是是一个比较经典的trick才来做的这题.
就是形如已知一个序列,求有多少个排列满足一个条件,这个条件一般是制约相邻两个元素的
那么可以采用一个技巧就是序列排序,然后按照某种顺序插入
考虑有多少排列问题,那么可以先对\(a\) 排序然后依次插入。
每次插入一个最大值,那么只需要求有多少个位置满足插入后满足条件的位置 \(+1\),然后直接跑一遍简单的背包即可。
ARC148E ≥ K
一道计数题。
对于这种对相邻两个元素都有影响的问题,可以考虑将元素按一定顺序一个个加入序列,考虑其对整个方案数的贡献。
1.先将元素从小到大排序。
2.考虑两个维护左右区间的指针 \(l,r\),令 \(a_r\) 为 \(a_l+a_r\geq k\) 的最小编号,其中 \([1,l-1]\) 以及 \([r+1,n]\) 这两段中的元素都已经加入序列。
这样就可以知道一共加入了 \(n-r+l-1\) 个元素,有 \(n-r+l\) 个空位可供下一个元素放置。
-
放入 \(a_r\)
此时一共有 \(l-1\) 个元素无法满足将 \(a_r\) 放入其左边或者右边时无法满足 $ \geq k$的要求(之所以是 \(l-1\) 是因为既然 \(r\)并没有在 \(l\) 之前的元素遍历到时就放入,那么自然前面的元素也是不满足条件的);
那么此时就有 \((n-r+l)-2 \times (l-1)\) 个空位可选。
-
放入 \(a_l\)
\([1,l-1]\) 中的元素和 \(a_l\) 也不能满足条件;
不会有 \(a_l+a_{l-1} \geq k\) ,因为如果这样的话 \(a_l\)就会在遍历到 \(l\) 还是 \(l-1\) 是就被当作 \(a_r\) 放入;
同理,有 \((n-r+l)-2\times(l-1)\) 个空位可选。
-
注意,因为有相同元素,因此要在最后除以相同元素的排列数以消除影响。
LG T316869 Before I Rise
一道计数题.
简化题意之后就是将一个只有环和链,边的种类为0,1交替的图,求满足交换节点之后图仍不变的排列数
先考虑某个环或链自身的交换方案数
1.环
在每个环内部交换的方案数为环的 \(size\)
2.链
节点数为奇数的链自身只有1种
偶数有2种
接下来考虑同种形态之间的排列,就是求排列数即可
但是需要注意分类,对于节点数为偶数的链还需要分为两种形态,例如
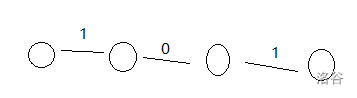
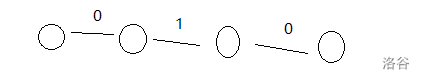
这两种是不能交换的
定义 \(a_i\) 为节点数为 \(i\) 的环, \(b_{i,0/1}\) 为长度为 \(i\) 的第一条边为 \(0/1\) 的链
所以有最后的公式
\(ans=\prod i^{a_i}*(a_i)!*\prod_{i/2\in Z}(b_{i,0})!*(b_{i,1})!*2^{b_{i,0}+b_{i,1}}*\prod_{(i+1)/2\in Z} (b_{i,0}+b_{i,1})!\)
LG3349 [ZJOI2016]小星星
将问题抽象化:
一个 \(n\) 个节点的树,和一个 \(n\) 个节点的图,要求给树上的每个节点编号,使得编号是一个 \(1\)到 \(n\) 的排列,并且要满足树上任意一条边 \((u,v)\),图中一定要有边 \((x_u,x_v)\)( \(x_u\) 表示点 \(u\) 的编号),求方案数。
暴力的做法是定义状态 \(f[i][j][S]\) 表示节点 \(i\) 编号为 \(j\),\(i\) 的子树内的编号集合为 \(S\) 的方案数。
但是这样的瓶颈在于枚举子集,复杂度是 \(O(n^3\times 3^n)\) 的,显然TLE。
Q:为什么要记录 \(S\) 这一维?
A:要求中有「编号是一个 \(1\) 到 \(n\) 的排列」。
尝试把「编号是一个 \(1\) 到 \(n\) 的排列」这一条件去掉,就不用记录 \(S\) 了。
这样只需要定义 \(f[i][j]\) 为在 \(i\) 的子树内,点 \(i\) 的编号为 \(j\) 的方案数。
而这时候会出现重复编号,怎么办呢?
容斥!
先 \(2^n\)枚举 \(\{1,2,...,n\}\) 的一个子集 \(S\),强制规定树上每个点的编号必须是 \(S\) 的子集,然后每次 \(O(n^3)\) 一次DP,总方案数为:
\((∣S∣=n(|S|=n的方案数)−(∣S∣=n−1)-(|S|=n-1的方案数)+(∣S∣=n−2)+(|S|=n-2的方案数)−...)-...\)
复杂度降到 \(O(n^3\times 2^n)\) ,在UOJ上需要进行一定的常数优化。