算是水紫,不过也学到一些有用的东西。
题意
给定正小数 \(N\)。求分子不大于 \(n\),分母不大于 \(m\) 的分数 \(\dfrac{n}{m}\),使得 \(\dfrac{n}{m}\) 的值与 \(N\) 最接近(这里的最接近指的是 \(|\dfrac{n}{m} - N|\) 最小)。
分析
首先,大部分人都可以想到一个暴力:枚举 \(i \in [1, m]\) 作为分子,计算出最佳分母 \(r_1 = \lfloor i \times N \rfloor, r_2 = \lceil i \times N\rceil\)。把 \(r_1, r_2\) 分别带进去看看那个更优就完事了。出去判边界之类的问题,复杂度 \(O(m)\)。由于 \(m \leq 10 ^ 7\),直接就艹过去了。如果这个都不会写可以看这里:暴力算法。
然而我们肯定不会满足于这样的暴力算法。来点优雅的算法吧。
引入分数逼近。这里的分数逼近是指用用一个分数来逼近另一个分数,使得误差趋于零。例如,假设需要逼近的分数为 \(\dfrac{r}{s}\),有分数 \(\dfrac{u}{v} > \dfrac{r}{s}\)。那么有以下结论:
具体等号能不能取到记不清了,不过不影响。结论很好证明,下面证一下。
将 \(\dfrac{r + u}{s + v}\) 与 \(\dfrac{r}{s}\) 做减法,得到 \(\dfrac{r + u}{s + v} - \dfrac{r}{s} = \dfrac{(r + u)s - r(s + v)}{s(s + v)} = \dfrac{us- vr}{s(s + v)}\)。
因为 \(\dfrac{r}{s} < \dfrac{u}{v}\),两边同时乘以 \(sv\),得 \(vr < us\),即 \(us - vr > 0\)。
又因为 \(s(s + v) > 0\),所以 \(\dfrac{us - vr}{s(s + v)} > 0\)。证毕。
注意上面结论和证明成立的条件是 \(u, v, s, r > 0\)。
接下来引入 Stern-Brocot 树这个概念。
Stern-Brocot 树可以维护所有的正分数。这一点可以被我们用来解决这道题目。
首先介绍一下 Stern-Brocot 树。这个树由 \(\dfrac{0}{1}\) 和 \(\dfrac{1}{0}\) 两个分数开始。\(\dfrac{1}{0}\) 不大好定义,暂且把它当做 \(+ \infty\)。将这两个分数作为源节点。
接下来,像我们刚才讨论的分数逼近,将 \(\dfrac{0}{1}\) 和 \(\dfrac{1}{0}\) 的分子分母分别相加,得到另外一个分数 \(\dfrac{1}{1}\)。这个分数确实在 \(\dfrac{0}{1}\) 与 \(\dfrac{1}{0}\) 之间。\(\dfrac{1}{1}\) 被成为第 \(1\) 层迭代后的节点。
同样的,将 \(\dfrac{1}{1}\) 与 \(\dfrac{0}{1}, \dfrac{1}{0}\) 分别进行操作,得到两个分数,称为第二次迭代。
所以我们得到了 Stern-Brocot 树的构建基础:将 \(\dfrac{a}{b}\) 与 \(\dfrac{c}{d}\) 分子分母分别相加,得到 \(\dfrac{a + c}{b + d}\) 作为下一轮迭代的节点。
例如,进行三次操作后,这棵树就会变成这样:
注意,某些节点(就是第 \(i\) 层存在,第 \(i + 1\) 层也存在的节点),实际上在第 \(i + 1\) 层是不会出现的。只是为了方便比较加了上去。
可以看到,第三层的第二个分数 \(\dfrac{1}{3}\) 就是左右两边两个数分子分母分别相加的和。第四个,第六个和第八个以此类推。
下面是来自 OI-wiki 的一张图。
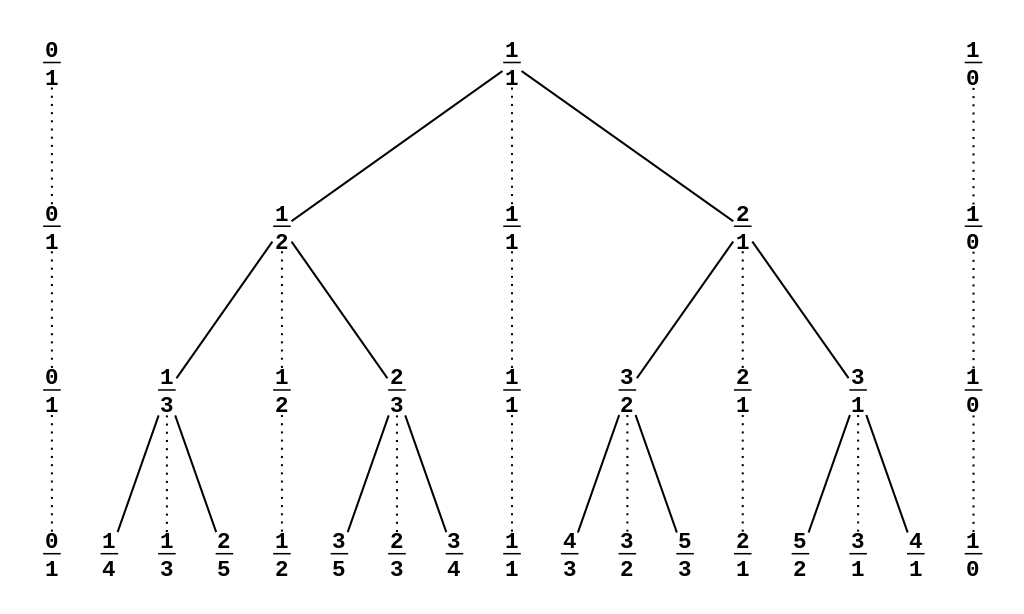
刚才所提到的不存在的节点就是虚线相连的那些节点。可以看到,这棵树具有二叉结构。因此在这棵树上搜索只需要花费 \(O(\log_2 n)\) 的时间。非常优秀。这样对于这道题,我们就可以把小数 \(N\) 从第一层开始向下搜索。如果当前节点值大于 \(N\),那么向左递归。否则向右递归,直到分子或分母大于 \(n\) 或 \(m\)。时间复杂度肯定是 \(O(\log n)\)。(假设 \(n, m\) 同阶)。
关于最简性的证明可以看 OI-wiki 上的解释。这里不再赘述。
这道题的思路就讲解完了。注意别忘了判断多解的情况。由于刚才提到,Stern-Brocot 树具有最简性,因此放心的判断当前分数值与 \(N\) 的误差和原来的是否一样就可以了。
卡常顺便卡了个 rank1。欢迎来踩。
代码
#include <algorithm>
#include <cstdio>
using PII = std::pair<int, int>;
double N, m_error;
int n, m;
PII ans(0, 1);
bool flag = false;
double fabs(double x) {
return x < 0 ? -x : x;
}
inline void get(double N, int a = 0, int b = 1, int c = 1, int d = 0) {
int x = a + c, y = b + d;
if (x > n || y > m) return;
double error = (double)x / y - N;
if (fabs(error) == m_error) flag = true;
if (fabs(error) < m_error) {
flag = false; ans = {x, y}; m_error = fabs(error);
if (error == 0) return;
}
if (error < 0) get(N, x, y, c, d);
else get(N, a, b, x, y);
}
int main() {
scanf("%d%d", &n, &m);
scanf("%lf", &N); m_error = N; get(N);
if (flag) puts("TOO MANY");
else printf("%d/%d", ans.first, ans.second);
return 0;
}
明天就是五一劳动节。在这里提前祝大家五一快乐,多多点赞。