题目描述
给你一个 \(n\) 个点 \(n\) 条边的有向图,若选了当前节点,那么当前节点的儿子节点至少有一个不能选。求最多能选多少个点。
具体思路
显然是一棵基环树,因此考虑基环树 dp。
我们先不管环的条件,先考虑朴素的树形 dp。
设 \(f_{x,0}\) 表示 \(x\) 节点不选,最多可以选多少个点,\(f_{x,1}\) 表示 \(x\) 节点选,最多可以选多少个点。
如果 \(x\) 不选的话,那么 \(x\) 的儿子 \(y\) 选或不选都没关系,有:
\[f_{x,0}=\max \limits_{y \in son(x)} \{ {f_{y,0},f_{y,1}} \}
\]
如果 \(x\) 选的话,那么 \(x\) 的儿子里面就一定要有一个点不选,我们枚举这个不选的点,有:
\[f_{x,1}=\max \limits_{y \in son(x)} \{ {f_{y,0}+ \max \limits_{z \in son(x),z \ne y} \{ {f_{z,0},f_{z,1}} \}} \}
\]
显然这个状态转移方程是 \(O(n^2)\) 的,考虑优化。
我们发现 \(\max \limits_{z \in son(x),z \ne y} \{ {f_{z,0},f_{z,1}} \}\) 和 \(f_{x,0}\) 的转移很像,因此考虑用 \(f_{x,0}\) 来表示 \(f_{x,1}\)。
有:
\[f_{x,1}=f_{x,0}+1+\max \limits_{y \in son(x)} \{ {f_{y,0}-\max(f_{y,0},f_{y,1})} \}
\]
我们来理解一下这个式子。
首先,加一是因为你当前选了 \(x\) 这个点,因此贡献要加一。
其次,加上 \(f_{y,0}\) 是因为你 \(y\) 这个点不选,因此要加上它不选的贡献。
然后,我们发现 \(f_{x,0}\) 里面计算了一遍 \(y\) 的贡献,因此我们要将它减去。
最后,我们设的 \(f_{x,1}\) 表示的是最多可以放多少个点,因此要对每个 \(y\) 都取一遍最大值。
现在问题就转换成了如果树上有环,应该如何计算这个环对动态规划的影响。
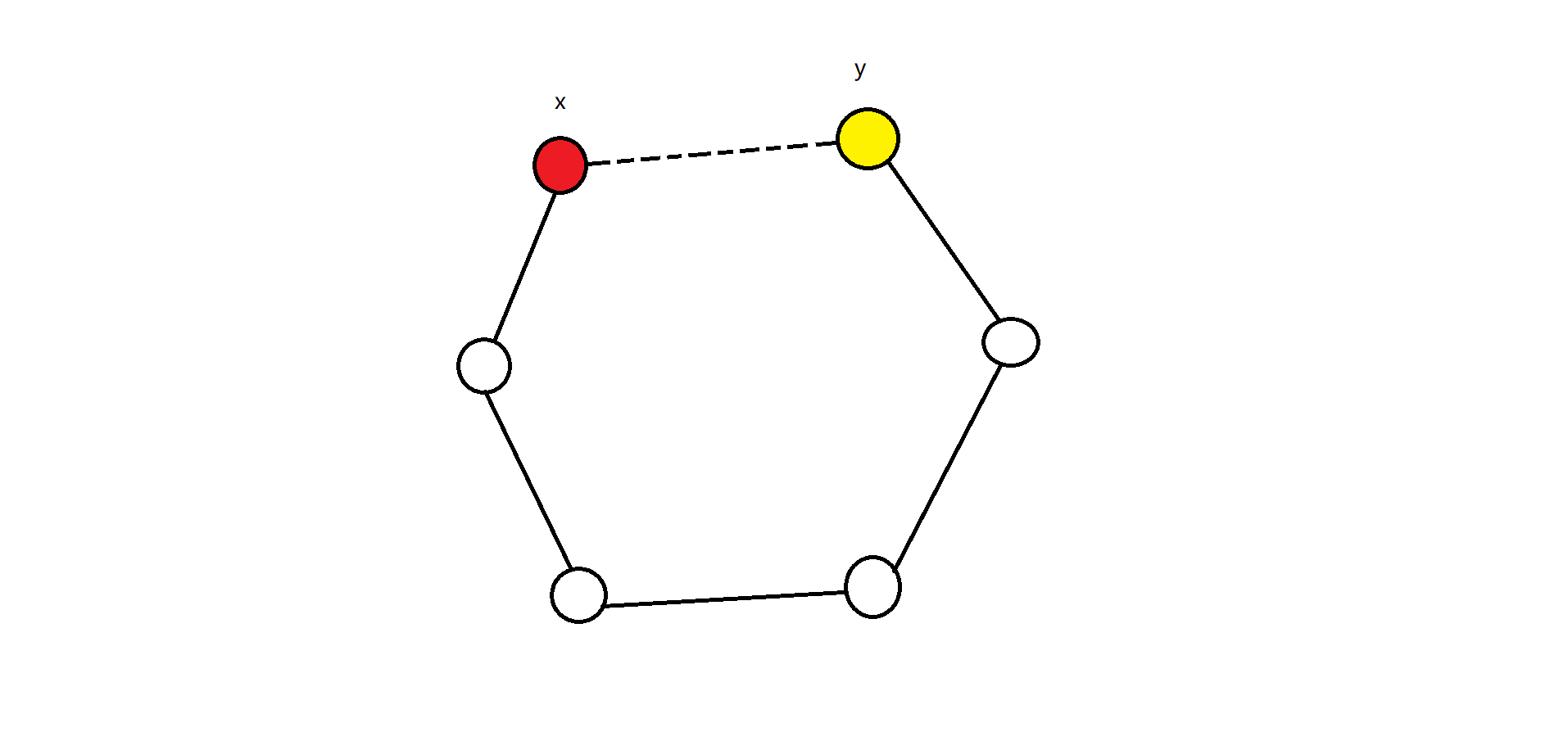
如图所示,\(x\) 和 \(y\) 分别是环的两个端点。
- 若 \(edge(x,y)\) 没有影响
- 若