基本概念
样条:通过一组指定点集而生成的平滑曲线的柔性带。
样条曲线(spline curve):由多项式曲线段连接而成的曲线,在每段的边界处满足特定的连续性条件。
样条曲面(spline surface):用两组样条曲线进行描述曲面。而曲面可以看成一条曲线在空间连续运动形成的轨迹。
插值、逼近样条
给定一组控制点(control points)坐标,描述了曲线大致形状,就得到一条样条曲线。
由概念知,样条曲线关键点,在于选取的多项式在分段连接处,满足特定的连续性条件。有两种方法选取分段连续参数:
1)插值(interpolate):选取的多项式使得曲线经过每个控制点(点都在曲线上)。
所得曲线称为插值样条曲线。插值曲线,常用于数字化绘图,指定动画路径。
2)逼近(approximate):选取的多项式使得部分或全部控制点不在生成的曲线上(至少有一个控制点不在曲线上)。
所得曲线称为逼近样条曲线。逼近曲线,常用作设计工具构造对象形体。
包含一组控制点的凸多边形,称为凸壳(conver hull)。二维曲线的凸壳是一个凸多边形,其形状就像一个围绕控制点的拉紧的橡皮筋,每个控制点都在凸壳内或边界上。
凸壳的作用:
1)提供曲线/曲面与围绕控制点区域间的偏差的测量。
2)样条以凸壳为界,能保证对象形态平滑地沿控制点前进。
3) 限制曲线/曲面的范围。
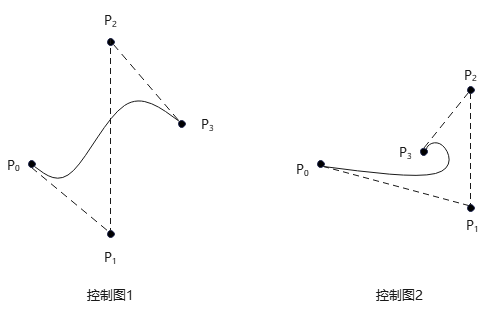
对于逼近样条,按一定顺序用折线连接控制点,这些折线常称为曲线的控制图(control graph),可提醒设计者控制点顺序。
xy平面上两组控制点的凸壳(虚线):

对应控制图(虚线):
参数连续性条件
样条曲线定义中提到,分段曲线满足特定连续性条件。而要保证分段曲线从一段到另一端平滑过渡,可以在连接点处要求各种连续性条件(continuity conditions)。
样条的每一分段,可以用参数坐标表示:
\[\tag{1}
x=x(u),y=y(u),z=z(u),u_1\le u \le u_2
\]
在曲线段连接处,匹配连接的参数导数,从而建立参数连续性(parametric continuity)。
0阶参数连续性(zero-order parametric continuity):记为\(C^0\)连续性,可简单表示曲线相连。第一条曲线段在\(u_2\)处x、y、z坐标与第二条曲线在\(u_1\)处相等。
一阶参数连续性(first-order parameteric continuity):记为\(C^1\)连续性,代表两条相邻曲线段在连接点处一阶导数(切线)相同。
二阶参数连续性(second-order parametric continuity):记为\(C^2\)连续性,代表两条相邻曲线在连接点处一阶、二阶导数相同。
几何连续性条件
几何连续性(geometric continuity)是另一种分段曲线特定连续性条件,与参数连续性条件区别是,只要求分段曲线在相交处的参数导数成比例,而不要求相等。
0阶几何连续性(zero-order geometric continuity):记为\(G^0\)连续性,相邻分段曲线在连接处坐标相同(与\(C^0\)连续性相同)。
一阶几何连续性(first-order geometric continuity):记为\(G^1\)连续性,相邻分段曲线在连接处一阶导数成比例(比例系数为正,代表切线方向相同,模不同)。
二阶几何连续性(second-order geometric continuity):记为\(G^2\)连续性,相邻分段曲线在连接处一阶、二阶导数成比例(比例系数为正)。
三个控制点拟合的2条曲线段,示意参数连续性与几何连续性的区别:
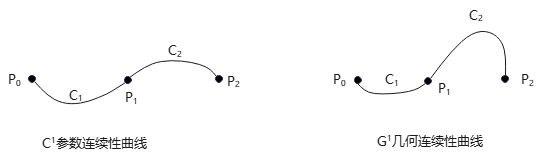
注:在2段曲线连接点\(P_1\)处切线斜率——\(C^1\)参数连续性是斜率相同,\(C^2\)参数连续性是斜率可不同,但成比例。
样条描述
给定多项式阶数、控制点位置后,如何给出具体的样条表达式?
有三种办法:
1)列出一组加在样条上的边界条件;
2)列出样条特征的行列式;
3)列出一组混合函数或基函数(blending functions or basic functions),确定如何组合指定的曲线几何约束,以计算曲线路径上的位置。
下面以三阶多项式为例,说明这三种等价方法。假设沿样条路径有关于x坐标的三次参数多项表达式:
\[\tag{1}
x(u)=a_xu^3+b_xu^2+c_xu+d_x, 0\le u \le 1
\]
曲线的边界条件(4个)可设为端点坐标x(0)、x(1),端点处一次导数x'(0)、x'(1),可用于确定4个参数(也是系数)\(a_x、b_x、c_x、d_x\)。
tips:下面是求4个系数的过程。
\[\tag{2}
\begin{aligned}
&x'(u)=3a_xu^2+2b_xu+c_x\\
&\implies
\begin{cases}
x'(0)=c_x\\
x'(1)=3a_x+2b_x+c_x\\
x(0)=d_x\\
x(1)=a_x+b_x+c_x+d_x
\end{cases}\\
&\implies
\begin{cases}
a_x=x'(1)-2x(1)+x'(0)-2x(0)\\
b_x=-x'(1)+3x(1)-2x'(0)-3x(0)\\
c_x=x'(0)\\
d_x=x(0)\\
\end{cases}
\end{aligned}
\]
将x(u)写成矩阵形式,描述样条曲线:
\[\tag{3}
\begin{aligned}
x(u)&=\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
a_x\\
b_x\\
c_x\\
d_x
\end{bmatrix}\\
&=U\cdot C
\end{aligned}
\]
其中,U是参数u的幂次行矩阵,C是系数列矩阵。
根据前面求系数的过程,可将方程组写成下面形式:
\[\begin{aligned}
d_x&=x(0)\\
a_x+b_x+c_x+d_x&=x(1)\\
c_x&=x'(0)\\
3a_x+2b_x+c_x&=x'(1)
\end{aligned}
\]
转换成矩阵形式:
\[\begin{bmatrix}
0 & 0 & 0 & 1\\
1 & 1 & 1 & 1\\
0 & 0 & 1 & 0\\
3 & 2 & 1 & 0
\end{bmatrix}\cdot\begin{bmatrix}
a_x\\
b_x\\
c_x\\
d_x
\end{bmatrix}=\begin{bmatrix}
x(0)\\
x(1)\\
x'(0)\\
x'(1)
\end{bmatrix}\\
\implies
\begin{bmatrix}
a_x\\
b_x\\
c_x\\
d_x
\end{bmatrix}=M^{-1}\cdot \begin{bmatrix}
x(0)\\
x(1)\\
x'(0)\\
x'(1)
\end{bmatrix}\\
\implies C=M_{spline}\cdot M_{geom} \tag{4}
\]
于是,系数列矩阵C可写成矩阵乘积形式。其中,\(M_{spline}\)是将几何约束转换成多项式系数的4x4矩阵,\(M_{geom}\)是包含样条上的几何约束(边界条件)的1x4列矩阵。
三次样条插值
三次样条:样条的每个曲线段由三次多项式拟合。常用于建立对象运动路径,提供实体表示、绘画,设计物体形状等。
给出一组控制点,拟合这些输入点而生成分段三次多项式曲线,可得到经过每个控制点的三次插值样条。假设有n+1个控制点,坐标:
\[p_k=(x_k,y_k,z_k), k=0,1,2,...,n
\]
n+1个控制点产生n条曲线段,每一段由一对(2个)控制点控制,都可以用下面方程组来描述拟合参数三次多项式:
\[\tag{5}
\begin{aligned}
x(u)&=a_xu^3+b_xu^2+c_xu+d_x\\
y(u)&=a_yu^3+b_yu^2+c_yu+d_y, & 0\le u \le 1\\
z(u)&=a_zu^3+b_yu^2+c_zu+d_z
\end{aligned}
\]
每个三次多项式x(u)、y(u)、z(u)的系数,都可以通过式(3)利用边界条件解出。
自然三次样条
自然三次样条(natrual cubic spline):相邻的曲线段在公共点处具有相同的一阶、二阶导数的三次样条,即具有\(C^2\)连续性。
常用于绘图。
缺点:如果其中一个控制点发生变动,则整条曲线都会受到影响,不允许“局部调整”,需要给出完整的新控制点集。
Hermite插值
Hermit插值样条:分段三次多项式,在每个控制点具有给定的切线。允许局部调整。
如果控制点\(p_k、p_{k+1}\)之间曲线段是参数三次函数\(P(u)\),那么Hermit曲线段边界条件:
\[\tag{6}
\begin{aligned}
P(0)&=p_k\\
P(1)&=p_{k+1}\\
P'(0)&=Dp_k\\
P'(1)&=Dp_{k+1}
\end{aligned}
\]
其中,\(p_k、p_{k+1}\)是给定值,代表曲线段两端点;\(Dp_k、Dp_{k+1}\)是给定值,代表曲线段在端点处一阶导数,即切线斜率。
Hermit曲线段P(u)是三次多项式,因此可写出(5)的等价方程:
\[\tag{7}
\begin{aligned}
P(u)&=au^3+bu^2+cu^1+d, & 0\le u \le 1
\end{aligned}
\]
其中,P(u)由x、y、z 3个分量构成,每个分量都能写成\(x(u)=a_xu^3+b_xu^2+c_xu+d_x\)形式。
式(7)的等价矩阵形式:
\[\tag{8}
P(u)=\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}\cdot \begin{bmatrix}
a\\
b\\
c\\
d
\end{bmatrix}
\]
P(u)的导数可写成:
\[\tag{9}
P'(u)=3au^2+2bu+c=\begin{bmatrix}
3u^2 & 2u & 1 & 0
\end{bmatrix}\cdot \begin{bmatrix}
a\\
b\\
c\\
d
\end{bmatrix}
\]
用0、1替代式(8)(9)中u,可得到Hermit边界条件并写成矩阵形式:
\[\tag{10}
\begin{bmatrix}
P(0)\\
P(1)\\
P'(0)\\
P'(1)
\end{bmatrix}=\begin{bmatrix}
p_k\\
p_{k+1}\\
Dp_k\\
Dp_{k+1}\\
\end{bmatrix}=\begin{bmatrix}
0 & 0 & 0 & 1\\
1 & 1 & 1 & 1\\
0 & 0 & 1 & 0\\
3 & 2 & 1 & 0
\end{bmatrix}\cdot \begin{bmatrix}
a\\
b\\
c\\
d
\end{bmatrix}
\]
求解多项式系数:
\[\tag{11}
\begin{aligned}
\begin{bmatrix}
a\\
b\\
c\\
d
\end{bmatrix}
&=\begin{bmatrix}
0 & 0 & 0 & 1\\
1 & 1 & 1 & 1\\
0 & 0 & 1 & 0\\
3 & 2 & 1 & 0
\end{bmatrix}^{-1}\cdot \begin{bmatrix}
p_k\\
p_{k+1}\\
Dp_k\\
Dp_{k+1}\\
\end{bmatrix}\\
&=
\begin{bmatrix}
2 & -2 & 3 & 1\\
-3 & 3 & -2 & -1\\
0 & 0 & 1 & 0\\
1 & 0 & 0 & 0
\end{bmatrix}\cdot \begin{bmatrix}
p_k\\
p_{k+1}\\
Dp_k\\
Dp_{k+1}\\
\end{bmatrix}\\
&=M_H\cdot \begin{bmatrix}
p_k\\
p_{k+1}\\
Dp_k\\
Dp_{k+1}\\
\end{bmatrix}
\end{aligned}
\]
其中,\(M_H\)是边界矩阵的逆矩阵。
于是,式(8)可写成:
\[\tag{12}
\begin{aligned}
P(u)
&=\begin{bmatrix}
u^3 & u^2 & u & 1
\end{bmatrix}\cdot M_H\cdot \begin{bmatrix}
p_k\\
p_{k+1}\\
Dp_k\\
Dp_{k+1}\\
\end{bmatrix}\\
&=p_k(2u^3-3u^2+1)+p_{k+1}(-2u^3-3u^2)+Dp_k(3u^3-2u^2+u)+Dp_{k+1}(u^3-u^2)\\
&=p_kH_0(u)+p_{k+1}H1+Dp_kH_2+Dp_{k+1}H3
\end{aligned}
\]
多项式\(H_k(u)(k=0,1,2,3)\)称为混合函数。
Bézier 样条曲线
Bézier 样条(Bézier spline,亦称贝塞尔样条)是一种常用样条曲线,能更好用于曲线、曲面设计,也容易实现。
与Hermit曲线区别:不需要导数。
曲线公式
假设给定n+1个控制点坐标:\(p_k(x_k,y_k,z_k)(k=0,1,...,n)\),这些点产生位置向量P(u),用于描述\(p_0、p_n\)之间逼近Bézier多项式函数的路径:
\[\tag{13}
P(u)=\sum_{{k=0}}^n p_kBEZ_{k,n}(u), 0\le u \le 1
\]
Bézier混合函数(或基函数)\(BEZ_{k,n}(u)\)是Bernstein多项式:
\[\tag{14}
BEZ_{k,n}(u)=C(n,k)u^k(1-u)^{n-k}
\]
其中,参数C(n,k)是二项式系数:
\[\tag{15}
C(n, k)={n!\over k!(n-k)!}
\]
tips:二项式\((a+b)^n\)展开第k项系数为C(n,k)(0<=k<=n),称为二项式系数。而Bézier基函数是二项式\((u+(1-u))^n\)的展开式。
将式(13)按x、y、z分量展开,可得:
\[\tag{16}
\begin{aligned}
x(u)&=\sum_{{k=0}}^n x_kBEZ_{k,n}(u)\\
y(u)&=\sum_{{k=0}}^n y_kBEZ_{k,n}(u)\\
z(u)&=\sum_{{k=0}}^n z_kBEZ_{k,n}(u)\\
\end{aligned}
\]
Bézier曲线是阶数比控制点数少1的多项式。
Bézier 混合函数符合递归关系:
\[\tag{17}
BEZ_{k,n}(u)=(1-u)BEZ_{k,n-1}(u)+uBEZ_{k-1,n-1}(u), 1\le k < n
\]
证明:
要使得式子有意义,k需满足0<=k,k-1<=n,取交集1<=k<n
\[\begin{aligned}
右边&=(1-u){(n-1)!\over k!(n-1-k)!}u^k(1-u)^{n-1-k}+u{(n-1)!\over (k-1)!(n-k)!}u^{k-1}(1-u)^{n-k}\\
&=u^k(1-u)^{n-k}(n-1)![{1\over k!(n-1-k)!}+{1\over (k-1)!(n-k)!}]\\
&=u^k(1-u)^{n-k}(n-1)![{n-k\over k!(n-k)!}+{k\over k!(n-k)!}]\\
&=u^k(1-u)^{n-k}{n!\over k!(n-k)!}\\
&=左边
\end{aligned}
\]
二项式系数C(n,k),可以用递推关系来计算:
\[\tag{18}
C(n,k)={n-k+1\over k}C(n,k-1)
\]
如何绘制Bezier曲线?
现已知n+1个控制点\(p_0,p_1,...p_n\)坐标,那么如何绘制出Bezier曲线呢?
Bezier曲线是连续曲线,但要绘制在屏幕上,必须要光栅化,也就是离散化。参数u取值范围[0, n],假设指定要绘制nBezCurvePts=1000个点模拟曲线,那么相邻点u分量\(Δu=n/(float)nBezCurvePts\),即\(u_k=k/(float)nBezCurvePts(k=0,1,2,...,n)\)。
要绘制曲线,也就是要求出P(u)的x、y、z分量。以求x分量为例,根据式(16),\(x_k\)是第k个控制点x分量(已知),问题转化为求\(BEZ_{k,n}(u)\)。
根据式(14),可以分为2部分:
1)二项式系数C(n,k)
可用循环累计乘除方式来求。
2)\(u^k(1-u)^{n-k}\)
可调用数学函数pow求次幂。
OpenGL实现代码参见:bezier示例代码
Bézier曲线特性
\[\tag{19}
P(0)=p_0, P(1)=p_n
\]
证明:
因为u与k都可能为0,因此规定\(0^0=1\)。这样,
\[\begin{aligned}
P(0)&=\sum_{{k=0}}^n p_kBEZ_{k,n}(0)=\sum_{{k=0}}^n p_kC(n,k)0^k1^{n-k}=p_0\\
P(1)&=\sum_{{k=n}}^n p_kBEZ_{k,n}(1)=\sum_{{k=0}}^n p_kC(n,k)1^k0^{n-k}=p_n
\end{aligned}
\]
即得证。
\[\tag{20}
\begin{aligned}
P'(0)&=-np_0+np_1\\
P'(1)&=-np_{n-1}+np_n
\end{aligned}
\]
证明:
可对P(u)展开式求导,但有2种特殊情况:
1)\(u^0, (1-u)^0\)是常数1,求导后不含u项(与u无关)。
2)\(u^1、(1-u)^1\)对u求导后为常数1、-1,不含u项(与u无关)。
因此,展开式需要特别考察第0、1、n-1、n项。
\[\begin{aligned}
P(u)&=p_0C(n,0)u^0(1-u)^n+p_1C(n,1)u^1(1-u)^{n-1}+...+p_{n-1}C(n,n-1)u^{n-1}(1-u)^1+p_nC(n,n)u^n(1-u)^0\\
&=p_0(1-u)^n+p_1nu^1(1-u)^{n-1}+...+p_{n-1}nu^{n-1}(1-u)+p_nu^n\\
P'(u)&=p_0n(1-u)^{n-1}(-1)+p_1n[(1-u)^{n-1}+u(n-1)(1-u)^{n-2}(-1)]+\sum_{{k=2}}^{n-2}p_kC(n,k)[ku^{k-1}(1-u)^{n-k}+u^k(n-k)(1-u)^{n-k-1}(-1)] \\
&+ p_{n-1}n[(n-1)u^{n-2}(1-u)+u^{n-1}(-1)]+p_nnu^{n-1}\\
P'(0)&=-np_0+np_1 (含u项皆为0)\\
P'(1)&=-np_{n-1}+np_n (含1-u项皆为0)
\end{aligned}
\]
即得证。
三次Bézier曲线
图形软件包为兼顾设计方便与计算量,通常支持三次Bézier曲线。对应多项式最高阶数为3,因此控制点数n为4。
4个基函数:
\[\tag{21}
\begin{aligned}
BEZ_{3, 0}&=(1-u)^3\\
BEZ_{3, 1}&=3u(1-u)^2\\
BEZ_{3, 2}&=3u^2(1-u)\\
BEZ_{3, 3}&=u^3
\end{aligned}
\]
P(u)可用混合多项式表示为:
\[\tag{22}
P(u)=c_0+c_1u+c_2u^2+c_3u^3\\
其中, 系数列矩阵c=(c_0,c_1,c_2,c_3)^T
\]
又由前面Bézier曲线特性知:
\[\tag{23}
\begin{aligned}
P(0)&=p_0=c_0\\
P(1)&=p_3=c_0+c_1+c_2+c_3\\
P'(0)&=3p_1-3p_0=c_1\\
P'(1)&=3p_3-3p_2=c_1+2c_2+3c_3
\end{aligned}
\]
可以解出列矩阵c,得到列矩阵c与列矩阵p的关系:
\[\tag{24}
\begin{aligned}
c_0&=p_0\\
c_1&=-3p_0+3p_1\\
c_2&=3p_0-6p_1+3p_2\\
c_3&=-p_0+3p_1-3p_2+p_3\\
<=>
\begin{bmatrix}
c_0\\
c_1\\
c_2\\
c_3
\end{bmatrix}
&=\begin{bmatrix}
1 & 0 & 0 & 0\\
-3 & 3 & 0 & 0\\
3 & -6 & 3 & 0\\
-1 & 3 & -3 & 1
\end{bmatrix}\cdot \begin{bmatrix}
p_0\\
p_1\\
p_2\\
p_3
\end{bmatrix}\\
<=>c&=M_Bp
\end{aligned}
\]
其中,\(M_B\)称为Bézier几何矩阵(Bézier geometry matrix)。
于是,Bézier三次多项式为:
\[\tag{25}
P(u)=(1, u, u^2, u^3)c=u^Tc=u^TM_Bp
\]
参考
Bezier曲线(一):定义与控制点移动
Bezier曲线与B-Spline曲线


