526互联

02_回归问题

发布时间 2024-01-02 20:52:22作者: monarch_bai

回归问题

回归问题为监督学习问题，大多数是以已有的数据建立模型来预测准确的值，一般分为线性回归和非线性回归

一、线性回归

1、举个栗子

以银行贷款额度为例

工资 年龄 额度
4000 25 20000
8000 30 70000
5000 28 35000
7500 33 50000
12000 40 85000
  • 特征x：工资和年龄
  • 目标y：银行贷款额度
  • 参数\(\theta\)：工资和年龄都会影响银行的贷款额度，那他们各自对额度的具体影响权重分别是多少

以上述条件可以简单的得到一个公式:

\(y = \theta_1 x_1 + \theta_2 x_2\)

回归问题的核心，就是求\(\theta\) ，即各个特征对目标值的影响权重，来使公式的预测值尽可能的符合(拟合)实际值

2、通俗解释

可以参考下图理解：

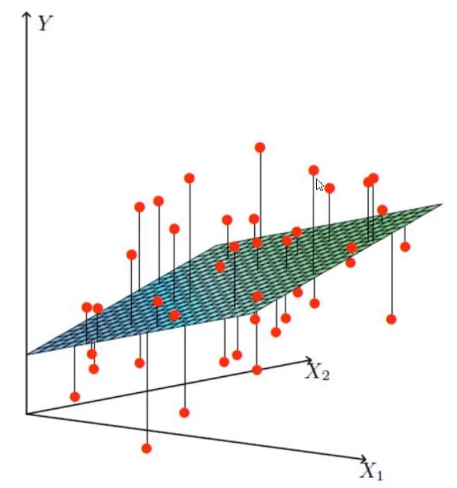
image-20231230205404860

  • \(X_1\)、\(X_2\)就是两个特征
  • Y就是目标值
  • 平面为我们建立的公式模型
  • 各个点为实际的数据

由图可知，在实际的数据中，由于我们这里使用的是线性回归，是没有办法来拟合所有的数据点的，只能力求最大限度的满足更多的数据点

3、数学解释

上面由\(\theta_1\)和\(\theta_2\)已经简单的得到了一个公式，但是还不完整，一般的拟合平面都需要再加上一个偏置项\(\theta_0\) ,从而得到完整的公式：

\(h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2\)

在上述公式中，\(\theta_1\)和\(\theta_2\)一般称之为权重项，对模型起决定作用，而做为偏置项的\(\theta_0\)是对模型进行微调，在权重项不变的情况下，偏置项的变化只会对平面进行上下移动

在引入偏置项后，我们再引入一个数值为1的\(x_0\),，将偏置项改为\(\theta_0x_0\)，从而可整合公式：

\(h_\theta(x) = \sum_{i=0}^{n}\theta_ix_i = \theta^Tx\)

上述公式就转换成了矩阵的形式，在实际数据处理中，大多数都是以矩阵的形式来处理数据

4、误差

真实值和预测值之间肯定是存在差异的(用\(\varepsilon\)表示误差)

那么，对于每个样本：\(y^i = \theta^Tx^i + \varepsilon^i\)

\(y^i\)为真实值，\(\theta^Tx^i\)为预测值，\(\varepsilon^i\)为误差

不同样本的误差是不同的，机器学习建立的模型，就是通过一个目标函数或损失函数，让误差值越小越好，尽可能的接近于零

误差\(\varepsilon^i\)是独立并且具有相同分布，并且服从均值为0方差为\(\theta^2\)的高斯分布(正态分布)

  • 独立：指每个样本之间互不影响，设A，B为随机事件，若同时发生的概率等于各自发生的概率的乘积，例如张三和李四一起来贷款，他们的贷款额度互不影响，没有关系

  • 同分布：具有相同的概率分布，例如张三和李四都是来我们假定的银行贷款

  • 高斯分布(正态分布)：例如银行可能给的多，也可能给的少，但是绝大多数情况下这个浮动都不会太大，大部分都符合正常情况

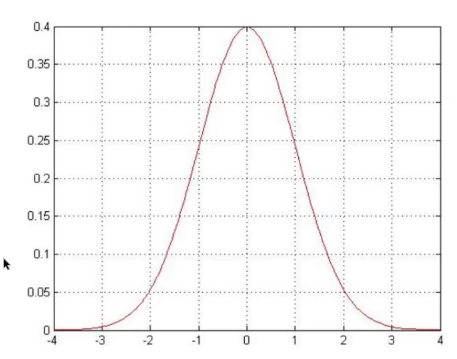
    image-20231230215130078

  • 由于误差服从正态分布，那么可得公式：\(p(\varepsilon^i) = \frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(\varepsilon^i)^2} {2\sigma^2})}\)

  • 将样本公式代入上面的公式得：\(p(y^i|x^i;\theta) = \frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(y^i - \theta^Tx^i)^2} {2\sigma^2})}\)

    \(p(y^i|x^i;\theta)\)为在\(x=x^i,\theta=\theta\)下，\(y=y^i\)的概率，这个概率越大越好

由于每个样本都是独立的，所以每个样本符合预测值概率的乘积，就是所有样本符合预测值的概率，从而引入似然函数和对数似然的概念

  • 似然函数: \(L(\theta)=\prod^m_{i=1}p(y^i|x^i;\theta) = \prod^m_{i=1}\frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(y^i - \theta^Tx^i)^2} {2\sigma^2})}\)

    什么样的参数跟数据组合后能更符合真实值

  • 对数似然：\(logL(\theta)= log\prod^m_{i=1}\frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(y^i - \theta^Tx^i)^2} {2\sigma^2})} = \sum^m_{i=1}log\frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(y^i - \theta^Tx^i)^2} {2\sigma^2})}\)

    在似然函数中，所有概率是相乘的，求解比较困难，而将似然函数取对数，就将乘法转换为加法，更容易求解

之所以能进行对数似然，是因为我们要求的是\(\theta\)这个极值点，而不是\(L(\theta)\)这个极值，所以将\(L(\theta)\)对数化后，并不会改变这个极值点\(\theta\)

  • 将对数似然展开化简:\(\sum^m_{i=1}log\frac 1 {\sqrt{2\pi}\sigma}exp{(-\frac{(y^i - \theta^Tx^i)^2} {2\sigma^2})} = mlog\frac 1 {\sqrt{2\pi}\sigma} - \frac1{\sigma^2}.\frac12\sum^m_{i=1}(y^i - \theta^Tx^i)^2\)

  • 我们的目标是让对数似然函数越大越好，则可让\(J(\theta) = \frac12\sum^m_{i=1}(y^i - \theta^Tx^i)^2\)越小越好

    这个就是我们常用的最小二乘法，上述的\(J(\theta)\)就是我们所说的目标函数或者叫损失函数

5、参数求解

  • 已知目标函数：\(J(\theta) = \frac12\sum^m_{i=1}(y^i - \theta^Tx^i)^2=\frac12\sum^m_{i=1}(h_\theta(x^i)-y^i)^2 = \frac12(X\theta - y)^T(X\theta-y)\)

  • 对函数求\(\theta\)的偏导：

    \(\nabla_\theta J(\theta)=\nabla_\theta [\frac12(X\theta - y)^T(X\theta-y)]=\nabla_\theta[\frac12(\theta^TX^T-y^T)(X\theta-y)]\)

    \(=\nabla_\theta[\frac12(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty)]\)

    \(=\frac12(2X^TX\theta-X^Ty-(y^TX)^T)=X^TX\theta-X^Ty\)

    注：在A为对称矩阵时 \(\frac{\partial x^TAx}{\partial x} = 2Ax\)

  • 让偏导等于0得：\(\theta = (X^TX)^{-1}X^Ty\)

6、梯度下降

上述的推导过程，只是理论情况下，并非机器学习的过程，在实际情况中，我们并不能保证\(X^TX\)可逆，也就不能求解，且机器学习强调的是一个学习的过程，是一个通过数据不断逼近真实值的过程，所以引出了梯度下降的概念

梯度下降是一个优化算法或者说是机器学习中真正的一个求解思路，常规套路就是我们给机器一堆数据和一个目标函数，目标函数规定怎么样学习是对的，然后让机器朝着正确的方向去学习

学习是一个积累的过程，每次优化一点点，一次次的迭代，最后得到好的结果

梯度下降可以看做是一个下山问题

img

img

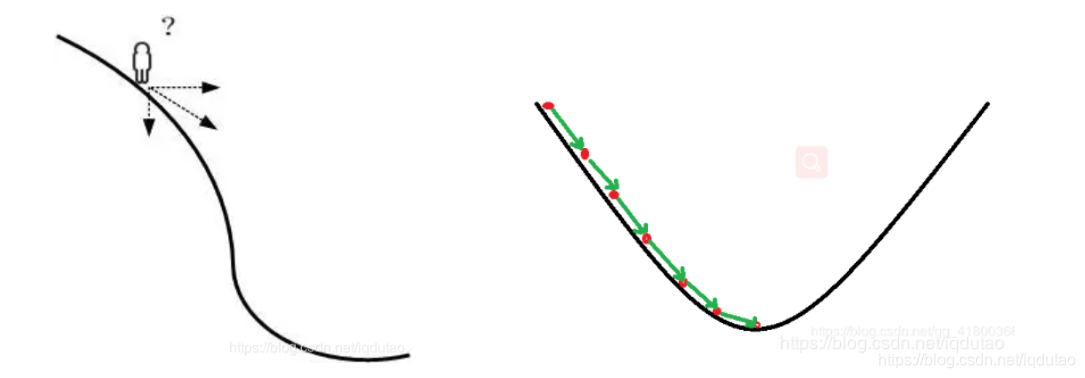
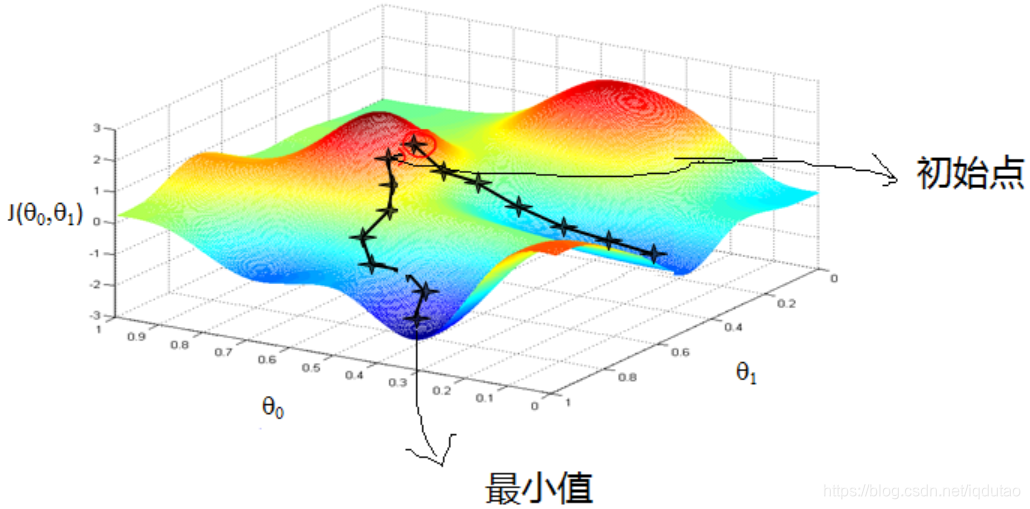
一个人在山坡上时，要朝哪个方向走才能最快到达山底呢？切线方向。所以机器学习中，求解极值点的方法就是，先给定一个初始值，然后在初始值点求导，得到切线方向，然后前进一小步，再求导，每一次求导就更新一次参数，最后到达山底。

  • 梯度下降的目标函数：\(J(\theta) = \frac1{2m}\sum^m_{i=1}(y^i-h_\theta(x^i))^2\)

    注：\((y^i-h_\theta(x^i))\)是误差，m为样本数，平方是为了保证误差为正，且让误差更明显

  • 梯度下降方法：

    • 批量梯度下降：\(\frac{\partial J(\theta)}{\partial \theta_j} = -\frac1m \sum^m_{i=1}(y^i-h_\theta(x^i))x^i_j\) \(\theta_j' = \theta_j + \alpha\frac1m \sum^m_{i=1}(y^i-h_\theta(x^i))x^i_j\)

      容易得到最优解，但是由于每次考虑所有样本，速度很慢

      \(\alpha\)为学习率

    • 随机梯度下降： \(\theta_j' = \theta_j + \alpha(y^i-h_\theta(x^i))x^i_j\)

      每次找一个样本，迭代速度快，但是不一定每次都朝着收敛的方向

    • 小批量梯度下降法：\(\theta_j' = \theta_j + \alpha\frac1{10} \sum^{i+9}_{k=1}(y^k-h_\theta(x^k))x^k_j\)

      每次更新选择一小部分数据来算，这里面的10可自己选择，数值越大越精确但是慢，越小越快，一般在不影响所用计算机性能的情况下，越大越好；小批量梯度下降法是实际运用中常用的一种方法

  • 梯度下降学习率(步长)：对结果会产生巨大的影响，一般小一些

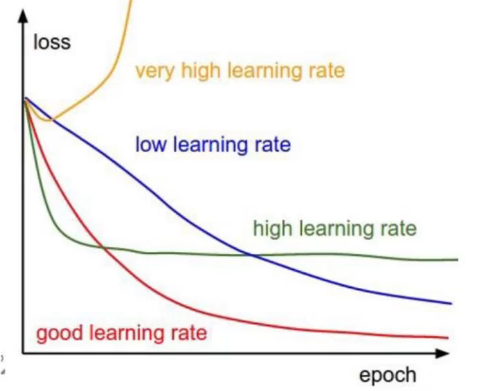
    image-20240102202343315

    • 选择方法：一般从小步长开始，如果结果不好，再变小
    • 批处理数量：通常使用2的幂数作为批量大小，32，64，128都可以，很多时候还得考虑内存和效率