提供二分+DP做法。

Solution

题意

给出 \(n(\le 2\times 10^5)\) 个单调递增偶整数 \(a_i\)，求最小的 \(k\) 满足每一个 \(i\) 都可以在 \(k\) 时刻之前（含）与相邻的数相遇。每个单位时间可以移动一个单位距离。

思路

启发式思考

在想到正解之前，我们可以想想类正解。

显然，在时间一单位一单位过去的时候，一个元素如果愣着不动，肯定不是最优的策略——因为无论它去追随相邻的、或是去相遇相邻的，时间都可以尽可能更优。

所以我们看做元素是不断运动的。

如果它乱走，没有遇到任意一个相邻的元素的情况下，随便改变方向，好像也不优。所以我们也规定一个元素就只有两个阶段：第一、第二阶段——要么先左再右，要么先右再左。

想到这里，对我们有了些许启发。来看看下面这个能拿 80pts 的错解：

就考虑两种情况：

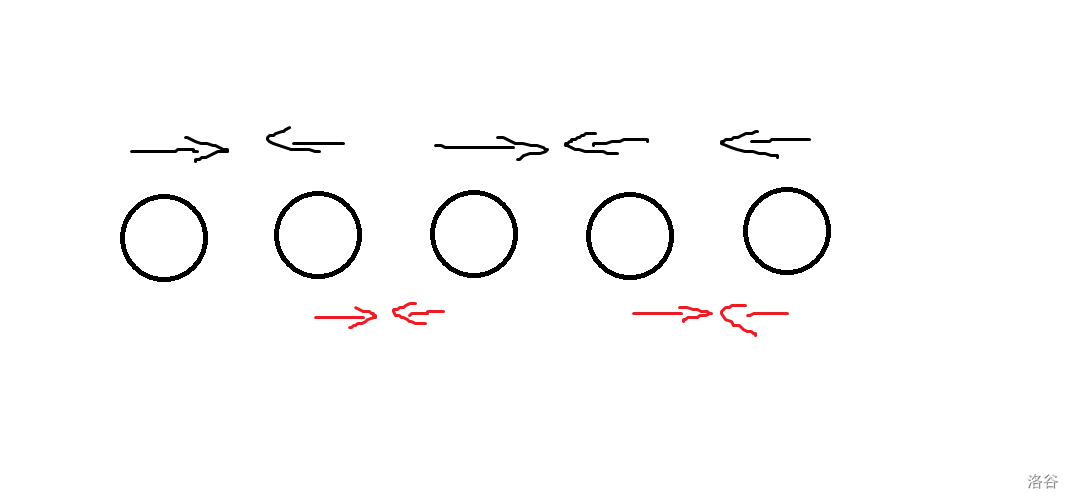
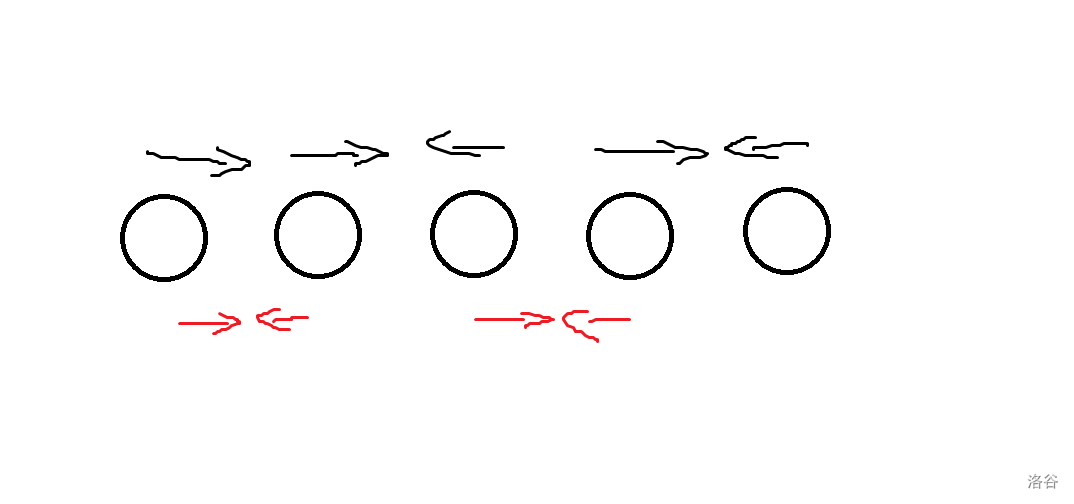
奇（ji）左偶右：黑色表示第一阶段、红色表示第二阶段

奇（ji）右偶左：同上

当然 \(n\) 的奇偶也要考虑。

像这样，是不是以为可以直接 \(O(n)\) 直接跑就解决了？

显然，这太天真了 ~~（像我一样）~~ ，提供一组 hack 数据：

input

10
12 12 24 26 56 70 98 124 124 178

answer

output

至于模拟过程自己模拟吧，这是我能对出来的最小数据了。

贴一个错误代码，可以自己对拍对数据。

正解

我们可以直接二分答案 \(k\)。

接下来考虑怎么扩缩范围。

设 \(f(i,0)\) 表示元素 \(i\) 先左走，调头后最多还可走多少步。

设 \(f(i,1)\) 表示元素 \(i\) 先右走，最多可以走多少步再掉头。

然后就是小学学过的相遇问题，自己在纸上画画就出来了，这里不做赘述。要是不会的话，可以私信。

方程不好整理 ~~（因为我懒）~~ 自己看代码吧。挺具象的。

代码

马蜂抽象就随便看看吧，溜了

code

#include <bits/stdc++.h>
using namespace std;

#define int long long

const int MAXN = 2e5 + 5;

int n;
int a[MAXN];
int d[MAXN];
int f[MAXN][2];

bool check(int md) {
    memset(f, -1, sizeof(f));
    f[1][1] = md;
    for (int i = 2; i <= n; i++) {
        if (f[i - 1][1] != -1) {
            int k = f[i - 1][1];
            if (k - d[i] / 2 >= 0) {
                f[i][0] = max(f[i][0], md - d[i] / 2);
                f[i][1] = max(f[i][1], k - d[i] / 2);
            }
        }
        if (f[i - 1][0] != -1) {
            int k = f[i - 1][0];
            if (k - d[i] / 2 >= 0) {
                f[i][0] = max(f[i][0], k - d[i] / 2);
                f[i][1] = max(f[i][1], k - d[i] / 2);
            }
        }
    }
    return f[n][0] != -1 || f[n][1] != -1;
}

signed main() {
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    for (int i = 2; i <= n; i++) d[i] = a[i] - a[i - 1];
    int l = 1, r = 1e9, mid, ans = -1;
    while (l <= r) {
        mid = l + r >> 1;
        if (check(mid))
            r = mid - 1, ans = mid;
        else
            l = mid + 1;
    }
    printf("%lld\n", ans);
    return 0;
}