得分:228
排名:13
T1:[Usaco2006 Mar]Ski Lift 缆车支柱
题目描述
科罗拉多州的山脉是二维平面上的一条折线。这条折线由 \(N\) 个端点,\(N - 1\) 段线段组成,第 \(i\) 个端点的横坐标就是 \(i\),纵坐标是 \(H_i\),纵坐标代表高度,也可以称为海拔。
罗恩打算为奶牛建造一个滑雪场,为此要在山脉上规划一条缆车线路。缆线也是一条折线,由若干段缆绳组成,起点在山脉的第一个端点,终点在最后一个端点。每段缆绳可以贴着山脉的轮廓,也可以悬浮于空中,跳过山脉上几个海拔低的端点。每段缆绳的水平跨度有限制,不能超过给定的整数 \(K\)。罗恩需要在每段缆绳的端点处修建支柱,用来固定缆绳。
请帮助他规划一下,选择在山脉的哪些端点上修建,才能使得支柱数量最少?注意,根据题意,起点和终点上是一定要修建的。
输入格式
第一行:两个整数 \(N\) 和 \(K\)。第二行到第 \(N + 1\) 行,第 \(i + 1\) 行有一个整数 \(H_i\)。
输出格式
一行一个整数表示最少需要修建的支柱数量。
样例输入
13 4
0
1
0
2
4
6
8
6
8
8
9
11
12
样例输出
5
说明/提示
最优方案是把支柱设在 \(1,5,7,9,13\)。\(5\)不能直接连 \(9\),因为 \(9\) 的海拔较高,\(1\) 不能直接连 \(7\),因为跨度超过了 \(K\)。
数据范围
\(2\le N\le 5000\),\(1\le K\le N-1\),\(H_i\le 10^9\)。
思路
线性 \(DP\)(我就不理解了,为什么线性 \(DP\) 在第一道题呢),主要要考虑两点:
- 两个支柱之间的距离是否大于 \(K\)
- 两个支柱之间的斜率是否大于山的斜率(测试的题面没有洛谷这么良心的说明 \(QAQ\) )
那么考虑倒着练点之后,就可以进行 \(DP\) 了。\(DP\) 方程本身非常简单,就是 \(dp_{i+j}=\min(dp_{i+j},dp_i+1)\)。
die码
#include <bits/stdc++.h>
using namespace std;
int n, k;
int h[5005], dp[500005];
int main() {
memset(dp, 0x3f, sizeof(dp));
cin >> n >> k;
for (int i = 1; i <= n; i++)
cin >> h[i];
dp[1] = 1;
for (int i = 1; i <= n; i++) {
double x = -0x3f3f3f3f;
for (int j = 1; j <= k; j++) {
if (i + j <= n) {
double t = (h[i + j] - h[i]) * 1.0 / (j * 1.0);
if (t >= x) {
dp[i + j] = min(dp[i + j], dp[i] + 1);
x = t;
}
}
}
}
cout << dp[n];
return 0;
}
注意事项:\(x\)作为最小斜率,一定等于\(-0x3f3f3f3f\),如果写成\(x=0\)就会像我一样吃席。
T2:[NOIP2012 普及组] 摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 \(m\) 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 \(n\) 种花,从 \(1\) 到 \(n\) 标号。为了在门口展出更多种花,规定第\(i\)种花不能超过 \(a_i\) 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
输入格式
第一行包含两个正整数 \(n\) 和 \(m\),中间用一个空格隔开。
第二行有 \(n\) 个整数,每两个整数之间用一个空格隔开,依次表示 \(a_1,a_2,⋯,a_n\)。
输出格式
一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对 \(10^6+7\) 取模的结果。
样例输入
2 4
3 2
样例输出
2
数据范围
对于 \(20\%\) 的数据,有 \(0 < n\le 8\),\(0 < m\le 8\),\(0\le a_i\le 8\)。
对于 \(50\%\) 的数据,有 \(0 < n\le 20\),\(0 < m\le 20\),\(0\le a_i\le 20\)。
对于 \(100\%\) 的数据,有 \(0 < n\le 100\),\(0 < m\le 100\),\(0\le a_i\le 100\)。
思路
肥肠简单的背包\(DP\)啊,注意一下 \(k\) 循环条件是 \(\min(j,a_i)\) 即可。
die码
#include<bits/stdc++.h>
using namespace std;
const int mod = 1000007;
int n,m,a[105],dp[105][105];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
dp[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
for(int k=0;k<=min(j,a[i]);k++)
dp[i][j]=(dp[i][j]+dp[i-1][j-k])%mod;
cout<<dp[n][m]<<endl;
return 0;
}
//好好好,比C,D好多了
T3:[NOIP2018 提高组] 货币系统
题目描述
在网友的国度中共有 \(n\) 种不同面额的货币,第 \(i\) 种货币的面额为 \(a_i\),你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 \(n\)、面额数组为 \(a_{1..n}\) 的货币系统记作 \((n,a)\)。
在一个完善的货币系统中,每一个非负整数的金额 \(x\) 都应该可以被表示出,即对每一个非负整数 \(x\),都存在 \(n\) 个非负整数 \(t_i\) 满足 \(a_i\times t_i\) 的和为 \(x\)。然而,在网友的国度中,货币系统可能是不完善的,即可能存在金额 \(x\) 不能被该货币系统表示出。例如在货币系统 \(n=3,a=[2,5,9]\) 中,金额 \(1,3\) 就无法被表示出来。
两个货币系统 \((n,a)\) 和 \((m,b)\) 是等价的,当且仅当对于任意非负整数 \(x\),它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 \((m,b)\),满足 \((m,b)\) 与原来的货币系统 \((n,a)\) 等价,且 \(m\) 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 \(m\)。
输入格式
输入文件的第一行包含一个整数 \(T\),表示数据的组数。
接下来按照如下格式分别给出 \(T\) 组数据。每组数据的第一行包含一个正整数 \(n\)。接下来一行包含 \(n\) 个由空格隔开的正整数 \(a[i]\)。
输出格式
输出文件共有 \(T\) 行,对于每组数据,输出一行一个正整数,表示所有与 \((n,a)\) 等价的货币系统 \((m,b)\) 中,最小的 \(m\)。
样例输入
2
4
3 19 10 6
5
11 29 13 19 17
样例输出
2
5
说明/提示
在第一组数据中,货币系统 \((2,[3,10])\) 和给出的货币系统 \((n,a)\) 等价,并可以验证不存在 \(m<2\) 的等价的货币系统,因此答案为 \(2\)。在第二组数据中,可以验证不存在 \(m < n\) 的等价的货币系统,因此答案为 \(5\)。
数据范围
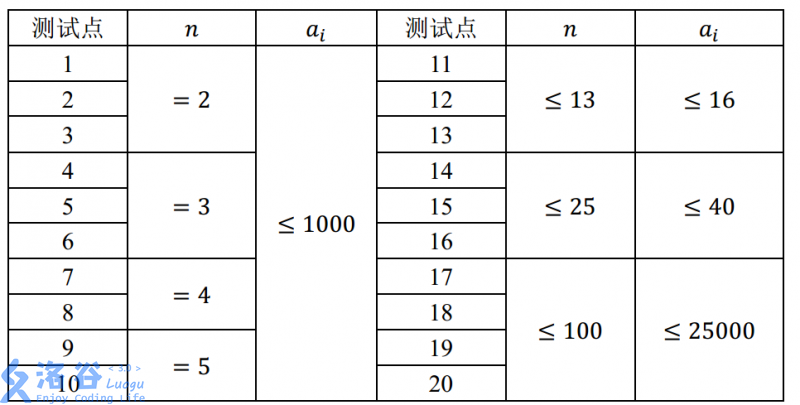
对于 \(100\%\) 的数据,满足 \(1\le T\le 20\),\(n,a_i\ge 1\)。
思路
思路很简单,简化一个货币系统,其实就是把能用别的面额表示出来的面额去掉,剩下的不能用别的面额表示的面额,就是必须留下来的面额。
\(DP\) 方程:\(dp_j=\max(dp_j,dp_{j-a_i}+1)\)。
die码
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
int T;
int main() {
cin >> T;
for (int q = 1; q <= T; q++) {
int n, m = 0, ans = 0;
int a[105], dp[211314];
memset (dp, -0x3f, sizeof(dp));
dp[0] = 0;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
m = max(m, a[i]);
}
for (int i = 1; i <= n; i++)
for (int j = a[i]; j <= m; j++)
dp[j] = max(dp[j], dp[j - a[i]] + 1);
for (int i = 1; i <= n; i++)
if (dp[a[i]] == 1)
ans++;
cout << ans << endl;
}
return 0;
}
注意事项:不要试图特判 \(2\) 之类的数据骗分,因为这本来是可以 \(AC\) 的,只是因为特判,我得了 \(85\)。
T4:Two Arrays
题目描述
You are given two integers \(n\) and \(m\) . Calculate the number of pairs of arrays \((a,b)\) such that:
the length of both arrays is equal to \(m\) ;
each element of each array is an integer between \(1\) and \(n\) (inclusive);
\(a_i\le b_i\) for any index \(i\) from \(1\) to \(m\) ;
array \(a\) is sorted in non-descending order;
array \(b\) is sorted in non-ascending order.
As the result can be very large, you should print it modulo \(10^9+7\) .
输入格式
The only line contains two integers \(n\) and \(m\) ( \(1\le n\le 1000\) , \(1\le m\le 10\) ).
输出格式
Print one integer – the number of arrays \(a\) and \(b\) satisfying the conditions described above modulo \(10^9+7\) .
题意翻译
输入两整数 \(n\)、\(m\),求有多少对正整数序列 \(a_i\)、\(b_i\)满足:
\(a_i\)、\(b_i\) 的长度为 \(m\);
\(a_i\)、\(b_i\) 中所有元素的值小于等于 \(n\);
对于所有 \(1\le i\le m\),\(a_i\le b_i\);
序列 \(a\) 单调不降,序列 \(b\) 单调不升。
答案对 \(10^9+7\) 取模。
思路
die码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
int n, m;
ll dp[25][1005], sum[25][1005];
int main() {
cin >> n >> m;
m *= 2;
for (int i = 1; i <= n; i++) {
dp[1][i] = 1;
sum[1][i] = i;
}
for (int i = 2; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = sum[i - 1][j];
sum[i][j] = ((sum[i][j - 1] + dp[i][j]) % mod + mod) % mod;
}
}
ll ans = 0;
for (int i = 1; i <= n; i++)
ans = ((ans + dp[m][i]) % mod + mod) % mod;
cout << ans;
return 0;
}