问题描述
问题背景:
输入法自动更正:当我们输入了一个不正确的词时,输入法就可能自动给我们更正。例如下面的例子:
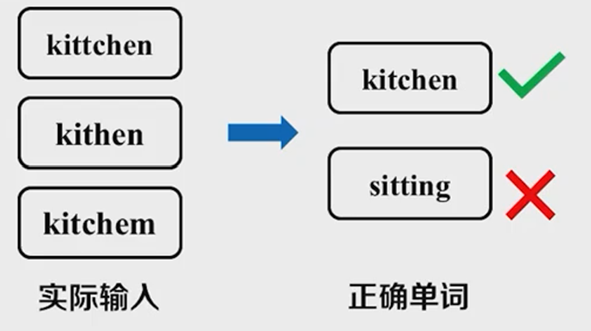

图 1
提出问题:为什么输入法能够选到正确的那个词呢?
我们的猜想是,可能输入法会找“长得像”的词作为他推荐给用户的,也就是更正的词。那么如何让计算机知道什么叫长得像呢?具体来讲,如何衡量字符串之间的相似程度呢?
问题分析
相似操作的衡量可以用编辑距离来作为标准。
编辑距离是指又称Levenshtein距离(莱文斯坦距离也叫做Edit Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
它可以用来做DNA分析,拼字检测,抄袭识别等等。总是比较相似的,或多或少我们可以考虑编辑距离。
在概念中,我们可以看出一些重点那就是,编辑操作只有三种。插入,删除,替换这三种操作,我们有两个字符串,将其中一个字符串经过上面的这三种操作之后,得到两个完全相同的字符串付出的代价是什么就是我们要讨论和计算的。
比如上面的例子中,如果左侧的词想要变成“kitchen”,只需要进行一次编辑操作。
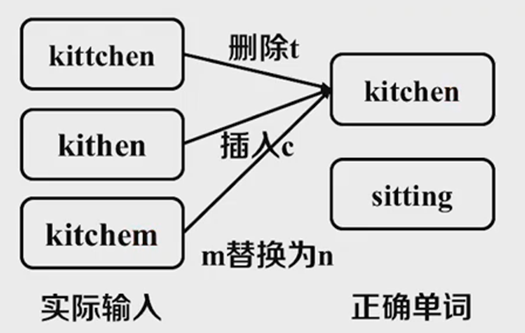
图 2
而想要变成“setting”就要进行更多的编辑操作。

图 3
这里,我们将编辑操作的次数叫做编辑距离。
然而,我们可以将一个词插入再将这个词删除,如此反复,进而他的编辑距离将无限大。因此,寻找最大编辑距离是没有太大意义的,我们要探究的是最小编辑距离。
算法过程描述
最小编辑距离的定义:
输入:长度为n的字符串s,长度为m的字符串t
输出:求出一组编辑操作O = < e1 , e2 , e3 , …… ed >,令 min|O |
字符串s经过O的操作后满足s = t
给出问题表示:
我们假设D[i,j]为字符串s[1…i]变为t[1…j]的最小编辑距离
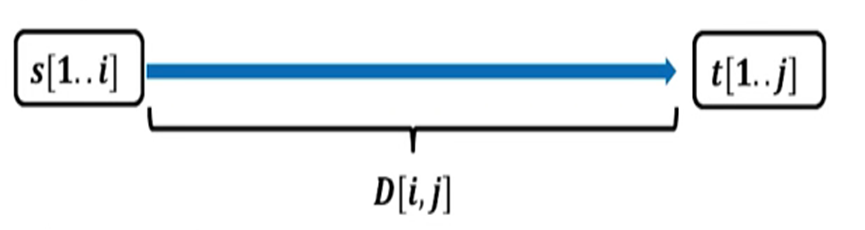
图 4
递推关系的建立:
分析最优结构:
考察末尾元素:删除
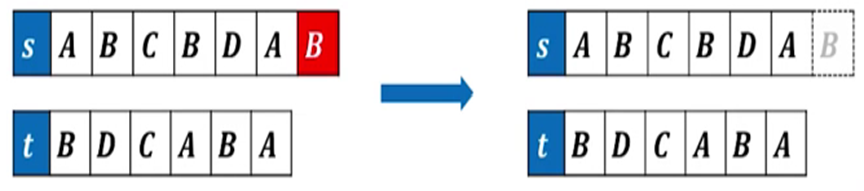
图 5
删除操作,把s串的最后一位删掉,此时的子问题是寻找D[i-1,j]的值
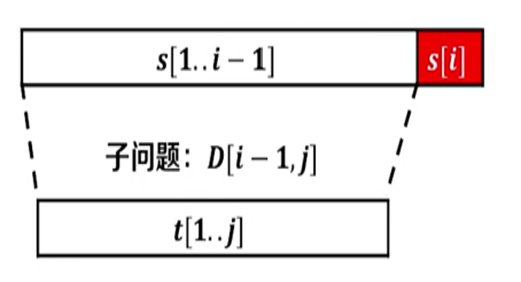
图 6
此时我们所求的D[i,j]应该等于其子问题的 D[i-1,j]加上本身进行的删除操作。
进而我们得到递推关系式D[i,j] = D[i-1,j] + 1
考察末尾元素:插入
插入操作:在s字符串目前最后一位的后面插入一个字符,这个值应该是t字符串的最后一个字符。
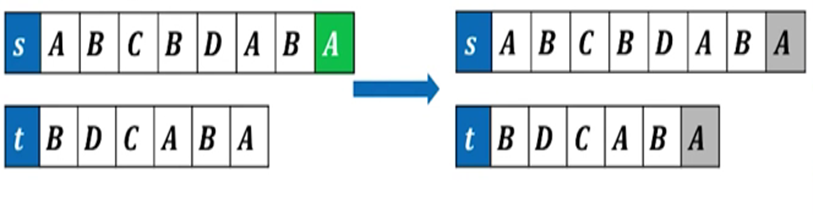
图 7
此时我们所求的D[i,j]应该等于其子问题的 D[i,j-1]加上本身进行的插入操作。
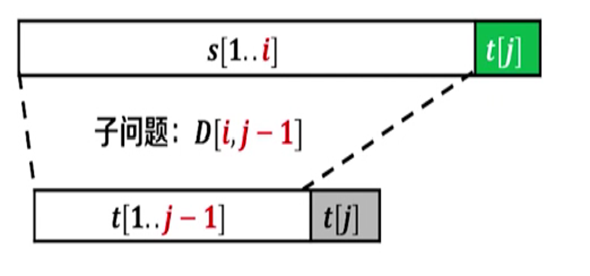
图 8
进而我们得到递推关系式D[i,j] = D[i,j-1] + 1
考察末尾元素:替换
替换操作:在s字符串目前最后一位替换成其他的一个字符,这个字符应该是t字符串的最后一个字符。
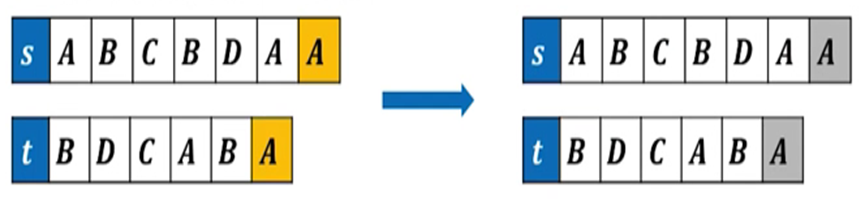
图 9
如果是s[i] = t[i],则不需要替换,否则需要替换。
当需要替换的时候,我们所求的D[i,j]应该等于其子问题的 D[i-1,j-1]加上本身进行的替换操作。
当不需要替换的时候,我们所求的D[i,j]应该等于其子问题的 D[i-1,j-1]
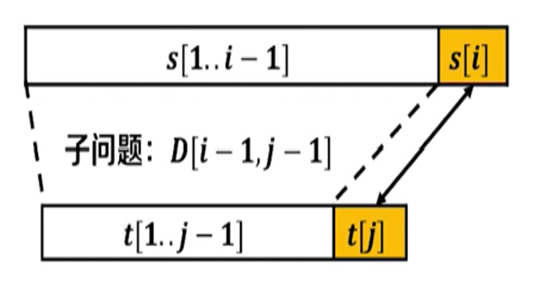
图 10
进而我们得到递推关系式
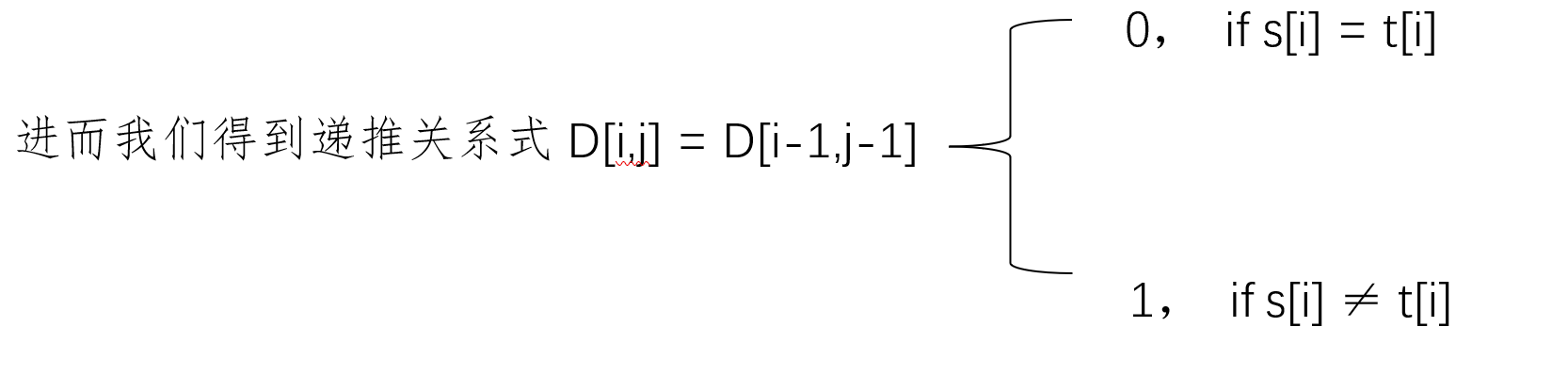
构造递推公式:
综上所述,可以将上述总结为如下递推公式:
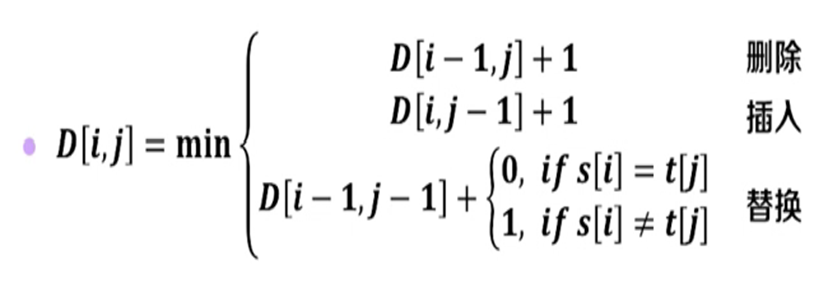
图 11
自底向上计算:
初始化:
D[i,0] = i 表示把长度为i的串变为空串至少需要i次操作。
D[0,j] = j 表示把长度为0的串变为长度为j串至少需要j次操作。
于是我们可以得到这样一张表:
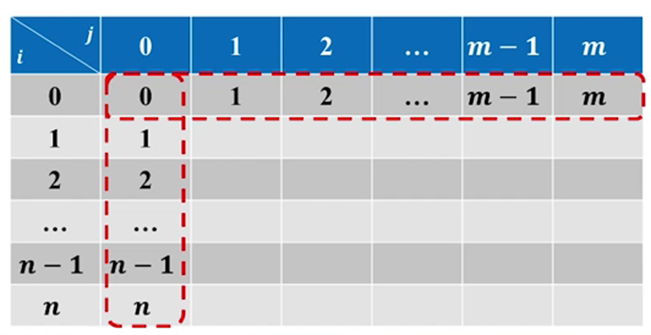
图 12
递推公式:
根据前面推导出的递推公式,我们就可以得知每个位置的内容应该是什么。

图 13
最优方案:
记录过程:
我们需要使用新的一个二维数组Rec用来记录每次选择的操作。
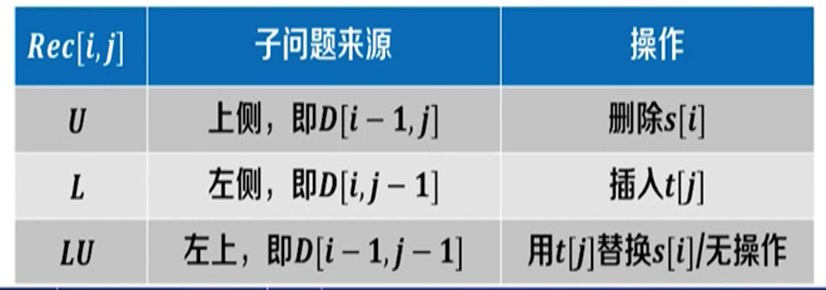
图 14
上表说明:
如果Rec[i,j] = U 则说明进行的是删除操作
如果Rec[i,j] = L 则说明进行的是插入操作
如果Rec[i,j] = LU 则说明进行的是替换操作或者无操作
最后我们得到这样一个Rec二维数组:
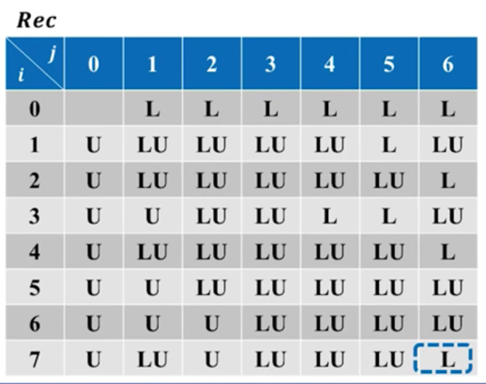
图 15
过程回溯:
现在我们需要根据Rec二维数组来给出我们把s串变为t串所需要的步骤。
从D[i][j]位置开始回溯:
如果当前位置为”L”:
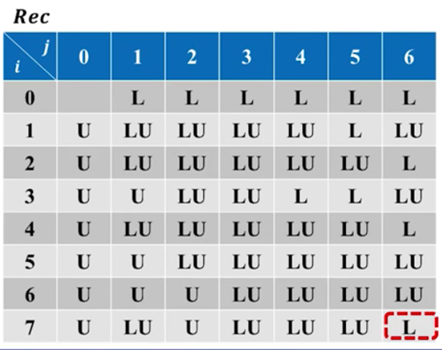
图 16
则下一个位置应该变为Rec[i][j-1],意味着此s[i]应该插入t[j],而这一步的上一步,t的长度为j-1,最优操作为Rec[i][j-1]。
如果当前位置为”U”:
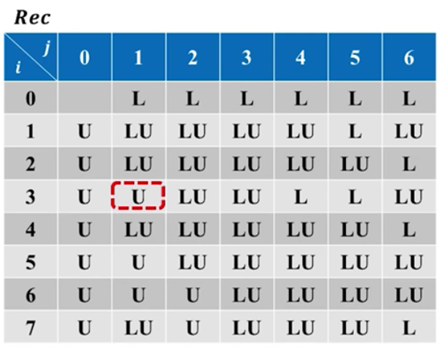
图 17
则下一个位置应该变为Rec[i-1][j],意味着此s[i]应该删除,而这一步的上一步,s的长度为i-1,最优操作为Rec[i-1][j]。
如果当前位置为”LU”:
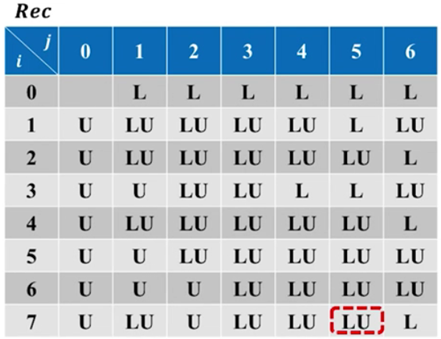
图 18
则下一个位置应该变为Rec[i-1][j-1],意味着此s[i]应该被替换为t[j]或者不变,而这一步的上一步,s的长度为i-1,t的长度为j-1,最优操作为Rec[i-1][j-1]。
算法复杂度分析
算法的伪代码:
MinDistance(s,t) //求s和t的最小编辑距离 //输入:字符串s和t //输出:s和t的最小编辑距离 新建D[0...n][0...m],Rec[0...n][0...m]两个二维数组 n ← length(s) m ← length(t) //初始化 for i ← 0 to n do D[i,0] ← i Rec[i,0] ← ‘U’ for j ← 0 to m do D[0,j] ← j Rec[i,0] ← ‘L’ //动态规划 for i ← 0 to n do for j ← 0 to m do c ← 0 if si ≠ tj then c ← 1 replace ← D[i - 1 ,j - 1]+ c delete ← D[i - 1 ,j ]+ 1 insert ← D[i ,j - 1] + 1 if replace = min{delete,insert,replace} then D[i ,j ] ← D[i - 1 ,j - 1] + c Rec[i ,j ] ← “LU” else if insert = min{delete,insert,replace} then D[i ,j ] ← D[i ,j - 1] + 1 Rec[i ,j ] ← “L” else D[i ,j ] ← D[i - 1,j] + 1 Rec[i ,j ] ← “U” (Rec,s,t,n,m) //寻找最优方案并输出 //输入:二维数组Rec,字符串s,t,位置下标n,m //输出:操作序列 if n = 0 and m = 0 then return if Rec[n,m] = “LU” then PrintMinDistance(Rec,s,t,n-1,m-1) if sn = tm then print “无操作” else print “用tm替换sn” else if Rec[n,m] = “U” then PrintMinDistance(Rec,s,t,n-1,m) print”删除sn” else PrintMinDistance(Rec,s,t,n,m-1) print”插入tm”
算法时间复杂度分析:
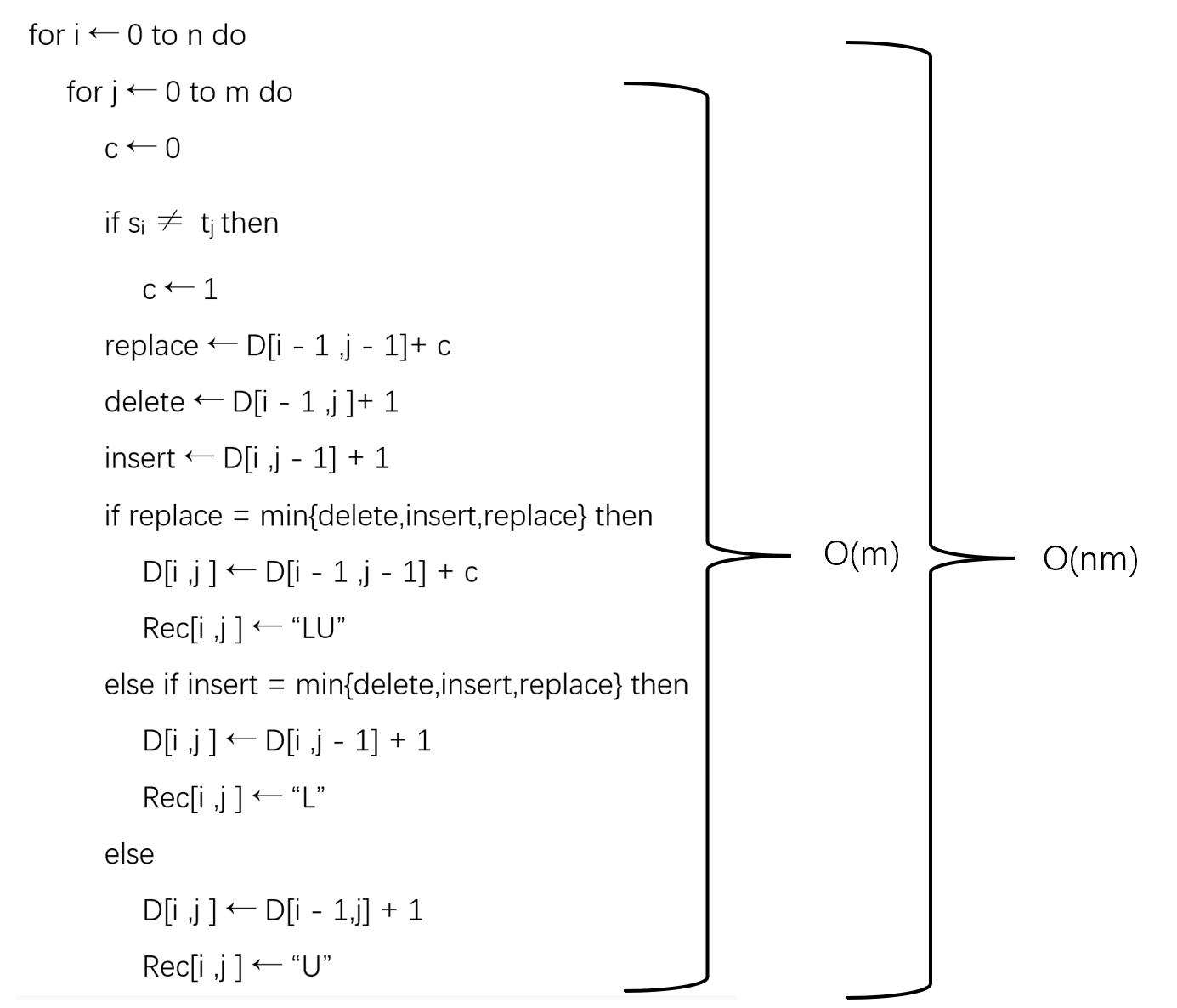
图 19
可以看出,整个算法的核心算法是动态规划,而动态规划使用了两个for循环来遍历二维数组的每个位置,所以其时间复杂度为O(nm)
算法改进
原来的算法是创建一个大小为s*t的矩阵。如果所有字符串加起来是1000个字符那么长的话,那么这个矩阵就会是1M。
对于计算编辑距离,如果我们不需要回溯,而是只想知道两者的最小编辑距离,那么上面的算法存储空间就是可以改进的,仔细观察你会发现递推公式的计算过程以及距离矩阵,你会发现当前距离的计算只和前一行以及当前行有关,即每次计算都只需要斜向的[i-1,j-1]、横向的[i,j-1]和纵向的[i-1,j]。而我们现在不需要知道中间结果,只需要最终结果,那么可以只要两行存储空间,进行迭代计算即可。现在只需要cur_row[]和pre_row[]两个一维数组即可。
现在的算法版本只使用2*t个元素。其结果是,不但内存占用更少,而且速度也变快了!因为这使得内存分配只需要很少的时间来完成。当两个字符串的长度都是1k左右时,新算法的效率是旧算法的两倍!
MinDistance_2(s,t) //求s和t的最小编辑距离 //输入:字符串s和t //输出:s和t的最小编辑距离 新建cur_row [0...n],pre_row [0...n]两个一维数组 m ← length(s) n ← length(t) //初始化 for i ← 0 to n do pre_row [i] ← i //动态规划 for i ← 0 to m do cur_row [0] ← i for j ← 0 to n do c ← 0 if si ≠ tj then c ← 1 replace ← D[i - 1 ,j - 1]+ c delete ← D[i - 1 ,j ]+ 1 insert ← D[i ,j - 1] + 1 if replace = min{delete,insert,replace} then cur_row [j] ← pre_row [j-1]+ c else if insert = min{delete,insert,replace} then cur_row [j]← cur_row [j-1]+ 1 else cur_row [j] ← pre_row [j-1]+ 1 swap(cur_row, pre_row) return pre_row[n]
实验分析
实验结果:
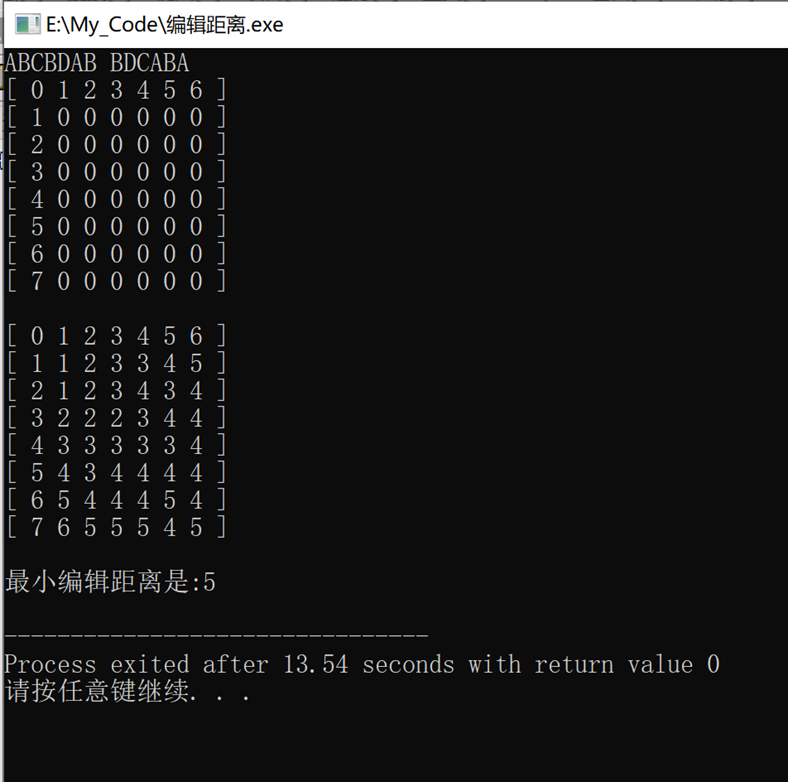
图 20
|
为了方便记录,我将Rec数组设置为int型, 其中 1 表示 “插入” = L 2 表示 “删除” = U 3 表示 “替换/无操作” = LU 通过人工进行验证,证明其操作步骤是正确的。 根据Rec数组记录的数据,我们就可以输出当前位置时进行的操作。由于查找步骤的算法是通过递归实现的,所以当输出时,就是按照正常的顺序来的。 |
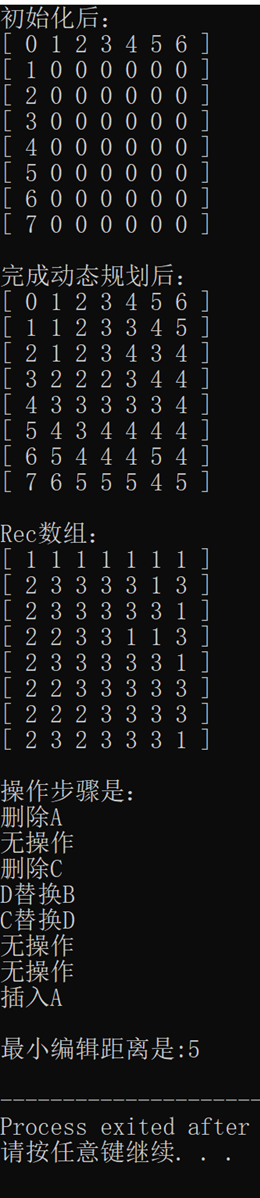
图 21
实验分步分析:
初始化:
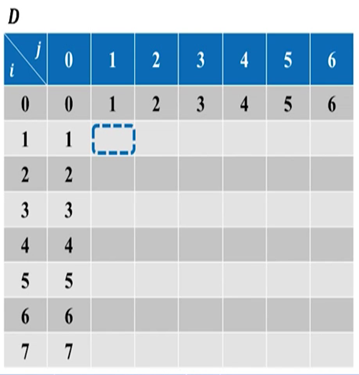
图 22

进行递归:
以D[1,1]举例:
- 如果是删除操作,则D[1,1] = D[0,1] + 1 = 2
- 如果是插入操作,则D[1,1] = D[1,0] + 1 = 2
- 如果是替换操作,先判断s[i] 和 t[i] 是否相同,不相同则D[1,1] = D[0,0] + 1 = 1
可见最小为1,则D[1,1] = 1
如果这三种操作后编辑距离相同,则优先选择替换操作。
最终会得到这样两个个表:
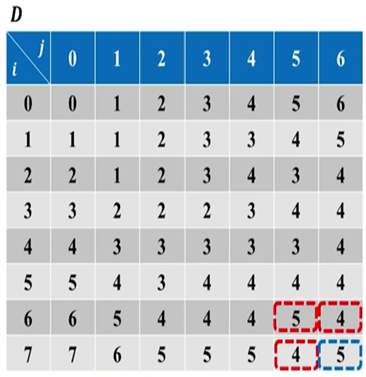


图 23
则最后D[i][j]就为最优解。
算法对比:
运行时间采集方式:
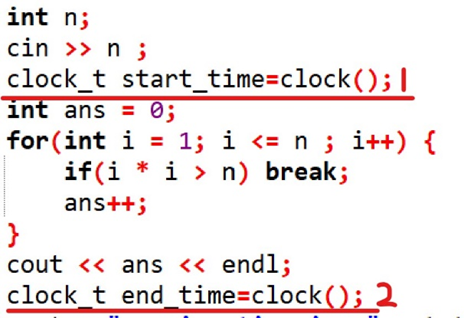
图 24
使用系统自带函数clock(),这个函数返回从“开启这个程序进程”到“程序中调用clock()函数”时之间的CPU时钟计时单元数。在程序开始时先记录一个时钟数,在程序结束时再记录一个时钟数。将两个时钟数相减并除以一秒钟内CPU运行的时钟周期数(宏定义为CLOCKS_PER_SEC)就能得到程序运行时间。
测试数据规模:
8组随机字符串。
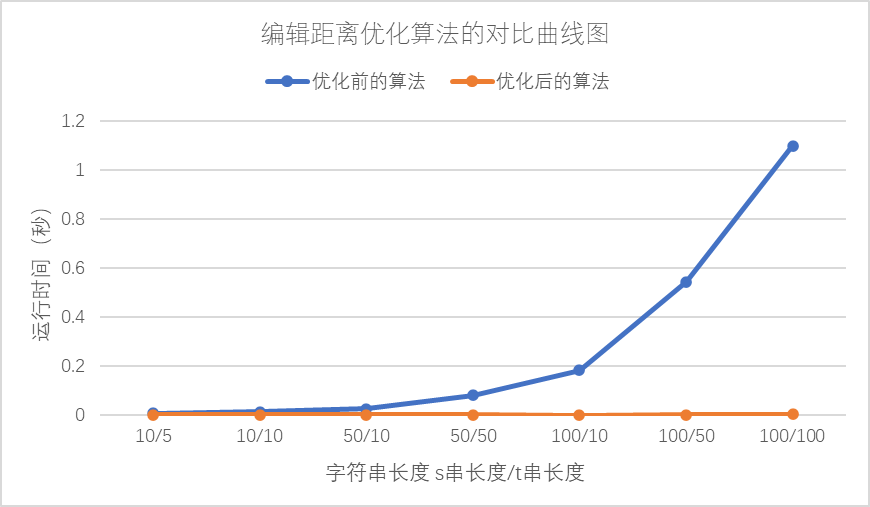
|
表 1 |
从图中我们可以看出,优化的算法显然更快。但由于算法执行过程中需要进行当前D二维数组的输出,所以越大的数组占用的时间输出的时间越长。排除输出的干扰,我们发现其实优化前后的执行时间并没有图中那样差距,单从算法的执行时间来说,两种算法基本相同。但是后一种占用空间更小。
参考文献:
clayyjh. C语言 记录程序的执行时间[EB/OL] [2021-03-12].
https://www.cnblogs.com/clayyjh/p/14526665.html
小乔流水人家. C语言 查看运行程序所需要的时间和占用的内存[EB/OL] [2017-02-22].
https://www.cnblogs.com/BeautyFuture/articles/6428551.html
Penny呀 Levenshtein编辑距离算法的改进---剪枝优化 [EB/OL] [ 2021-01-17]. https://blog.csdn.net/PennyYu123/article/details/112747791
程序员的自我反思 经典动态规划问题:最短编辑距离算法的原理及实现 [EB/OL] [ 2019-04-04].
https://blog.csdn.net/a553181867/article/details/89008264
May Hacker 最小编辑代价(编辑距离问题改进版) [EB/OL] [ 2021-05-29]. https://blog.csdn.net/weixin_43889841/article/details/117381508
附录:
#include<bits/stdc++.h> using namespace std; int D[100][100]; int Rec[100][100]; char str1[100] = "ABCBDAB", str2[100] = "BDCABA"; int min(int a, int b, int c) { int temp = a < b ? a : b; return temp < c ? temp : c; } void print1(int n,int m) { for(int i = 0 ; i < n ; i++) { cout << "[ "; for(int j = 0 ; j < m ; j++) { cout << D[i][j] << ' '; } cout << "]" << endl; } cout << endl; } void print2(int n,int m) { for(int i = 0 ; i < n ; i++) { cout << "[ "; for(int j = 0 ; j < m ; j++) { cout << Rec[i][j] << ' '; } cout << "]" << endl; } cout << endl; } void PrintMinDistance(int n,int m) { if(n == 0 && m == 0) return; if(Rec[n][m] == 3) { PrintMinDistance(n-1,m-1); if(str1[n-1] == str2[m-1]) { cout << "无操作" << endl; } else { cout << str2[m-1] << "替换" << str1[n-1] << endl; } } else if(Rec[n][m] == 2) { PrintMinDistance(n-1,m); cout << "删除" << str1[n-1] << endl; } else { PrintMinDistance(n,m-1); cout << "插入" << str2[m-1] << endl; } } int MinDistance(char str1[], char str2[]) { int i, j, len1, len2; len1 = strlen(str1); len2 = strlen(str2); //初始化 for(i = 0; i <= len1; i++) { D[i][0] = i; Rec[i][0] = 2; } for(j = 0; j <= len2; j++) { D[0][j] = j; Rec[0][j] = 1; } cout << "初始化后:" << endl; print1(i,j); //动态规划 for(i = 1; i <= len1; i++) for(j = 1; j <= len2; j++) { if(str1[i - 1] == str2[j - 1]) { //因为D比str1和str2多了第0行和第0列,str是从下标0开始存数,而D[]是从下标1才开始真正存数,所以D[i]对应str[i - 1], 里一定要注意。 D[i][j] = D[i - 1][j - 1]; Rec[i][j] = 3; } else { int insert = D[i][j - 1] + 1; int dele = D[i - 1][j] + 1; int replace = D[i - 1][j - 1] + 1; D[i][j] = min(insert, dele, replace); if(D[i][j] == replace) Rec[i][j] = 3; else if(D[i][j] == insert ) Rec[i][j] = 1; else Rec[i][j] = 2; } } cout << "完成动态规划后:" << endl; print1(i,j); cout << "Rec数组:" << endl; print2(i,j); cout << "操作步骤是:" << endl; PrintMinDistance(len1,len2); cout << endl; return D[len1][len2]; } int main() { // cin >> str1 >> str2; printf("最小编辑距离是:%d\n", MinDistance(str1, str2)); }