密码学复习笔记
欧几里得算法
欧几里得算法 (辗转相除法)利用带余除法求两个整数a和b的最大公因子的过程。
给定两个正整数a和b,假定a大于b,由带余除法,可以得到:其中r就是a和b的最大公因子



算术基本定理

同余关系的性质

取模重要结论
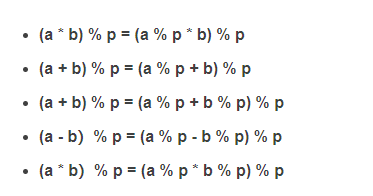

快速模幂运算
如果B是2的幂,我们如何快速计算 A^B mod C
使用模乘法规则:
例如 A^2 mod C = (A * A) mod C = ((A mod C) * (A mod C)) mod C
我们可以用此来快速计算 7^256 mod 13
7^1 mod 13 = 7
7^2 mod 13 = (7^1 *7^1) mod 13 = (7^1 mod 13 * 7^1 mod 13) mod 13
我们可以把之前 7^1 mod 13 的结果 代入 这个方程式。
7^2 mod 13 = (7 *7) mod 13 = 49 mod 13 = 10
7^2 mod 13 = 10
7^4 mod 13 = (7^2 *7^2) mod 13 = (7^2 mod 13 * 7^2 mod 13) mod 13
我们可以把之前 7^2 mod 13 的结果 代入 这个方程式。
7^4 mod 13 = (10 * 10) mod 13 = 100 mod 13 = 9
7^4 mod 13 = 9
7^8 mod 13 = (7^4 * 7^4) mod 13 = (7^4 mod 13 * 7^4 mod 13) mod 13
我们可以把之前 7^4 mod 13 的结果 代入 这个方程式。
7^8 mod 13 = (9 * 9) mod 13 = 81 mod 13 = 3
7^8 mod 13 = 3
以这种方式继续,将先前的结果代入我们的等式中。
...在5个迭代之后可以得到:
7^256 mod 13 = (7^128 * 7^128) mod 13 = (7^128 mod 13 * 7^128 mod 13) mod 13
7^256 mod 13 = (3 * 3) mod 13 = 9 mod 13 = 9
7^256 mod 13 = 9
只要 B 是 2 的幂,我们就有一个快速计算 A^B mod C 的方法。
然而,如果 B 不是 2 的幂,我们也需要一种快速模乘法的方法。
如果 B是任何数,我们如何快速计算 A^B mod C?

步骤1:将B记录为二进制形式,使其成为2的幂

从最右边的数字开始,让k = 0 并且 为 每个数字:
- 如果数字为1,我们需要一个2^k的部分,否则我们不需要
- 将 1 加到 k,然后向左移动到下一个数

步骤 2:计算 ≤ B 的 2 的幂 mod C
5^1 mod 19 = 5
5^2 mod 19 = (5^1 * 5^1) mod 19 = (5^1 mod 19 * 5^1 mod 19) mod 19
5^2 mod 19 = (5 * 5) mod 19 = 25 mod 19
5^2 mod 19 = 6
5^4 mod 19 = (5^2 * 5^2) mod 19 = (5^2 mod 19 * 5^2 mod 19) mod 19
5^4 mod 19 = (6 * 6) mod 19 = 36 mod 19
5^4 mod 19 = 17
5^8 mod 19 = (5^4 * 5^4) mod 19 = (5^4 mod 19 * 5^4 mod 19) mod 19
5^8 mod 19 = (17 * 17) mod 19 = 289 mod 19
5^8 mod 19 = 4
5^16 mod 19 = (5^8 * 5^8) mod 19 = (5^8 mod 19 * 5^8 mod 19) mod 19
5^16 mod 19 = (4 * 4) mod 19 = 16 mod 19
5^16 mod 19 = 16
5^32 mod 19 = (5^16 * 5^16) mod 19 = (5^16 mod 19 * 5^16 mod 19) mod 19
5^32 mod 19 = (16 * 16) mod 19 = 256 mod 19
5^32 mod 19 = 9
5^64 mod 19 = (5^32 * 5^32) mod 19 = (5^32 mod 19 * 5^32 mod 19) mod 19
5^64 mod 19 = (9 * 9) mod 19 = 81 mod 19
5^64 mod 19 = 5
步骤3:使用模乘法属性来组合已算出的 mod C 的值
5^117 mod 19 = ( 5^1 * 5^4 * 5^16 * 5^32 * 5^64) mod 19
5^117 mod 19 = ( 5^1 mod 19 * 5^4 mod 19 * 5^16 mod 19 * 5^32 mod 19 * 5^64 mod 19) mod 19
5^117 mod 19 = ( 5 * 17 * 16 * 9 * 5 ) mod 19
5^117 mod 19 = 61200 mod 19 = 1
5^117 mod 19 = 1
来源:快速模幂运算